
Empirical probability Formula , also known as experimental probability, is a probability measurement derived from historical or observed data. In simpler terms, it represents the likelihood of an event happening based on past observations. In contrast, theoretical probability assumes equal likelihood for all events and predicts probabilities accordingly.
The Empirical probability Formula involves multiplying the number of times a specific event occurs by the total number of trials. To clarify further, probability can be categorized as either theoretical probability or empirical probability.
What Is Empirical Probability Formula?
Empirical probability Formula is determined by what has occurred in actual observations or experiments. In contrast, theoretical probability aims to predict outcomes based on the total number of possible events. As the number of trials in an experiment increases, we typically anticipate that the experimental and theoretical probabilities will converge and become very close to each other.
The Empirical probability Formula is not provided in your text, but I can clarify that it is often calculated by dividing the number of favorable outcomes (events of interest) by the total number of trials or observations. The formula can be written as:
Empirical Probability Formula = Number of Favorable Outcomes / Total Number of Trials or Observations
Empirical Probability Formula = f/n
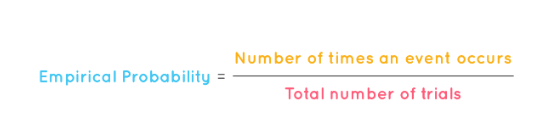
where,
- f is the number of times an event occurs
- n is the total number of trials
This formula allows us to estimate the probability of an event based on empirical or observed data.
Empirical Probability Formula Definition
Empirical probability Formula, often referred to as experimental probability or relative frequency, is a probability estimation method derived from real-world experiences and observations. Unlike theoretical probability, empirical probability formula does not rely on assumptions or hypotheses. Instead, it is grounded in concrete experimental studies and observed data. This makes it a valuable approach for estimating probabilities based on real-life outcomes and events.
Difference Between Empirical Probability Formula and Theoretical Probability Formula.
empirical probability formula and theoretical probability are two distinct approaches to calculating probabilities in statistics and probability theory. Here are the key differences between them:

Basis of Calculation:
- Empirical Probability: This is based on real-world observations and data. It is calculated by counting the actual occurrences of an event in a series of trials or experiments.
- Theoretical Probability: This is based on theoretical assumptions about the likelihood of events. It is calculated by considering all possible outcomes and their associated probabilities.
Data vs. Assumptions:
- Empirical Probability: It does not rely on assumptions or theoretical models. It uses observed data to estimate probabilities.
- Theoretical Probability: It relies on theoretical assumptions and models, assuming that all outcomes are equally likely unless stated otherwise.
Calculation Method:
- Empirical Probability Formula: It is calculated by dividing the number of favorable outcomes (events of interest) by the total number of trials or observations.
- Theoretical Probability Formula : It is calculated using mathematical formulas and principles, often based on the assumption of equally likely outcomes.
Applicability:
- Empirical Probability Formula: Typically used when you have real-world data or observations, making it suitable for situations where theoretical probabilities are hard to determine.
- Theoretical Probability Formula: Applied in situations where you have a clear understanding of the underlying probabilities, such as in games of chance with known rules.
Variability:
- Empirical Probability Formula: It can vary from one set of observations to another, depending on the actual outcomes of the trials or experiments.
- Theoretical Probability Formula: It remains constant and does not change based on observations since it is based on theoretical assumptions.
Example:
- Empirical Probability Formula: If you toss a fair coin 100 times and count the number of times it lands heads, the empirical probability of getting heads would be based on the actual outcomes.
- Theoretical Probability Formula: In the case of a fair coin, the theoretical probability of getting heads is 0.5 (50%) because it assumes that heads and tails are equally likely outcomes.
In summary, empirical probability formula is grounded in real-world data and observations, while theoretical probability is based on mathematical models and assumptions about probabilities. The choice between the two depends on the nature of the problem and the availability of data or theoretical understanding.
Empirical Probability Formula Advantages
- Free from Hypotheses: Empirical probability does not rely on assumptions or hypotheses about the data. It is based on observed data, making it a more data-driven approach.
- No Assumptions About Data: Unlike theoretical probability, which often assumes equally likely outcomes, empirical probability makes no such assumptions. It derives probabilities directly from observed frequencies.
- Backed by Experimental Studies and Data: Empirical probability is grounded in real-world experimental studies and observed data, making it a practical and applicable approach.
- Covers More Cases than Classical Probability: Empirical probability is versatile and can be applied to situations where classical or theoretical probability may not be appropriate due to unequal or unknown probabilities of events.
- Applicable When Outcomes Are Not Equally Likely: Empirical probability is particularly useful when outcomes are not equally likely, as it directly reflects the observed frequencies of events, regardless of their theoretical probabilities.
Empirical Probability Formula Disadvantages
- Large Sample Sizes Needed: To obtain reliable estimates of probabilities through empirical probability formula, larger sample sizes are generally preferred. Larger samples reduce the impact of random variations and lead to more accurate estimations.
- Reduced Accuracy with Small Sample Sizes: Smaller sample sizes can result in less accurate probability estimates due to the increased influence of random fluctuations.
- Potential for Incorrect Solutions: In cases with very small sample sizes, there's a higher risk of drawing incorrect conclusions or making inaccurate predictions about probabilities.
- Impossibility of Infinite Repeats: While theoretical probability assumes an infinite number of repetitions to establish probabilities, this is physically impossible in many real-world scenarios. Empirical probability doesn't require infinite repetitions but still relies on sufficiently large samples for accuracy.
- Divergence from Classical Probability: Empirical probability doesn't always align with classical probability, especially when the assumptions of classical probability (e.g., equally likely outcomes) do not hold in the observed data. It provides a more practical and data-driven perspective.
Empirical Probability Formula Examples
Example 1: In a deck of 52 playing cards, you draw a card at random. What is the empirical probability of drawing a spade?
Solution:
Number of favorable outcomes (spades) = 13 (there are 13 spades in a deck).
Total number of possible outcomes (cards in a deck) = 52.
Empirical Probability = (Number of Spades) / (Total Number of Cards) = 13 / 52 = 0.25 or 25%.
Therefore, the empirical probability of drawing a spade is 0.25, or 25%.
Example 2: In a class of 30 students, 20 students passed a math test. What is the empirical probability of a randomly selected student passing the math test?
Solution:
Number of favorable outcomes (students who passed) = 20.
Total number of students = 30.
Empirical Probability = (Number of Students Who Passed) / (Total Number of Students) = 20 / 30 = 2/3 = 0.6667 or approximately 66.67%.
Therefore, the empirical probability of a randomly selected student passing the math test is approximately 66.67%.
Example 3: In a jar of 100 marbles, 30 are red, 40 are blue, and 30 are green. What is the empirical probability of drawing a blue marble?
Solution:
Number of favorable outcomes (blue marbles) = 40.
Total number of marbles = 100.
Empirical Probability = (Number of Blue Marbles) / (Total Number of Marbles) = 40 / 100 = 0.4 or 40%.
Therefore, the empirical probability of drawing a blue marble is 0.4, or 40%.
These examples illustrate how to calculate empirical probability by dividing the number of favorable outcomes by the total number of possible outcomes. It provides an estimate of the probability based on observed data or events.
| Related Links | |
| Coin Toss Probability Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Empirical Probability Formula
What is empirical probability?
How is empirical probability calculated?
When is empirical probability used?
What is the difference between empirical probability and theoretical probability?










