Molecular Speed Formula: The molecular speed of particles in a gas is a measure of how fast those particles are moving on average. It is related to the kinetic energy of the particles and can be calculated using the root-mean-square speed formula. The molecular speed formula is as follows:
-
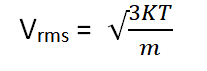
v
rms
is the root-mean-square speed (m/s).
-
k is the Boltzmann constant
(1.380649×10
−23
J/K).
-
T is the absolute temperature in Kelvin (K).
-
m is the mass of one molecule or atom in the gas (kg).
Also Check -
Ammonium Nitrate Formula
Molecular Speed Definition
The root-mean-square speed, v
rms
represents the average speed of gas molecules or atoms in a gas sample at a particular temperature. It is an important concept in kinetic theory and is used to describe the distribution of speeds in a gas. The formula takes into account the temperature and the mass of the particles, showing that at higher temperatures or lower particle masses, the root-mean-square speed will be greater.
Also Check -
Chemistry Formula For Solubility Product
Molecular Speed Applications
Molecular speed, represented by the root-mean-square speed ( v rms ), is a crucial concept in understanding gas behavior and kinetic theory. At its core, it quantifies the average speed of gas particles, impacting various disciplines. Applications encompass gas pressure explanation, indirect temperature determination, influence on chemical reaction rates through collision dynamics, and significance in effusion and diffusion processes.
Molecular speed drives gas separation techniques like gas chromatography and plays a role in the ideal gas law, governing gas behavior. Furthermore, it affects thermal conductivity and aids in modeling celestial bodies in astronomy. it emerges as a fundamental concept underpinning numerous scientific and engineering principles, enriching our understanding of natural phenomena and facilitating technological advancements.
Also Check -
Elevation of Boiling Point Formula
Molecular Speed Formula Solved Examples
1.Helium Gas at Room Temperature: Let's calculate the root-mean-square speed of helium (He) gas molecules at room temperature, which is approximately 298 Kelvin. The molar mass of helium ( He) is approximately 4.0026 g/mol. First, we need to convert the molar mass to kilograms ( kg/mol):
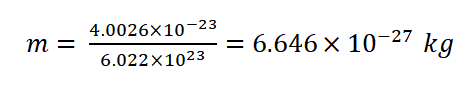
Now, we can calculate v
rms
using the formula:
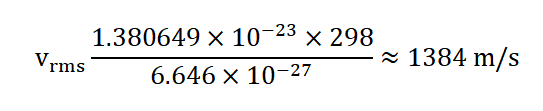
So, at room temperature, the root-mean-square speed of helium gas molecules is approximately 1,384 m/s.
2.Nitrogen Gas at 500 Kelvin: Let's calculate the root-mean-square speed of nitrogen ( N
2
) gas molecules at a temperature of 500 Kelvin. The molar mass of N
2
is approximately 28.0134 g/mol, which is equivalent to about 4.651×10
−26
kg/mol. Using the formula:
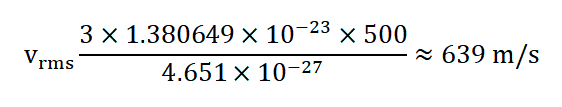
So, at 500 Kelvin, the root-mean-square speed of nitrogen gas molecules is approximately 639 m/s.
3.Carbon Dioxide Gas at 273 Kelvin: Let's calculate the root-mean-square speed of carbon dioxide (CO
2
) gas molecules at the temperature of 273 Kelvin (which is equivalent to 0 degrees Celsius). The molar mass of CO
2
is approximately 44.01 g/mol, or 7.308×10 −
27
kg/mol. Using the formula:
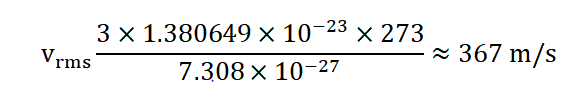
So, at 273 Kelvin (0 degrees Celsius), the root-mean-square speed of carbon dioxide gas molecules is approximately 367 m/s.
4.Hydrogen Gas at 500 Kelvin: Let's calculate the root-mean-square speed of hydrogen ( H
2
) gas molecules at a temperature of 500 Kelvin. The molar mass of H
2
is approximately 2.016 g/mol, which is roughly 3.347×10 −
27
kg/mol. Using the formula:
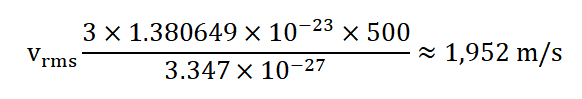
So, at 500 Kelvin, the root-mean-square speed of hydrogen gas molecules is approximately 1,952 m/s.
The root-mean-square speed calculation for diverse gases under varying temperature conditions, considering their distinct molar masses. It's essential to recognize that the root-mean-square speed serves as a valuable metric for assessing the typical velocity of gas particles within a specific thermal environment. This understanding contributes significantly to our comprehension of the dynamic behavior and motion of gas molecules in kinetic theory and has wide applications in fields like chemistry, physics, and engineering.
