NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1: Coordinate Geometry Class 10 Exercise 7.1 is an important part of the CBSE Class 10 Maths syllabus, helping students understand the basics of locating points on the Cartesian plane.
This exercise builds a foundation for advanced concepts by teaching how to plot points using ordered pairs and interpret their positions on the x–y plane.
Practicing Exercise 7.1 improves accuracy, strengthens conceptual clarity, and boosts problem-solving skills—making it highly valuable for scoring well in exams. Regular practice of such exercises not only enhances confidence but also prepares students effectively for higher-level mathematics.
Class 10 Maths Coordinate Geometry Exercise 7.1 With Solutions
Solve the following Questions.
(i) (2, 3), (4,1)
(ii) (–5, 7), (–1, 3)
(iii) (a, b), (–a, –b)
Answer:
(i) Distance between the points is given by
= .png)
= √4+4 = √8 = 2√2(ii)Applying Distance Formula to find distance between points (–5, 7) and (–1, 3),
= 
= √16+16 = √32 = 4√2we get l =
= 
= 
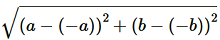2. Find the distance between the points (0, 0) and (36, 15). Also, find the distance between towns A and B if town B is located at 36 km east and15 km north of town A.
Answer:
Applying the Distance Formula to find the distance between points (0, 0) and (36, 15),
= √1296 + 225 = √1521 = 39. Yes, we can find the distance between the given towns A and B.3. Determine if the points (1, 5), (2, 3), and (–2, –11) are collinear.
Answer:
Let A = (1, 5), B = (2, 3) and C = (–2, –11). Using the Distance Formula to find the distance AB, BC, and CA.
Since AB+BC ≠ CA, therefore, the points (1, 5), (2, 3), and (−2, 11) are not collinear.
4. Check whether (5, –2), (6, 4), and (7, –2) are the vertices of an isosceles triangle.
Answer:
Let A = (5, –2), B = (6, 4), and C = (7, –2). Using the Distance Formula to find distances AB, BC, and CA.
Answer:
We have A = (3, 4), B = (6, 7), C = (9, 4) and D = (6, 1) Using Distance Formula to find distances AB, BC, CD and DA, we get
BD = 
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer:
(i) Let A = (–1, –2), B = (1, 0), C= (–1, 2) and D = (–3, 0) Using Distance Formula to find distances AB, BC, CD and DA,
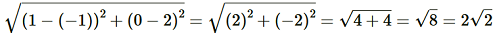
.png)
.png)
(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)
(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2) Using the Distance Formula to find distances AB, BC, CD, and DA,
we get AB =
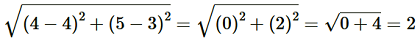
7. Find the point on the x–axis which is equidistant from (2, –5) and (–2, 9).
Answer:
Let the point be (x, 0) on x–axis which is equidistant from (2, –5) and (–2, 9).
⇒ 
8. Find the values of y for which the distance between the points P (2, –3) and Q (10, y) is 10 units.
Answer:
Using the Distance formula,we have
⇒ 
⇒ 64 + (y +3)² = 100 ⇒ (y+3)² = 100-64 = 36 ⇒ y+3 = ± 6 ⇒ y+3=6 or y+3 = - 6Therefore, y = 3 or -9
9. If Q (0, 1) is equidistant from P (5, –3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
Answer:
It is given that Q is equidistant from P and R. Using the Distance Formula,
⇒√25+16 = √x² + 25 ⇒41 = x² + 25 16 = x² x = ± 4. Thus, R is (4, 6) or (–4, 6). 
QR = 
QR = 
10. Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (–3, 4).
Answer:
It is given that (x, y) is equidistant from (3, 6) and (–3, 4). Using Distance formula,
⇒ 
Class 10 Maths Coordinate Geometry Chapter Exercise 7.1
Exercise 7.1 introduces students to the basics of coordinate geometry, including plotting points on the Cartesian plane, understanding coordinates, and interpreting positions accurately.
A detailed PDF with clear, step-by-step solutions is provided to make learning easier and revision faster. This resource is perfect for students preparing Coordinate Geometry Class 10 Exercise 7.1 and aiming to strengthen their fundamentals for exams.
Class 10 Maths Coordinate Geometry Chapter Exercise 7.1
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.1 FAQs
What does Exercise 7.1 of Class 10 Coordinate Geometry cover?
It covers plotting points on the Cartesian plane, distance formula, and midpoint formula.
How does this exercise help in exams?
It builds a strong foundation for coordinate geometry, which is essential for scoring well in Class 10 Maths.
What is the importance of the midpoint formula in coordinate geometry?
The midpoint formula is crucial for finding the center point between two given points, which is often needed in problems related to geometry, symmetry, and constructing shapes.
Are there any tricky questions in this exercise?
The exercise is primarily focused on the application of the distance and midpoint formulas, but some problems may involve multi-step solutions or require careful attention to coordinate signs (positive or negative). However, with practice, these problems become easier to tackle.
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App