
Analysis of Truss: Trusses are widely used in civil and mechanical engineering to construct lightweight and sturdy structures. The analysis of trusses is essential to determine the internal forces in each member, which helps in designing efficient and safe structures. The two main analytical methods for truss analysis are: method of joints and method of section. These methods offer alternative approaches to calculate internal forces in truss members and provide valuable insights into the behavior of complex truss systems.
Assumptions in the Analysis of Plane Truss
The following key assumptions are made for truss analysis:
-
All truss members are idealized as straight elements, and they are connected only at their ends, meaning each member behaves as a straight two-force member.

- All joints are frictionless pin joints.
- Loads (external forces) are only applied at the joints.
- The weight of the members is assumed negligible.
Note:
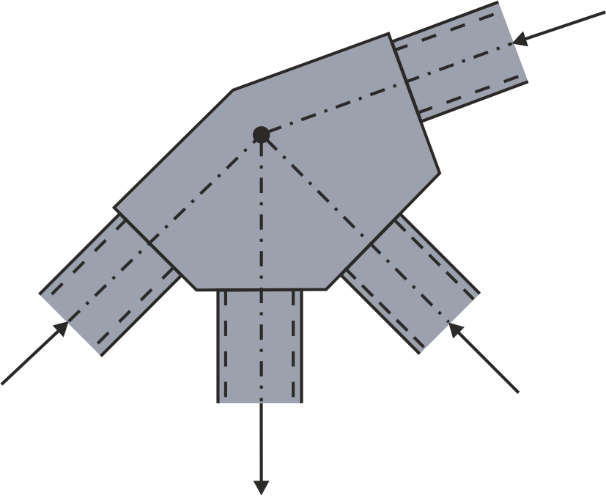
When structural members are connected using welded or riveted joints, it is generally acceptable to assume that the connection acts as a pin joint if the centerlines of the members intersect at the joint, as shown in the figure below:
Methods of Joints
The Method of Joints is a systematic approach used to analyze truss structures by considering equilibrium at each joint or node. The method therefore deals with the equilibrium of concurrent forces, and only two independent equilibrium equations are involved. The subsequent steps outline the Method of Joints for truss analysis.
Step 1:
Calculate support reactions by considering the equilibrium of the entire truss structure, if needed.
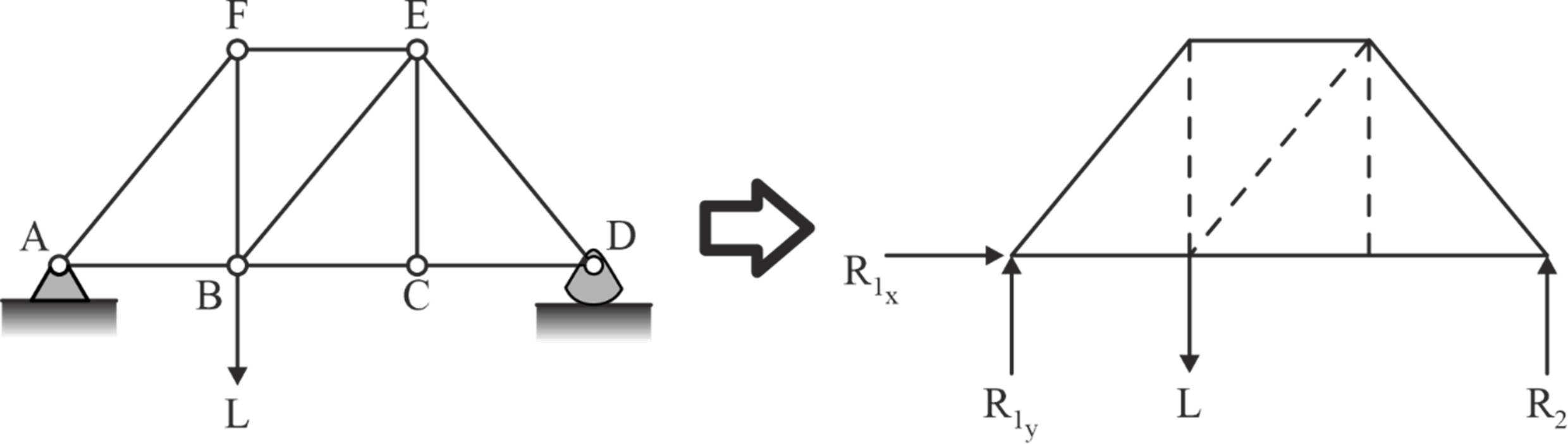
Step 2: Consider the equilibrium of any joint where at least one known load exists and where not more than two unknown forces are present.
Step 3:
Draw the FBD of the joint. (In the FBD, for members with unknown force directions, assume either tension or compression.).
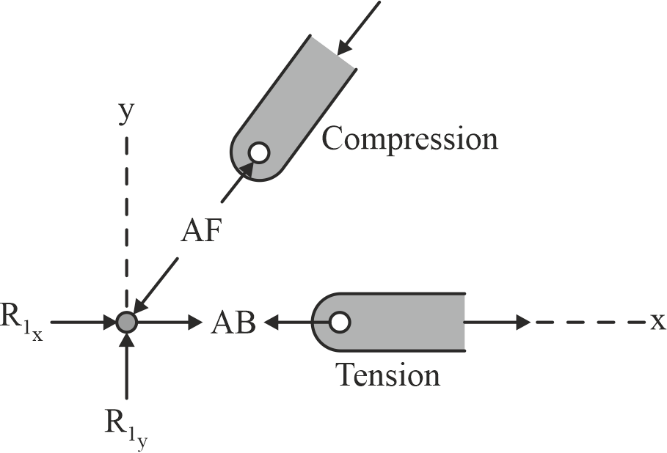
Step 4: Apply the equations of equilibrium ( ∑F x = 0 and ∑F y = 0 ) at the joint to calculate the unknown forces.
Example Problem
Calculation of force in member AB and BC in given plane truss.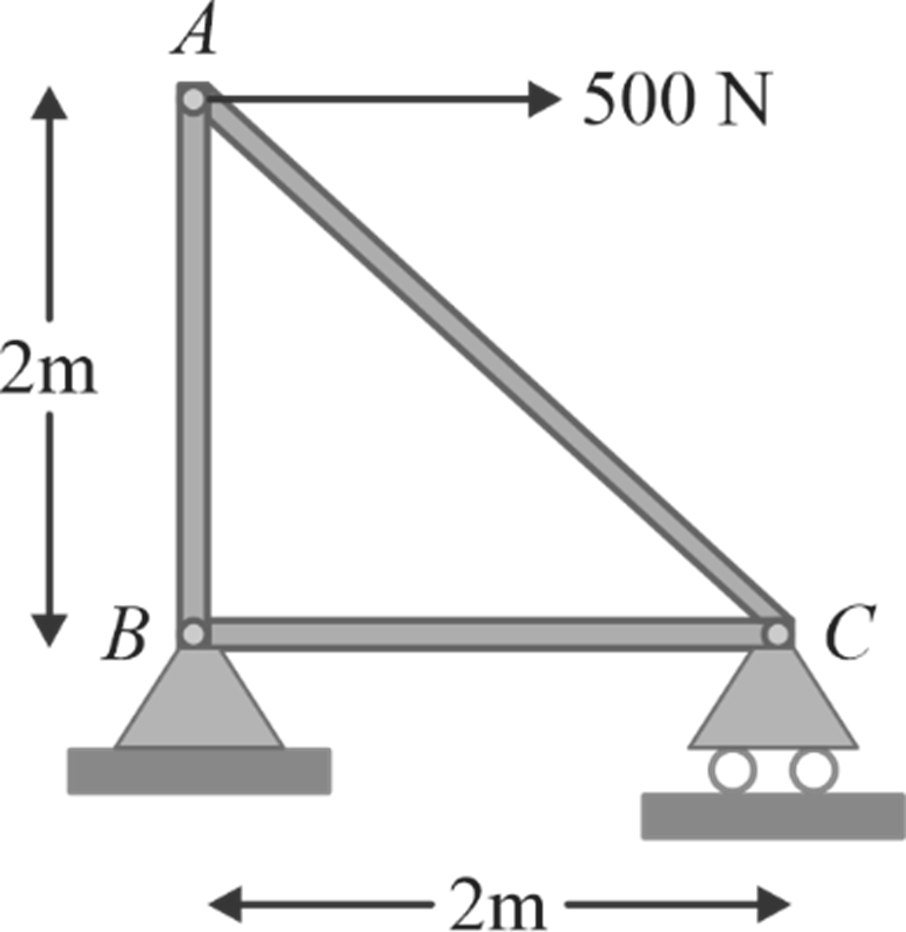 In the given problem, there is no need to calculate the support reactions as we can directly identify a joint where there is one known force and two unknown forces.
In the given problem, there is no need to calculate the support reactions as we can directly identify a joint where there is one known force and two unknown forces.
Consider equilibrium of joint A:
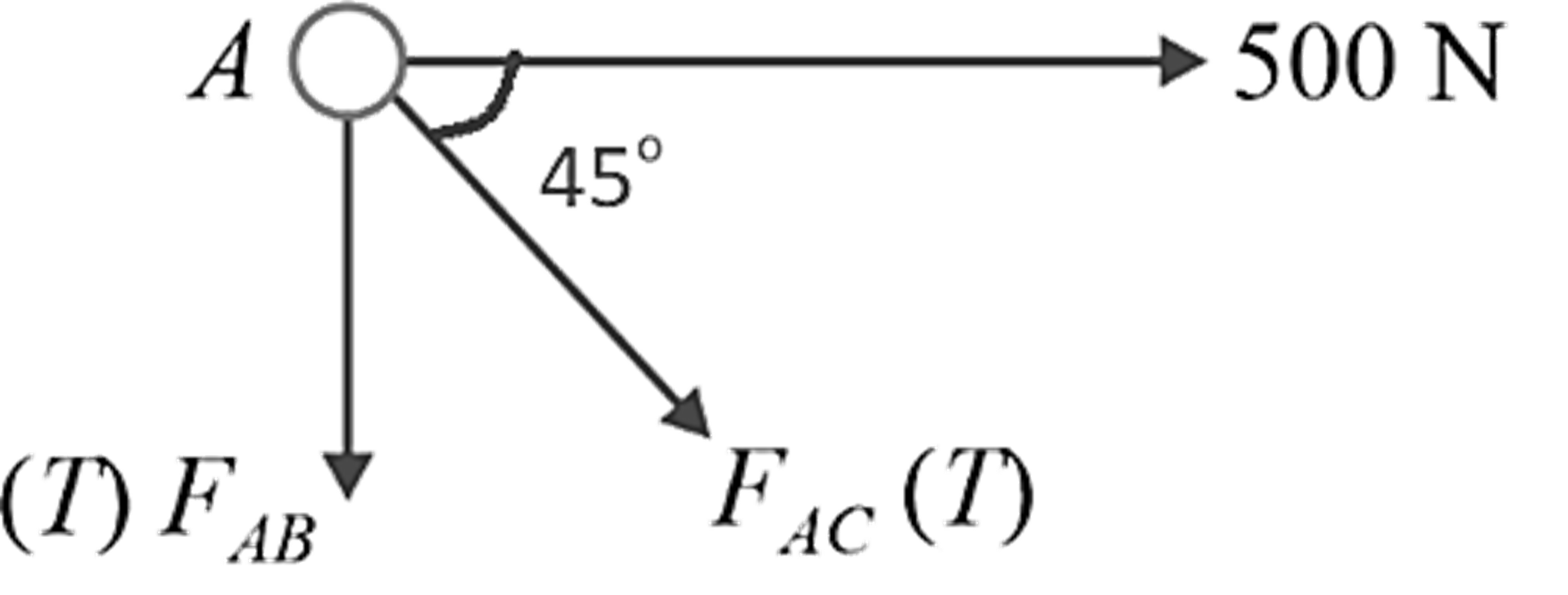
∑F x = 0
F AC cos 45° + 500 = 0
F AC = – 707.1 N = 707.1 N (Compression)
∑F y = 0
F AB – F AC sin 45° = 0
F AB = 500 N = 500 N (Tension)
Consider equilibrium of joint
C:
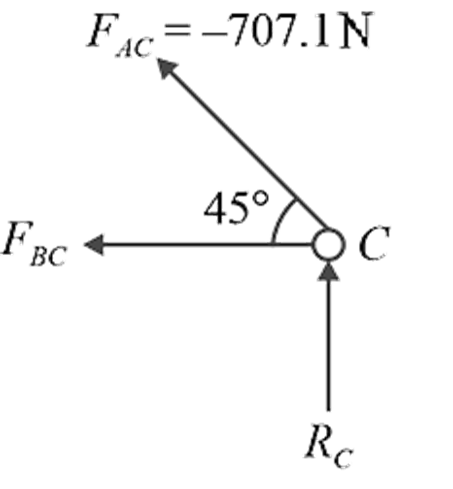
∑F x = 0
F BC – 707.1 cos 45° = 0
F BC = 500 N (Tension)










