

General Plane Motion
Motion is a fundamental concept in engineering mechanics, and understanding the kinematics of motion is crucial for analyzing and solving engineering problems. General plane motion is the most common form of general motion encountered in engineering applications. General plane motion refers to the complex movement of an object in which it simultaneously undergoes translation and rotation.
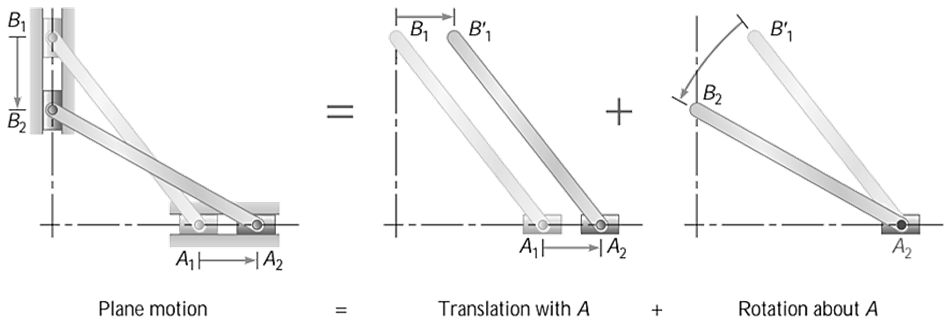
However, this complex general motion of the ladder can be studied by breaking it into two parts (i) a translation from A 1 B 1 to A 2 B’ 1 as shown in above figure, and (ii) a counterclockwise rotation by an angle θ about an axis perpendicular to the plane and passing through its end A 2 from the position A 2 B’ 1 to A 2 B 2 as shown in above figure.
Methods of Motion Analysis in General Motion
To describe and analyse general motion, we need to use a combination of formulas that deal with translational, and rotational motion. We mostly used two methods for the kinematic analysis of general plane motion.

Relative Velocity Method
The relative velocity method simplifies the complex analysis of general plane motion. To apply this method effectively, you should start by understanding the problem thoroughly and selecting an appropriate reference frame. Break down the motion into translational and rotational components. Then, calculate the relative velocity using specific equations for translational and rotational motion. Combine these relative velocities to understand the overall motion of the system.
-
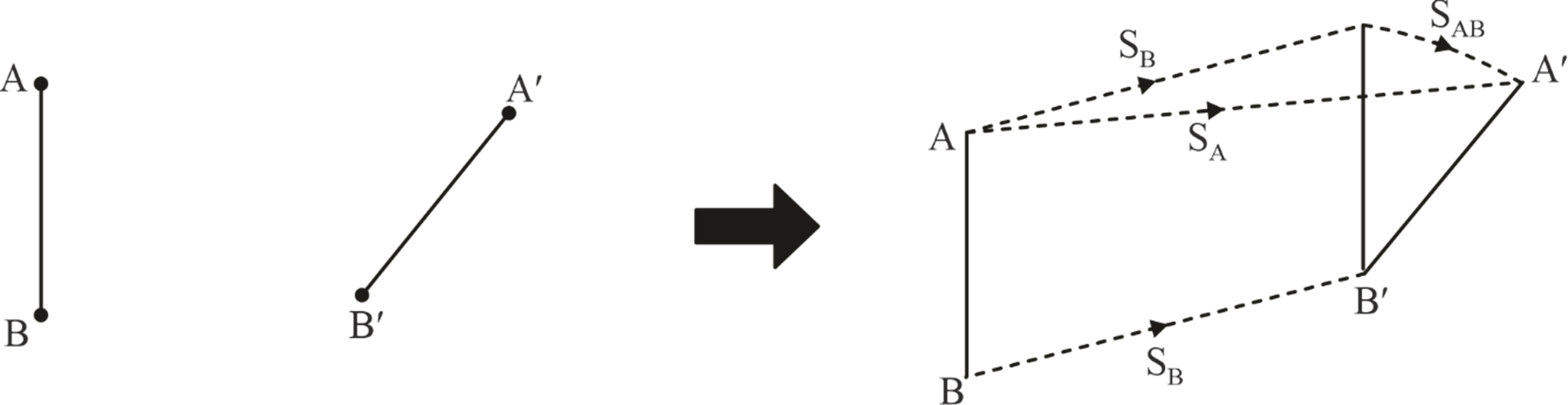
When point B is taken as the reference, the displacement of end A is the vector sum of the displacement of end B (resulting from translation) and the displacement of end A relative to end B (caused by rotation).
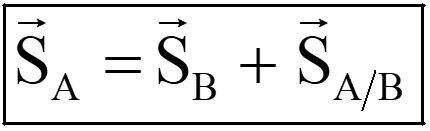
-
With B chosen as the reference point, the velocity of end A;
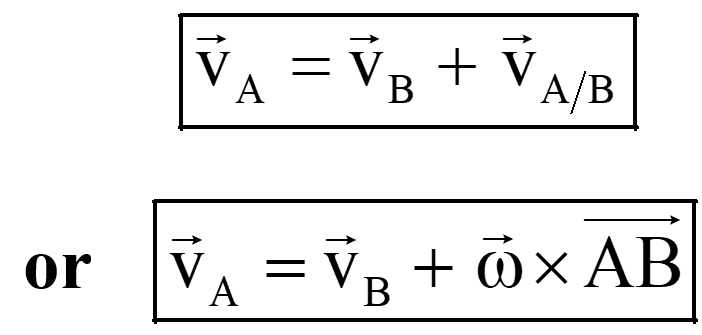
Where,
![]() denotes the velocity of point A relative to point B, and its orientation is perpendicular to the line AB.
denotes the velocity of point A relative to point B, and its orientation is perpendicular to the line AB.
Note: The component of relative velocity between any two points on a rigid body along the axis connecting those two points is equal to zero.
-
With B chosen as the reference point, the acceleration of end A;
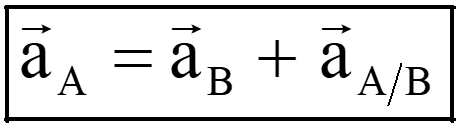
Where,
![]() denotes the acceleration of point A relative to point B.
denotes the acceleration of point A relative to point B.
![]()
Instantaneous Center Method
The combined motion of rotation and translation may be assumed to be a motion of pure rotation about some imaginary point known as the instantaneous center of rotation or instantaneous center of velocity . As the position of body goes on changing, therefore the instantaneous center also goes on changing.
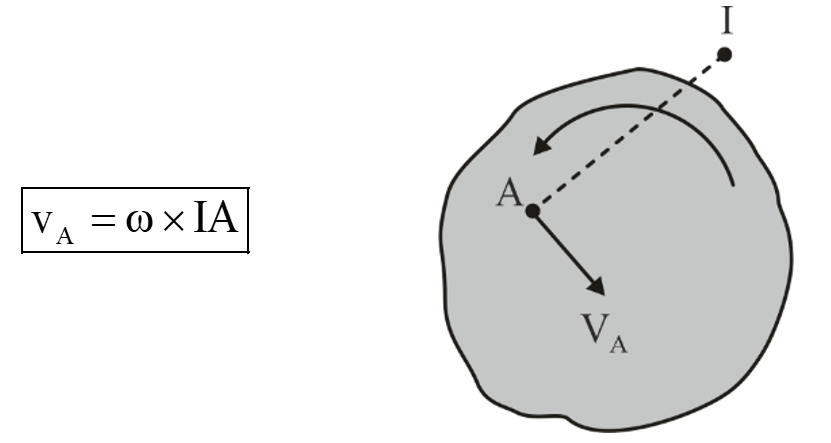
It simplifies complex motion analysis problems by reducing them to rotational motion around the instantaneous center. This analysis can be broken down into two main steps: first, determining the position of the instantaneous center, and second, utilizing equations to examine the rotational motion around this IC point.
Location of Instantaneous Center
Case 1:
When the direction of velocities of two particles A and B are known, and V
A
is not parallel to V
B
.
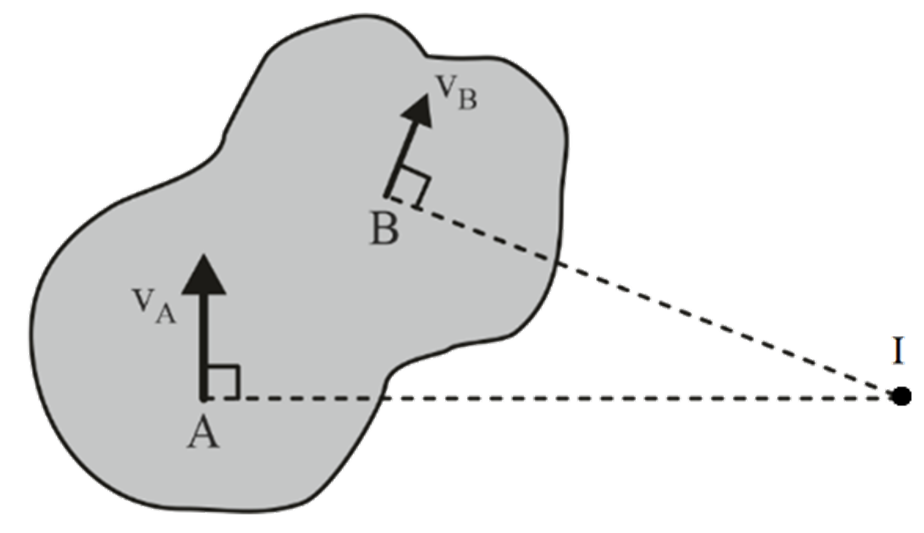
I center lies at the intersection of two lines drawn at A and B, perpendicular to V A and V B
Case 2:
When the direction and magnitude of the velocities of two particles A and B are known, and V
A
is parallel to V
B
.
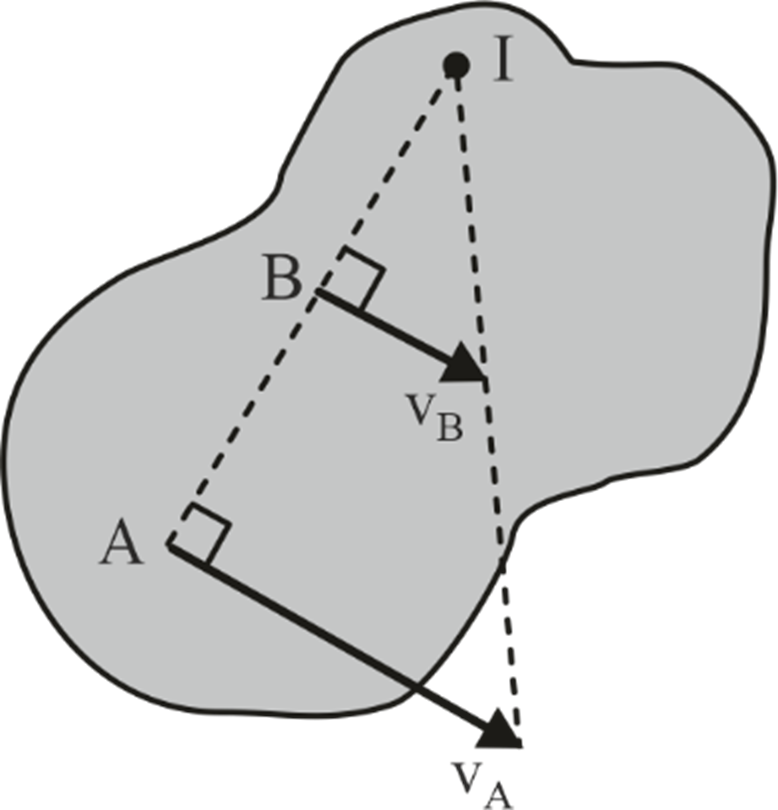
The I center lies at the intersection of two lines, one joining the extremities of vectors V A and V B and the other joining points A and B.
Case 3:
Object rolling without slipping on a fixed surface.
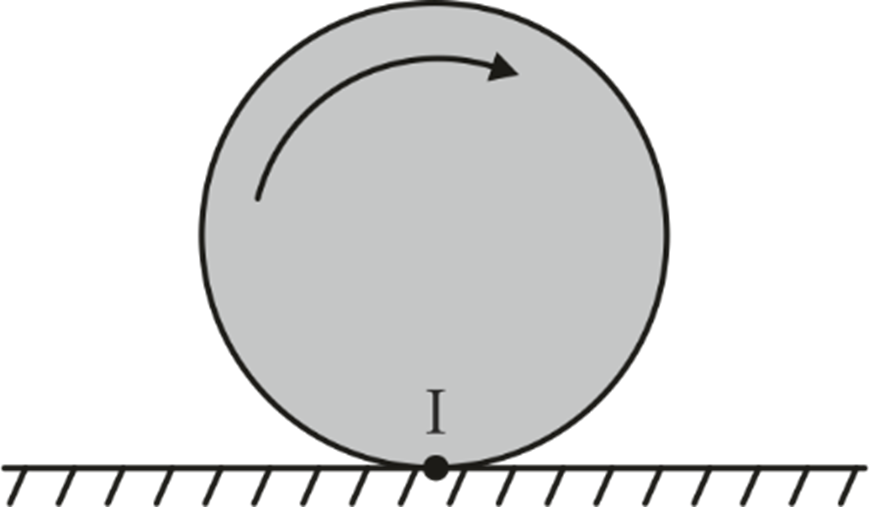
I center lie at the point of contact at that instant.











