Impulse Momentum Method

Impulse Momentum Method: In engineering, some problems involve understanding what makes objects move and how they move. This falls under the branch of dynamics known as "kinetics." Kinetics is a branch of mechanics that deals with the study of forces and their effects on the motion of particles and rigid bodies. In engineering mechanics, understanding the kinetics of particles and rigid bodies is fundamental to solving practical engineering problems.

The impulse momentum method is a fundamental concept in engineering mechanics that allows us to analyze the motion of particles and rigid bodies by considering the change in momentum they experience due to external forces and impulses.

Impulse of Force

Impulse is the product of a force acting on an object and the time duration for which the force is applied. Mathematically, it is expressed as:

Where, I is the linear impulse, F(t) is the force as a function of time, and t ₁ and t ₂ are the initial and final times, respectively. From the above equation, it can also be concluded that the area under the force-time (F−t) curve between two instant t ₁ and t ₂ represents the impulse of a force acting on an object.

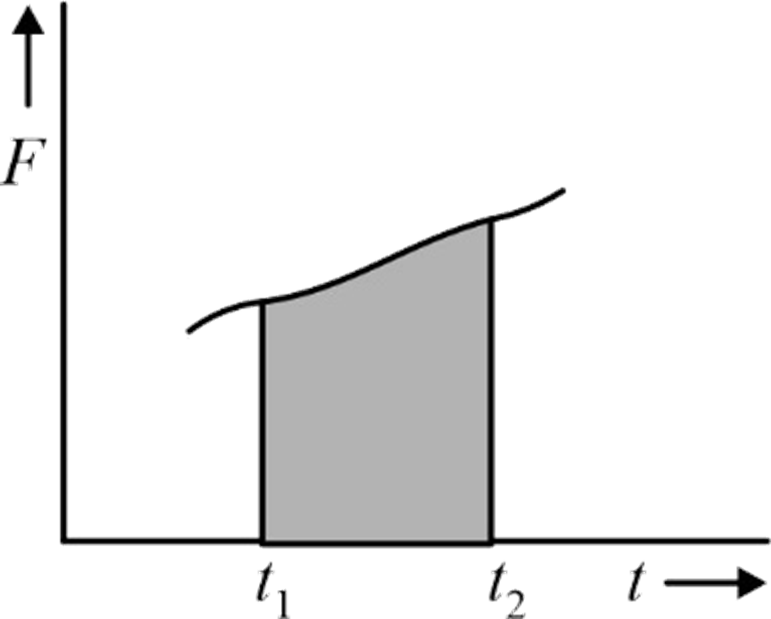
Note: Impulse of a torque or angular impulse is given as:

Momentum

Linear momentum, or simply momentum, is defined as the product of an object's mass (m) and its velocity (v) and is a vector quantity. Mathematically, momentum (p) is expressed as:

Note: Angular momentum (L) is defined as the cross product of the object's moment of inertia (I) and its angular velocity (ω). The formula for angular momentum is as follows:

Linear Impulse Momentum Method

This method is especially valuable when dealing with time-varying forces and can provide deep insights into the behavior of objects in motion. The linear impulse-momentum equation establishes a quantitative relationship between the impulse of force and the change in momentum experienced by the object. Integration of Newton’s 2nd law over the time interval from t ₁ to t ₂ results in impulse momentum relation. Mathematically, it can be expressed as follows:

Linear Impulse = Final linear momentum – Initial linear momentum

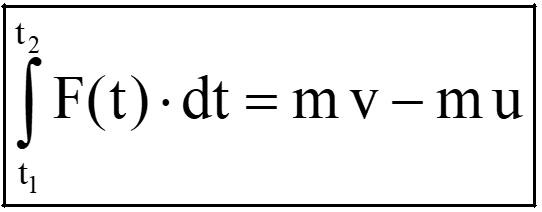
Note: if the net force is the constant (i.e., not the function of time), then

Angular Impulse Momentum Method

This method is especially valuable when dealing with time-varying forces torque and can provide deep insights into the behavior of objects in motion. The angular impulse-momentum equation establishes a quantitative relationship between the angular impulse and the change in angular momentum experienced by the object. Mathematically, it can be expressed as follows:

Angular Impulse = Final angular momentum – Initial angular momentum

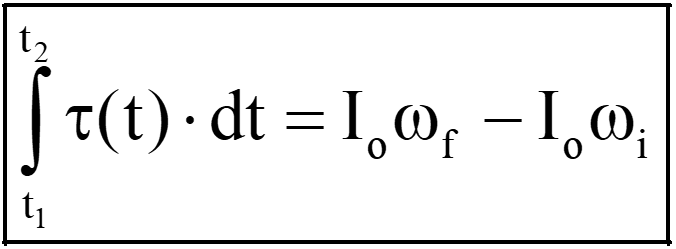
Note: if the net torque is the constant (i.e., not the function of time), then

Analysis using Impulse Momentum Relation

When a rigid body engages in motion, whether it's translation, rotation, or a combination of both, its dynamic behaviour can be evaluated by equations.

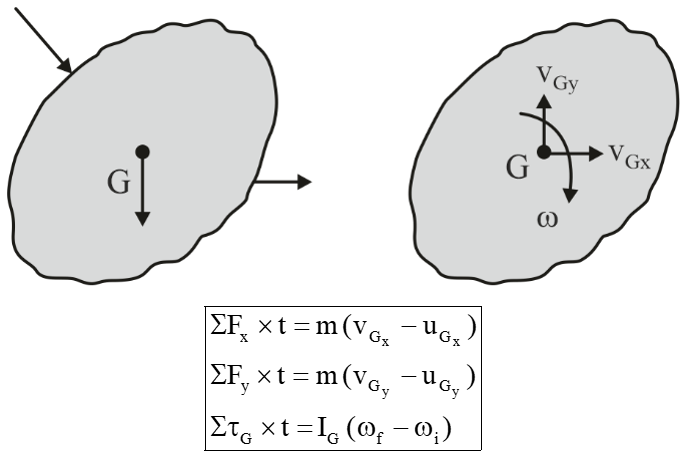
Conservation of Momentum

When the resultant of the external forces acting on a system of particles is zero, the linear momentum of the system is conserved.

Impulse of a force = Final momentum – Initial momentum

Conservation of Angular Momentum

When the net moment acting on a rigid body is zero, the angular momentum of the system is conserved.

Initial angular momentum = Final Angular Momentum