Lagrange's Equation, Check Steps for Analysis

Lagrange's Equation: Mechanics, a fundamental branch of engineering, offers various approaches to solving complex problems related to motion and forces acting upon physical bodies. The most common approaches to solving the problem of mechanics are shown below.

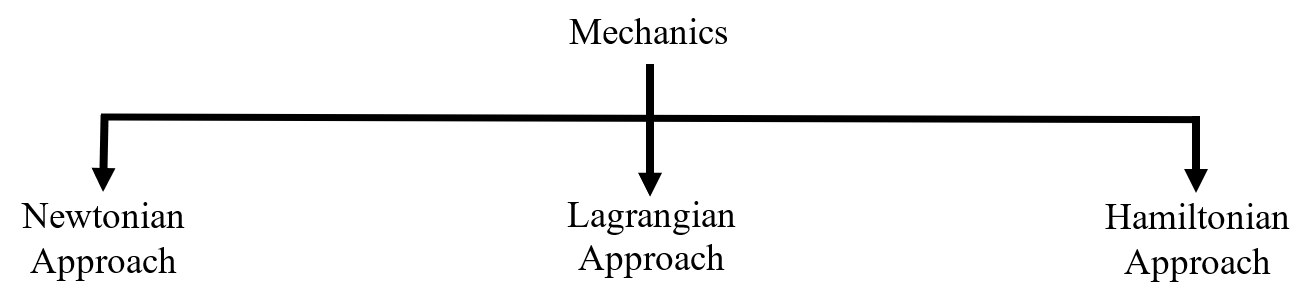
In the field of mechanics, the choice of approach depends on the specific problem at hand. While the Newtonian approach serves as a fundamental and intuitive framework for most engineering applications, the Lagrangian and Hamiltonian approaches offer powerful tools for tackling complex and constrained systems.

Lagrange's Equation

The Lagrangian mechanics, formulated by Joseph-Louis Lagrange, is a powerful mathematical approach that describes the motion of particles and systems using a quantity known as the Lagrangian. The central idea behind this approach is to formulate the equations of motion by considering the difference between the kinetic and potential energies of a system, without the need for force-based equations.

It introduces generalized coordinates and derives equations of motion based on the minimization of a quantity. It simplifies complex systems by reducing the number of equations of motion, making it a valuable tool for advanced engineering applications.

• Lagrange's Equations are a set of second-order differential equations derived from the principle of least action.
• Lagrange's Equation describe the motion of a mechanical system by utilizing a set of generalized coordinates and their corresponding generalized forces, which are related to the potential and kinetic energies of the system.
• The general form of Lagrange's equations is given by:

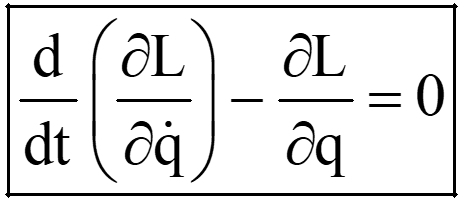
Where L represents the Lagrangian (i.e, Lagrange’s function) of the system and q represents the generalised coordinates. Solving these equations provides a complete description of the system's behavior.

Lagrange’s Function

The Lagrange’s Function of the system is the the difference between the system's kinetic energy (T) and potential energy (U).

Where L is Lagrange's function, T represents the kinetic energy of the system, and U represents the potential energy of the system. Here, kinetic and potential energy equations must be in terms of generalised coordinate. The generalised coordinates are the minimum number of independent coordinates required to define the system. The generalised coordinates are used to derive the equations of motion for the system, which determine how the coordinates change as functions of time.

Steps for Analysis using Lagrange’s Equation

To apply the Lagrangian approach to solve problems in mechanics, one must follow these essential steps:

• Selection of Generalized Coordinates: Begin by identifying a set of generalized coordinates (q ₁ , q ₂ , q ₃ , …. q _n ) that describe the configuration of the system. Generalized coordinates are independent variables that uniquely specify the position of all particles in the system.
• Formulation of Kinetic and Potential Energies: Calculate the kinetic energy (T) and potential energy (U) of the system in terms of the chosen generalized coordinates. Kinetic energy is related to the velocities of the system components, while potential energy depends on positions and forces. Express both T and U as functions of the generalized coordinates and their time derivatives.
• Formulation of Lagrange’s Function : Combine the expressions for T and U to construct the Lagrange’s function (L = T − U) for the system.
• Derive Equation of Motion: To obtain the equations of motion for the system evaluate partial derivatives and for each generalized coordinate, apply the Euler-Lagrange equation for each generalized coordinate q _i .
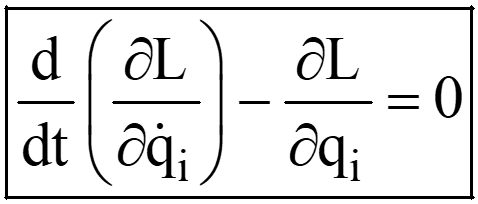
• Solve the Equation of Motion. Solve the obtained differential equations to determine the time evolution of the generalized coordinates. The solutions provide information about the system's motion, including positions, velocities, and accelerations as functions of time.

Lagrange's Function for Some Example Problems

Problem	Kinetic Energy	Potential Energy	Lagrange’s Function
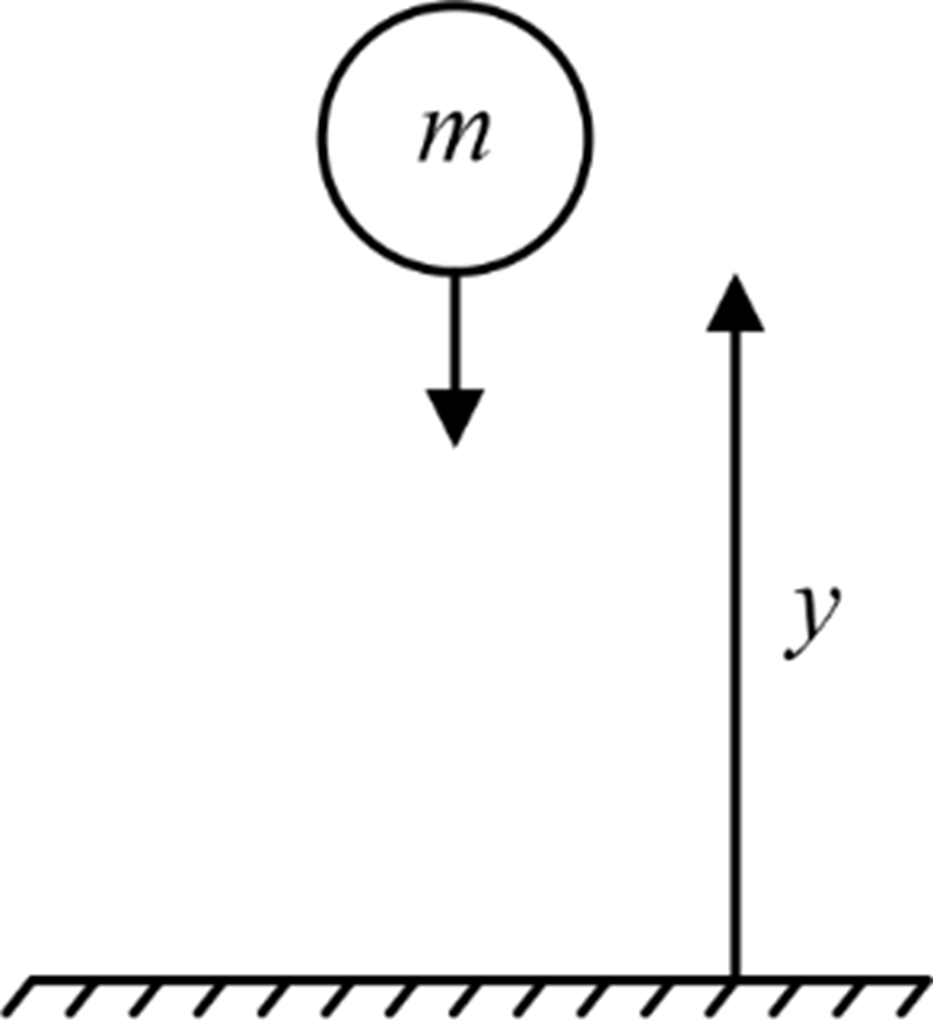
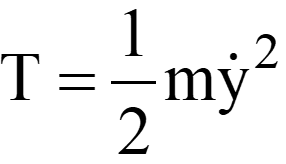
	(In this problem, y is the generalized coordinate)	U = m g y
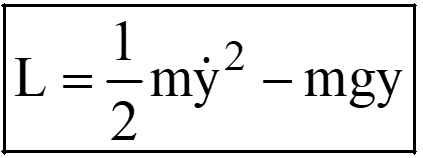
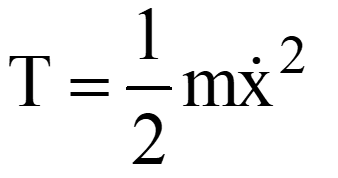
	(In this problem, x is the generalized coordinate)
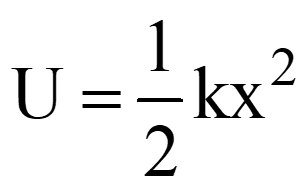
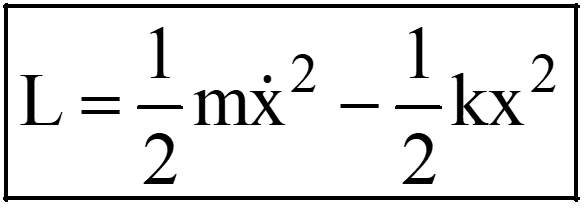