Resultant Force
When an object is subjected to a single force, predicting its motion becomes relatively straightforward. However, the complexity arises when the object experiences a system of forces acting upon it simultaneously. In such cases, accurately determining the resultant force becomes essential to predict the object's motion and establish its equilibrium.
The resultant force, also known as the net force, is the single force that represents the combined effect of multiple forces acting on an object.
This resultant force possesses the same effect on the object as the combined effect of all the individual forces. It provides a concise description of the overall influence exerted on the object, considering both the magnitudes and directions of the individual force.
Composition of Forces
The term "composition of forces" refers to the process of determining the resultant force of multiple forces acting on an object. To calculate the resultant force, we must consider both the magnitude and direction of each individual force acting on an object. By employing vector analysis techniques, we can determine the resultant force using two common methods: the graphical method and the analytical method.
Resultant of a Concurrent Force System : Two Forces
To find the resultant of two forces, we can utilize either the parallelogram law or triangle law.
Parallelogram Law
“If two forces acting a point, are represented in magnitude and direction by the two adjacent sides of a parallelogram, their resultant is represented in magnitude and direction by the diagonal of the parallelogram drawn from the same point.”
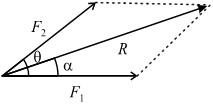
Magnitude of resultant force is given by the relation;
Where F
1
and F
2
are the component forces, and θ is the angle between the forces F
1
and F
2
.
Direction of resultant force with the force F
1
is given by the relation;
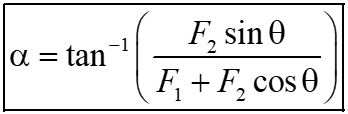
The parallelogram law, being an analytical method, is often favored over the graphical method for its ability to provide accurate results through straightforward calculations.
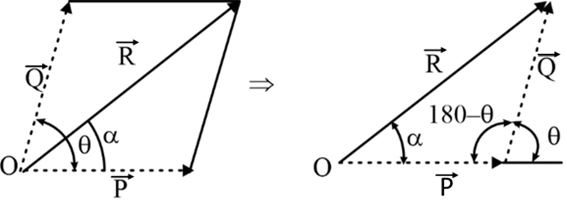
Triangle Law
“When two forces acting at a point can be represented by two adjacent sides of a triangle in a specific order, the third side of the triangle taken in the opposite order represents the resultant force, indicating both its magnitude and direction”. The Triangle law, which is a graphical method, is a corollary of the Parallelogram law.
Resultant of a Concurrent Force System : More than Two Forces
When seeking to find the resultant of multiple forces, two commonly used methods are the method of projections (resolutions) and the polygon Law.
Method of Resolution
Resolution of forces involves breaking down a single force into multiple components that collectively produce the same effect on an object as the original force would have. The step-by-step process for calculating the resultant force using the method of resolution is outlined below:
-
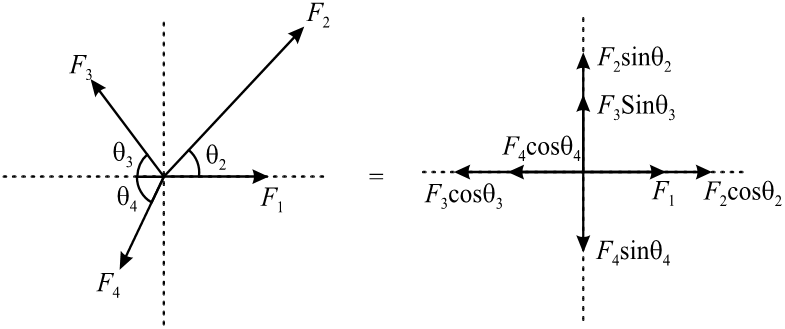
Step 1:
Calculate the horizontal and vertical components of each force.
-
Step 2:
Sum up all the horizontal components to find the total horizontal component of the resultant force, considering proper sign convention.
-
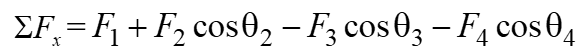
Step 3:
Sum up all the vertical components to find the total vertical component of the resultant force, considering proper sign convention.
-
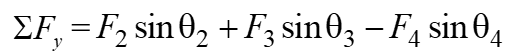
Step 4:
Use these total components to calculate the magnitude and direction of the resultant force using the Pythagorean theorem and trigonometric functions.
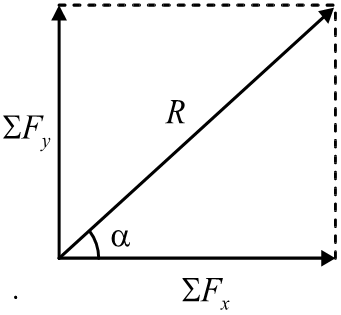Resultant force and its direction can be calculated by using the relation;
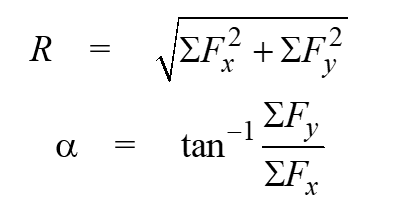
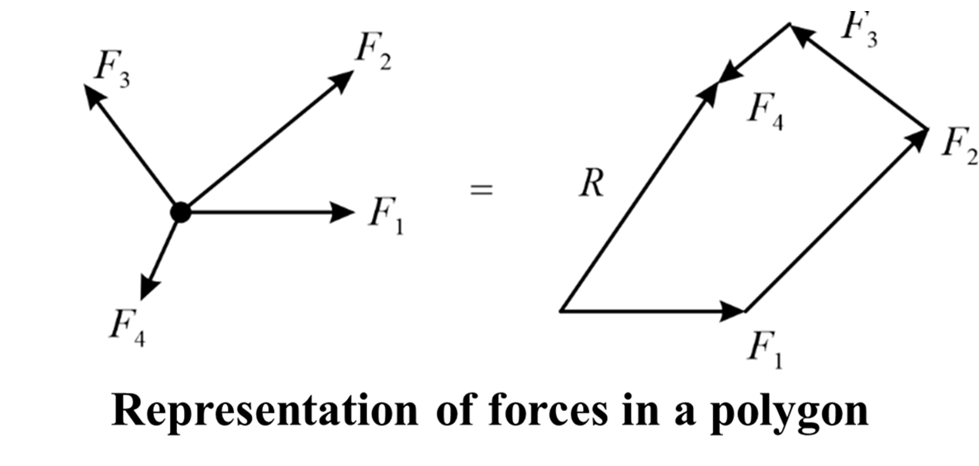
Polygon Law
The Polygon Law of force addition states that when multiple forces are represented by the sides of a polygon, taken in the same order, the resultant force can be represented by the closing side of the polygon, taken in the opposite order, in terms of magnitude and direction.
Resultant of a Parallel Force System
The step-by-step process for calculating the resultant force of parallel force system is outlined below:
-
Step 1:
Do the algebraic sum of all parallel forces to find the resultant force, considering proper sign convention.
R = F
1
+ F
2
– F
3
-
Step 2:
Take the algebraic sum of the moment of all forces about any reference point (say A), considering proper sign convention.
-
Step 3:
Use Varignon’s theorem to calculate the position of resultant force R from point A.
Resultant of a Non-Concurrent Non-Parallel Force System
The step-by-step process for calculating the resultant force of non-concurrent non-parallel force system is outlined below:
-
Step 1:
Calculate the horizontal and vertical components of each force.
-
Step 2:
Sum up all the horizontal components to find the total horizontal component of the resultant force, considering proper sign convention.
-
Step 3:
Sum up all the vertical components to find the total vertical component of the resultant force, considering proper sign convention.
-
Step 4:
Use these total components to calculate the magnitude and direction of the resultant force using the Pythagorean theorem and trigonometric functions.
Resultant force and its direction can be calculated by using the relation;
-
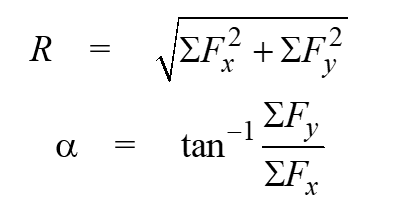
Step 5:
Take the algebraic sum of the moment of all forces about any reference point (say O), considering proper sign convention.
-
Step 6:
Use Varignon’s theorem to calculate the position of resultant force R from point O.
Varignon's Theorem
Moment of a force about any point is equal to the sum of the moments of the components of that force about the same point. This method is employed to determine the position of the resultant force in a system of parallel or non-concurrent non-parallel forces.
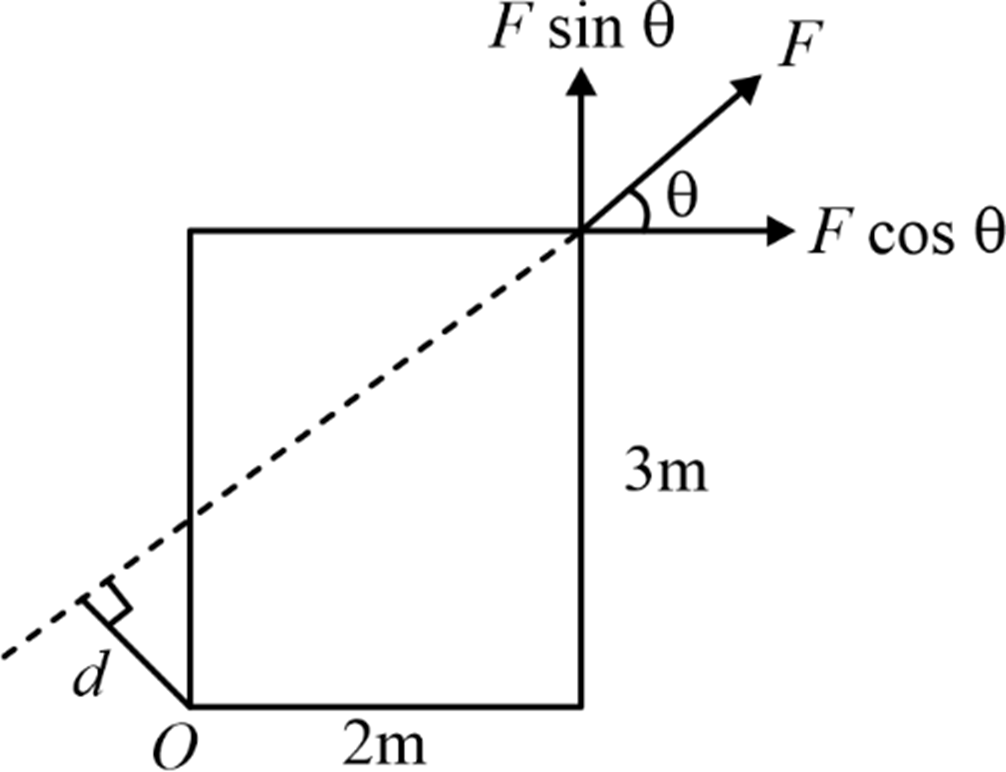
Moment of force F about point O:
M
O
= F × d = (F cos θ
) × 3 – (F sin θ
) × 2
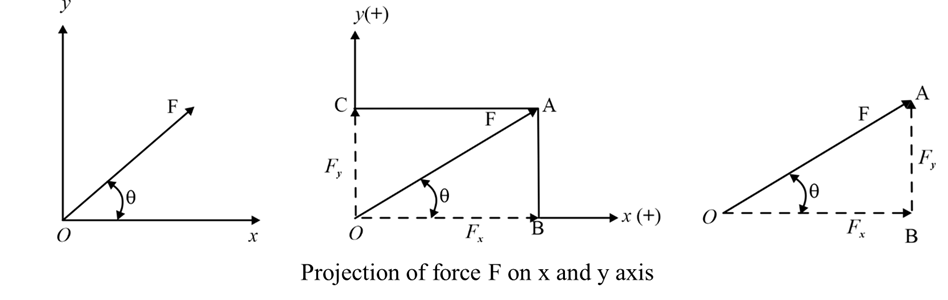
Resolution of a Force F into Rectangular Components
The rectangular components of a force refer to the two perpendicular components of that force that act along two specific axes, typically the x-axis and y-axis in a Cartesian coordinate system. These components make it easier to analyze the effect of the force in different directions
.
By trigonometry, we have the relation of component forces F
x
and F
y
with force F and θ;
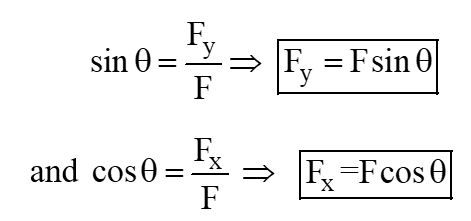
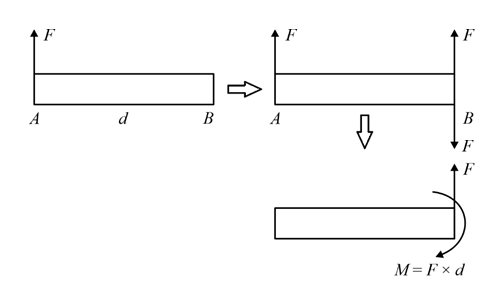
Shifting of a Force to a Parallel Position
The parallel shift of force F from point A to point B can be accomplished by combining force F with a couple (i.e., F×d). where d is the perpendicular distance between two parallel position.
