Degree of Freedom (f) :
We will start with the fact that degree of freedom is
The minimum number of ways in which motion of a body (or a system) can be described completely is called its degree of freedom. Degrees of freedom (
f
) is defined as the total number of possible independent significant ways in which a system can have energy. The independent motions can be translational, rotational or vibrational or any combination of them.
A particle moving in a straight line can have only one degree of freedom. i.e., translational degree of freedom. Similarly, a particle moving in a plane have two translational degrees of freedom and a particle free to move in space have three translational degrees of freedom. This discussion is followed by degree of freedom of solid, non-linear polyatomic gas and diatomic gases.
Degree of Freedom (f)
The minimum number of ways in which motion of a body (or a system) can be described completely.
is called its degree of freedom.
Degree of Freedom Examples
In Fig, block has one degree of freedom, because it is confined to move in a
straight line and has only one translational degree of freedom.
In Fig. (b), the particle has two degrees of freedom because it is confined to move in a plane and so it has two translational degrees of freedom. In Fig. (c), the sphere has two degrees of freedom one rotational and another translational. Similarly, a particle free to move in space will have three translational degrees of freedom.
Degree of Freedom of Gas Molecules
A gas molecule can have, the following types of energies
(i)
translational kinetic energy
(ii)
rotational kinetic energy
(iii)
vibrational energy (potential + kinetic)
Vibrational Energy
The forces between different atoms of a gas molecule (interatomic force) may be visualized by imagining every atom as being connected to its neighbours by springs. Each atom can vibrate along the line joining the atoms. Energy associated with this is called vibrational energy.
Degree of Freedom of Monoatomic Gas
A monoatomic gas molecule (like He) consists of a single atom. It can have translational motion in any direction in space. Thus, it has 3 translational degrees of freedom.
f
= 3 (all translational). It can also rotate but due to its small moment of inertia, rotational kinetic energy is neglected.
Degree of Freedom of a Diatomic and Linear Polyatomic Gas
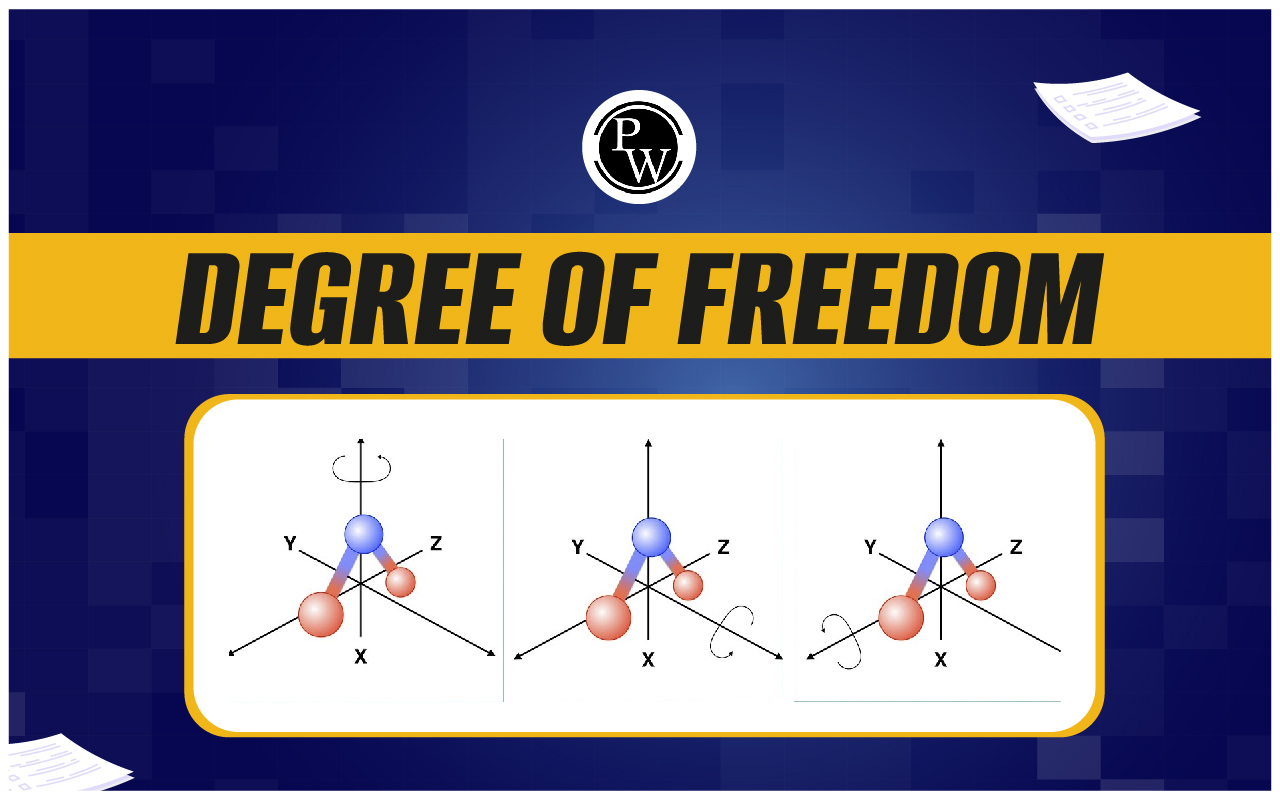
The molecules of a diatomic and linear polyatomic gas (like O
2
, CO
2
and H
2
) cannot only move bodily but also rotate about anyone of the three coordinate axes as shown in figure. However, its moment of inertia about the axis joining the two atoms (
x
-axis) is negligible. Hence, it can have only two rotational degrees of freedom.
Thus, a diatomic molecule has 5 degrees of freedom: 3 translational and 2 rotational. At sufficiently high temperatures, it has vibrational energy as well providing two more degrees of freedom (one vibrational kinetic energy and another vibrational potential energy). Thus, at high temperatures a diatomic molecule has 7 degrees of freedom, 3 translational, 2 rotational and 2 vibrational. Thus,
f = 5 (3 translational + 2 rotational) at room temperatures and
f = 7 (3 translational + 2 rotational + 2 vibrational) at high temperatures.
Degree of Freedom of Non-linear Polyatomic Gas
A non-linear polyatomic molecule (such as NH
3
) can rotate about any of three coordinate axes. Hence, it has 6 degrees of freedom 3 translational and 3 rotational. At room temperatures, a polyatomic gas molecule has insignificant vibrational energy. But at high enough temperatures it is also significant. So, it has 8 degrees of freedom 3 rotational, 3 translational and 2 vibrational. Thus,
f = 6 (3 translational + 3 rotational) at room temperatures and
f = 8 (3 translational + 3 rotational + 2 vibrational) at high temperatures.
Degree of Freedom of a Solid
An atom in a solid has no degrees of freedom for translational and rotational motion. At high
temperatures, due to vibration along 3 axes it has 6 degrees of freedom.
f = 6 (all vibrational) at high temperatures
Degrees of freedom (f) is defined as the total number of possible independent significant ways in which a system can have energy. The independent motions can be translational, rotational or vibrational or any combination of them. A particle moving in a straight line can have only one degree of freedom. i.e., translational degree of freedom. Similarly, a particle moving in a plane have two translational degrees of freedom and a particle free to move in space have three translational degrees of freedom.
Monatomic gas molecules can be considered as point masses moving in space and they will have only three translational degrees of freedom. However, this does not hold good with polyatomic gases. In a polyatomic molecule we have to take rotational motion of atoms about their centre of mass and the vibrational motion of the atoms relative to each other. Thus, we must write the molecular kinetic energy as.
As the temperature of a gas increases, the different components of the molecular energy also increase. But each component increases in a different manner. Vibrational energy depends on the strength of the bonding of the atoms in the molecule. The stronger the ionic bonds, the more difficult it is to increase the vibrational energy.
On the other hand, the rotational energy depends on the geometry (moment of inertia) of the molecule. But since vibrational energy comes into picture only at high temperatures, vibrational degrees of freedom are not taken into account unless stated in the question. (a) A Monatomic gas has 3 degrees of freedom (all translational). Although a monatomic molecules can also rotate but due to its small moment of inertia rotational kinetic energy is insignificant. (b) A diatomic gas such as H
2
, O
2
etc. are made up of two atoms joined rigidly to one another through a bond. This cannot only move bodily, but also rotate about any one of the three co-ordinate axes.
However, its moment of inertia about the axis joining two atoms is negligible. Hence it can have 3 rotational motions out of which only two rotational motions are significant. Thus, a diatomic molecule has five degrees of freedom, three translational and two rotational. (c) A nonlinear polyatomic gas molecule such as H
2
O, NH
3
etc. can rotate about any of three co-ordinate axes. Hence it has six degrees of freedom, three translational and three rotational. However, a linear polyatomic gas molecule like CO
2
has five degrees of freedom three translational and two rotational (like a diatomic molecule). For a molecule with n atoms there will be 3n degrees of freedom. These can be attributed as follows:
|
Type
|
Translation
|
Rotation
|
Vibration
|
|
Linear
|
3
|
2
|
3
n
– 5
|
|
Non-linear
|
3
|
3
|
3
n
– 6
|
There is no general way in which one can find the degrees of freedom. However, if a system has A number of independent particles and R is the number of independent restrictions between them then the number of degrees of freedom (f) is f = 3A–R (a) For a monatomic gas molecule A = 1 and R = 0 Hence for monatomic gas molecule f = 3. (b) For di-atomic gas molecule At normal temperature A = 2 and R = 1 (as the bond existing between its atoms must be rigid). So, for diatomic gas molecule f = 5.
