Schrodinger Wave Equation, Electron-Density Distribution, Important Topics For JEE 2025
Shrivastav 14 May, 2024
Share
Schrodinger wave Equation : The Schrodinger wave equation is a fundamental equation in quantum chemistry that describes the behavior of a quantum mechanical system, such as an atom or a molecule. It mathematically represents how the wave function of the system evolves over time, providing information about the probability distribution of finding particles, like electrons, within the system. The equation is derived from the principles of quantum mechanics and is used to calculate various properties of atoms and molecules, including energy levels, electron densities, and molecular structures, forming the basis of modern quantum chemistry.
Schrodinger wave Equation : In this article, we'll embark on a journey to demystify Schrodinger's wave equation and explore its solution. By the end of our adventure, you'll have a clearer understanding of this fundamental equation and its significance in describing the behaviour of particles on the atomic and subatomic scales. So, fasten your seatbelts and get ready to dive into the fascinating world of quantum mechanics.
Before we delve into the solution of Schrödinger's wave equation, let's first grasp the essence of this foundational equation in quantum mechanics. Proposed by the Austrian physicist Erwin Schrödinger in 1926, the Schrödinger wave equation is a mathematical equation that describes how the wavefunction of a physical system evolves over time.
Schrodinger wave Equation : The Schrodinger wave equation is solved using mathematical techniques like separation of variables or numerical methods. Solutions yield wave functions, which describe the behavior of quantum systems. These solutions provide information on particle properties, such as energy levels and spatial distributions, crucial in understanding atomic and molecular behavior.
Angular function depends on l and m.
Radical Part of Solution
In the solution of the Schrödinger wave equation, the radical part represents the spatial distribution of the wave function. It describes the probability amplitude of finding a particle, such as an electron, at different locations within the quantum system.
1s
Where
2s
2p
3s
3p
3d
General form :
Graph of Radial Function
Graph of radial function : The graph of the radial function in the Schrödinger wave equation typically depicts the radial probability density distribution of finding an electron at a certain distance from the nucleus in an atom. It often exhibits peaks and troughs, indicating regions of higher and lower electron probability density, respectively, as the distance from the nucleus varies. This graph is essential in visualizing electron behavior and understanding atomic structure.
Graph of radial function [R(r) or ψ (r)] :
Only the graph of s-orbital does not start from origin.
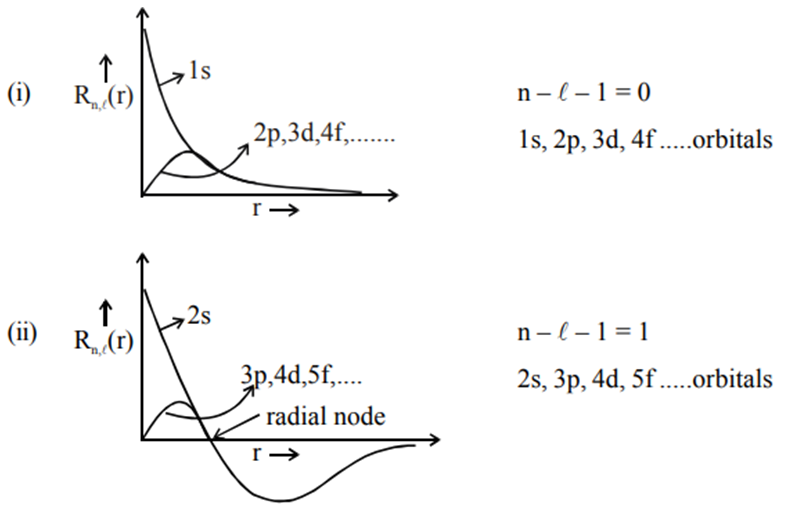
Graph of Radial Probability Density Function
Graph of Radial Probability Density Function : The graph of the radial probability density function in the Schrödinger wave equation illustrates the likelihood of finding an electron at a given distance from the nucleus in an atom. It typically peaks near the nucleus and decreases as the distance increases, reflecting the decreasing probability of finding the electron farther from the nucleus. This graph provides insights into the spatial distribution of electron density within atoms, essential for understanding atomic properties and chemical behavior.
Graph of Radial Probability Density Function [R 2 (r) or ψ 2 (r)]:
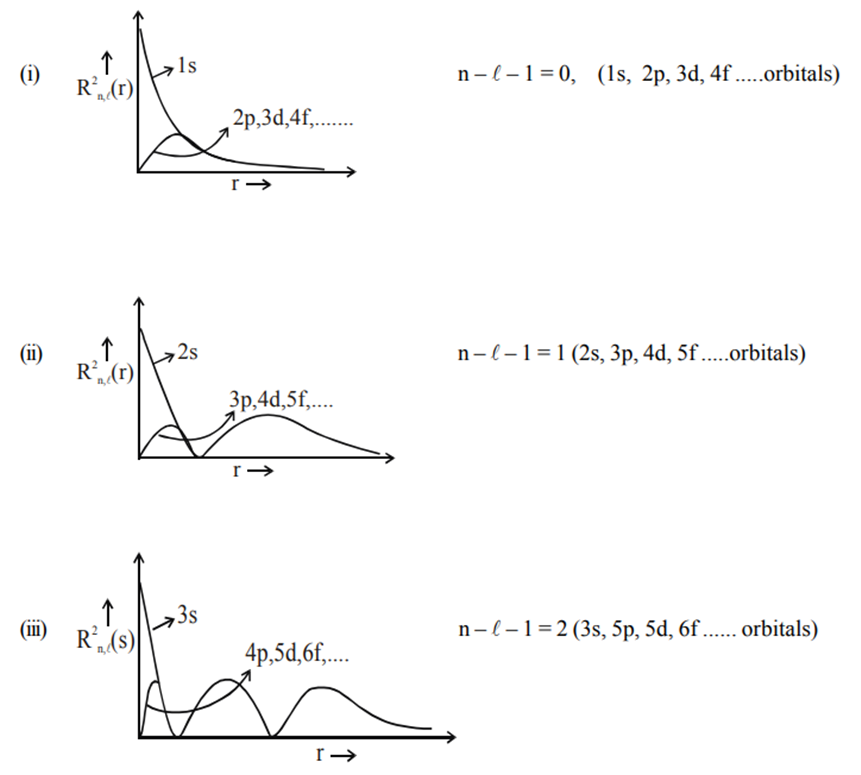
Angular Part of Solution
Angular Part of Solution : In the solution of the Schrödinger wave equation, the angular part describes the spatial orientation of the wave function. It includes factors like spherical harmonics, which specify the angular dependence of the wave function. The angular part determines the shape of atomic orbitals and plays a crucial role in understanding molecular geometry and chemical bonding.
(1) s-orbital
∙ As the probability of finding electron is not depending on angle (direction) then it must be same. In all direction and hence the shape of s-orbital is spherical.
(2) p-orbital
(3) d-orbital
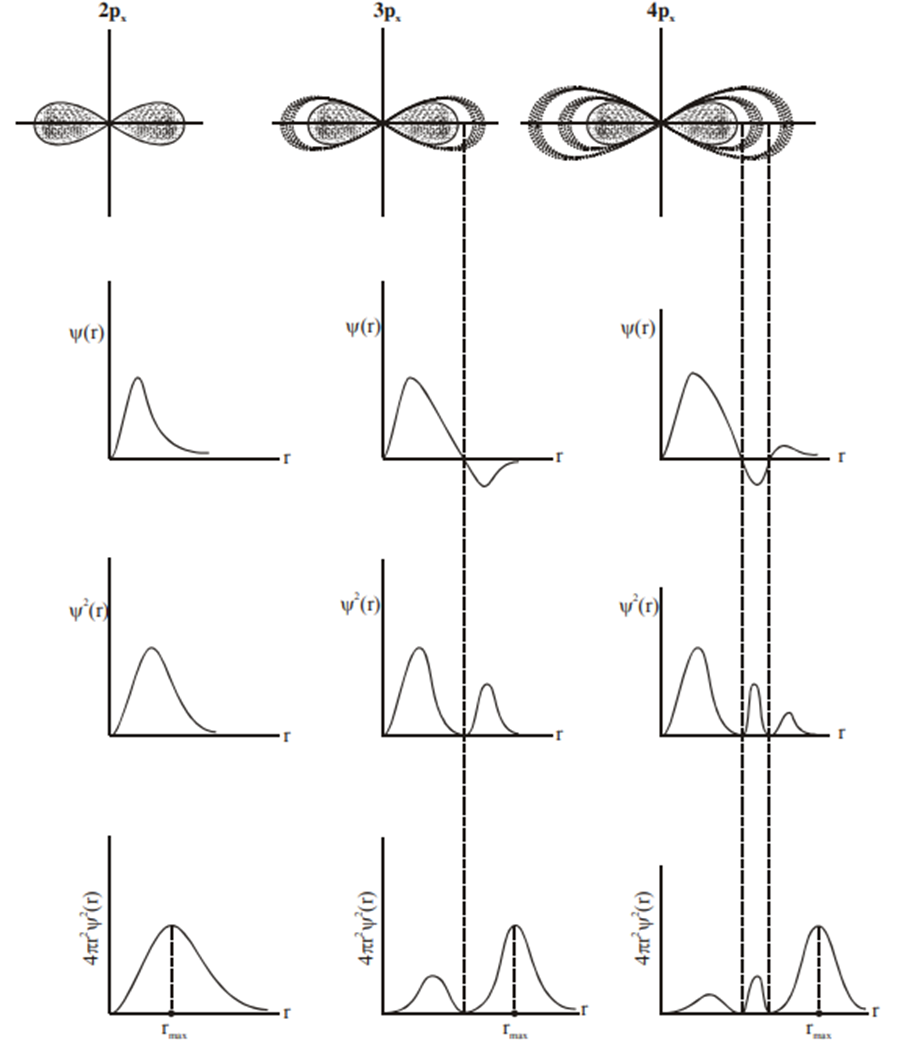
Electron-density distribution
Electron-density distribution in 1s, 2s and 3s-orbitals:
The lower part of the fig. shows how the electron density, represented by
Electron-density distribution in 2p x , 3p x and 4p x -orbital
Schrodinger Wave Equation FAQs
Q.1 : What is the Schrödinger wave equation, and why is it important in quantum mechanics?
Q.2 : What is the radial part of the solution of the Schrödinger wave equation?
Q. 3 : What is the angular part of the solution of the Schrödinger wave equation?
Q.4 : What is the graphical understanding of the solution of the Schrödinger wave equation?
Q.5 : What are some common graphical representations used in studying the solution of the Schrödinger wave equation?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
