Area Under The Curve Formula with Solved Example

Calculating the Area Under the Curve Formula involves various methods, with the antiderivative method being one of the most widely used approaches. Unlike regular geometric shapes for which we have well-defined formulas to calculate areas, finding the area under a curve typically requires knowledge of the curve's equation, the boundaries of the region of interest, and the axis that encloses the curve. The process of integration is a powerful tool for solving equations and determining the required area.

When it comes to finding the areas of irregular plane surfaces, the antiderivative methods are invaluable. In this discussion, we will explore how to calculate the area under a curve in relation to an axis, find the area between a curve and a line, and determine the area between two curves.

How to Find Area Under The Curve Formula?

Calculating the area under the curve involves a straightforward process that can be broken down into three essential steps:

Function and Limits: Start by identifying the equation of the curve, typically represented as y=f(x). Determine the specific interval or limits on the x-axis over which you want to find the area. It's essential to specify the axis that encloses the area of interest.

Integration (Antiderivative): Next, find the antiderivative of the curve's equation, denoted as F(x). This entails performing integration with respect to x on the function f(x). The antiderivative F(x) essentially represents the accumulated area between the curve and the axis.

Apply Limits and Find the Difference: Finally, apply the upper and lower limits of the interval to the antiderivative F(x) and calculate the difference. This subtraction of values at the upper and lower limits yields the area under the curve within the specified interval.

Mathematically, this process can be expressed as follows:

Different Methods to Find Area Under The Curve Formula

Method I: Riemann Sums

In this method, the area under the curve is divided into the smallest possible rectangles. The total area under the curve is obtained by summing the areas of these rectangles. For a curve represented by

y=f(x), it is divided into numerous rectangles, each having a width of δx. As the number of rectangles approaches infinity (n→∞), the formula for the total area under the curve is given by:

A represents the total area under the curve, n is the number of rectangles and represents the function's value at a specific point

Method II: Approximation with Rectangles

This method also involves dividing the area under the curve into rectangles, but here, only a limited number of rectangles are used. The areas of these rectangles are added together to provide an approximation of the total area under the curve. While this method is simpler, it offers only an approximate value for the area under the curve.

Also Read – Comparing Quantities Formula

Formula For Area Under the Curve

The area under a curve can be calculated with respect to different axes, using the axes as boundaries for the given curve. Specifically, we can calculate the area under the curve with respect to the x-axis or y-axis, depending on the orientation of the curve. There are cases where the curve lies entirely below the axes, as well as cases where the curve partially extends below the axes. For all these scenarios, we have derived formulas to determine the area under the curve.

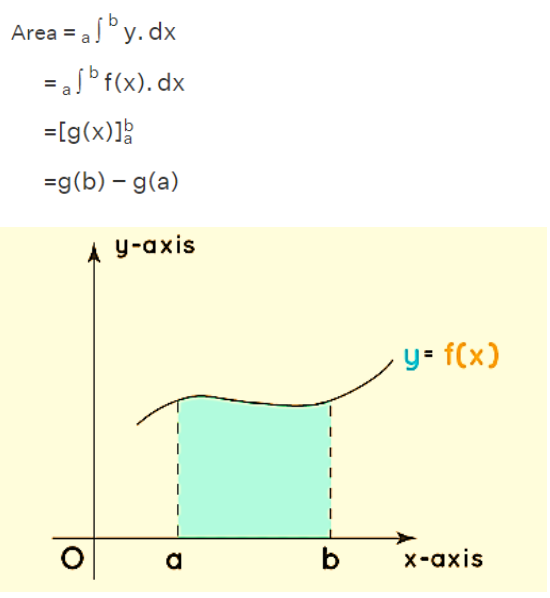
Area with Respect to the X-axis: Let's begin by examining the area enclosed by the curve

y=f(x) and the x-axis. The following figures illustrate the area enclosed by the curve and the x-axis. The boundaries for the curve with respect to the x-axis are denoted as a and b. The formula to calculate the area under the curve with respect to the x-axis is as follows:

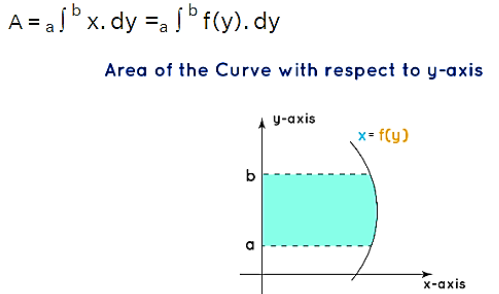
Area with respect to the y-axis: The area of the curve bounded by the curve x = f(y), the y-axis, across the given lines y = a and y = b is represented by the following expression below. Moving forward, the area between the curve and the y-axis can be understood from the below graph.

Also Read – Cubes and Cubes Roots Formula

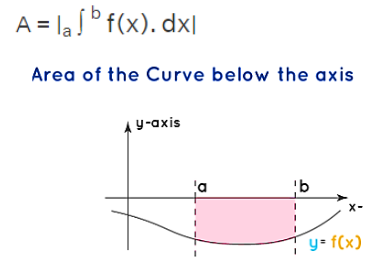
Area Below the X-axis: When calculating the area of a curve that lies below the X-axis, it's important to note that this area is considered negative. To obtain the magnitude or absolute value of this negative area, we take the modulus (absolute value) of the result.

For a curve defined by y=f(x) that lies below the x-axis and is bounded by the x-axis, with limits a and b, the formula for finding the absolute area between the curve and the x-axis is as follows:

Area Above and Below the Axis : When dealing with a curve that extends both above and below the axis, the total area enclosed by the curve is calculated by separately finding the areas above and below the axis. It's essential to keep in mind that the area below the axis is considered negative, so the modulus (absolute value) of this area is taken to obtain its magnitude.

Therefore, the overall area enclosed by the curve is equal to the sum of these two areas: the positive area above the axis and the absolute value of the negative area below the axis. Mathematically, this can be expressed as:

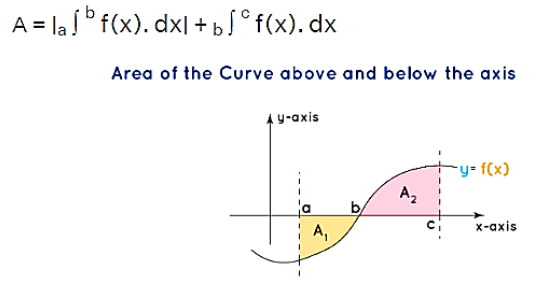
Also Check – Algebra Formulas

Area Under the Curve Formula

Type of Area	Formula of Area
Area Using Riemanns Sum
Area with Respect to y-axis
Area with respect to x-axis
Area under parabola	2∫ab√(4ax).dx
Area under Circle	4∫ab√(a2 – x2).dx
Area under Ellipse	4b/a∫ab√(a2 – x2).dx