
Algebra Formula are the fundamental building blocks for many mathematical topics. These encompass equations, quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, and probability, which heavily rely on algebraic formulas for comprehension and solving intricate problems. Algebraic formulas are invaluable tools for swiftly performing complex calculations with minimal steps. They are also instrumental in simplifying algebraic expressions.
Variety Of Algebraic Formulas
The world of algebraic formulas expands by the complexity of mathematical subjects. Specialized sets of algebraic formulas are designated for logarithms, indices, exponents, progressions, permutations, and combinations. Below is an extensive list of algebraic formulas spanning various mathematical domains.
Algebra Formulas - Identities
In algebraic formulas, an identity signifies an equation that remains true irrespective of the assigned variable values. An algebraic identity demonstrates that the left-hand side is identical to the right-hand side for all variable values. These identities play a pivotal role in determining the values of unknown variables. Here are a few algebraic identities that are often used:
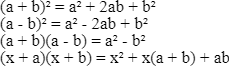
Also Check - Rational Numbers Formulas
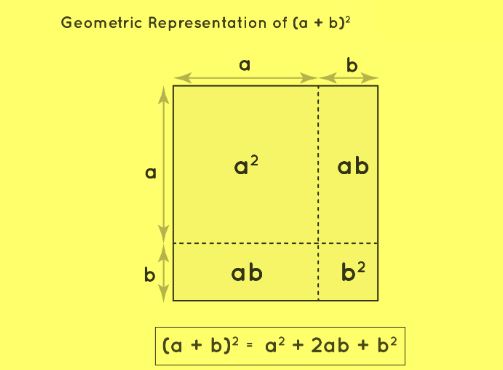
Now explore the algebraic identity (a + b)² = a² + 2ab + b² and its algebraic and geometrical significance. We can establish the proof of this formula by multiplying the expression algebraically:
Geometrically, this expression can be understood as the area of four sub-figures within a square diagram. We can further consolidate the proof of the identity (a + b)² = a² + 2ab + b².
Also Read - Linear Equation Formula
Similarly, other algebraic identities can be proven using squares and rectangles.
What Are Algebra Formulas?
An algebraic formula is a mathematical equation or rule that uses symbols and terms. It typically involves algebraic expressions on both sides. Algebraic formulas serve as concise methods for solving complex algebraic calculations. These formulas can be derived for various mathematical topics, typically involving an unknown variable denoted as 'x.' Standard algebraic formulas can be applied across diverse mathematical domains.
For instance, (a + b)² = a² + 2ab + b² is an algebraic formula, where:
(a + b)² is an algebraic expression
a² + 2ab + b² is the simplified form of the algebraic expression
Let's organize these algebraic formulas by class:
Algebraic Formulas for Class 8
Algebraic Formulas for Class 9
Algebraic Formulas for Class 10
Algebraic Formulas for Class 11
Algebraic Formulas for Class 12
Algebra Formulas For Class 8
In Class 8, algebraic formulas are introduced for three variables (a, b, and c) and a maximum degree of 3. These formulas can be derived by multiplying the expression by itself based on the exponent value. Here are some Class 8 algebraic formulas:
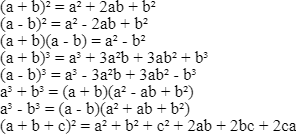
Laws of Exponents
Algebraic formulas also encompass laws of exponents, which are crucial for simplifying complex exponential terms. These laws are beneficial for handling higher exponential values and deriving certain logarithmic laws. The fundamental laws of exponents include:
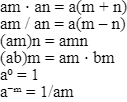
Each of these laws serves a specific purpose and plays a vital role in algebraic calculations.
Algebra Formulas for Class 9
Class 9 introduces logarithms, which are instrumental in handling highly complex multiplication and division calculations. Logarithmic equations provide an alternative representation for exponential expressions. The properties of logarithms are essential in logarithmic calculations. The key logarithmic algebraic formulas include:
logₐ(xy) = logₐx + logₐy
logₐ(x/y) = logₐx - logₐy
logₐxⁿ = n ⋅ logₐx
logₐa = 1
logₐ1 = 0
Algebra Formulas for Class 10
Class 10 introduces the quadratic formula, a pivotal concept in algebra. The typical format for a quadratic equation is ax² + bx + c = 0, and you can solve it by using algebraic techniques or applying the quadratic formula. The quadratic formula expedites the determination of variable values with minimal steps. The quadratic formula is:
In this formula, b² - 4ac is known as the discriminant, which determines the nature of the equation's roots:
If b² - 4ac > 0, the quadratic equation has two distinct real roots.
If b² - 4ac = 0, the quadratic equation has two equal real roots.
If b² - 4ac < 0, the quadratic equation has two imaginary roots.
Additionally, Class 10 covers formulas related to progressions, including arithmetic and geometric sequences. These formulas are essential for finding the nth term and the sum of terms in these sequences:
Arithmetic Sequence Formulas:
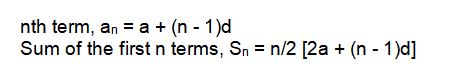 Geometric Sequence Formulas:
Geometric Sequence Formulas:
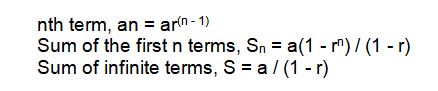
Algebra Formulas for Class 11
In Class 11, algebraic formulas play a significant role in two key areas: permutations and combinations. These concepts help us arrange and group items differently, and specific formulas assist in their calculations.
Permutation Formulas
Permutations arrange 'r' items from a set of 'n' items in various orders. To calculate permutations, we use these formulas:
Combination Formulas
Combinations focus on selecting 'r' items from a set of 'n' items without considering their order. The relevant formulas are:
nCr Formula: n C r (or) n C r = n! / [r!(n - r)!]
Apart from permutations and combinations, Class 11 introduces the "Binomial Theorem," a vital tool for handling algebraic expressions with two terms raised to large exponents. This theorem uses coefficients derived from combination formulas to expand binomial expressions. Here's the comprehensive formula for binomial expansion, known as the algebraic expression of the binomial theorem:
Binomial expansion algebraic formula
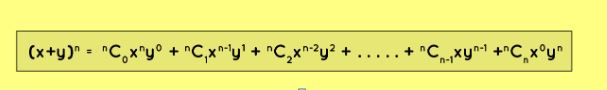
This formula is beneficial for simplifying complex expansions like (x + 2y)7, (3x - y)11, and more.
Class 12 Algebra Formula
In Class 12, algebraic formulas extend to vector algebra, introducing mathematical concepts involving vectors 'a,' 'b,' and 'c':
The magnitude of vector 'a' = x i + y j + z k is calculated as |a| = √(x² + y² + z²).
The unit vector along 'a' is a/|a|.
The dot product between vectors 'a' and 'b' is a ⋅ b = |a| |b| cos θ, where θ represents the angle between vectors 'a' and 'b.'
The cross product of vectors 'a' and 'b' is defined as: a × b = |a| |b| sin θ, with θ being the angle between the vectors.
The scalar triple product of three vectors, 'a,' 'b,' and 'c,' is given by
[a b c ] = a ⋅ (b × c) = (a × b) ⋅ c.
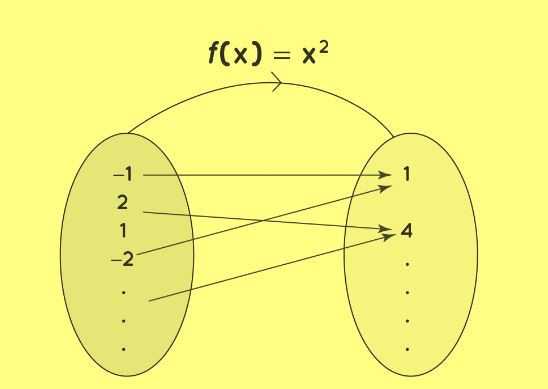
Algebraic Functions
Algebraic functions are represented in y = f(x), where 'x' is the input, and 'y' corresponds to the output. While each input yields a single output, multiple inputs can map to the same output. For example, f(x) = x² represents an algebraic function, where, for x = 2, f(2) = 2² = 4. Here, 'x = 2' is the input, and 'f(2) = 4' is the output.
Algebraic Fractions
In algebra, fractions are rational expressions following the same arithmetic rules as numerical fractions. These fractions involve unknown variables and adhere to the standard rules for working with fractions. Here are four essential expressions for handling algebraic fractions:
Adding Fractions: x/y + z/w = (xw + yz)/(yw)
Subtracting Fractions: x/y - z/w = (xw - yz)/(yw)
Multiplying Fractions: x/y × z/w = xz/yw
Dividing Fractions: x/y ÷ z/w = x/y × w/z = xw/yz
Challenging Questions on Algebra Formulas
To reinforce your understanding of algebraic expressions further, consider tackling these challenging questions:
Quadratic Equation Roots: Find the roots of the quadratic equation: x² + 7x + 12 = 0.
Simplifying Algebraic Expression: Simplify the expression (x - 9y³)/(x - 7y⁸) so that the answer contains no negative exponents.
Logarithmic Expansion: Expand the logarithm: log(x²y³z).
Algebra Formula FAQs
What are algebraic formulas?
Why are algebraic identities important?
What are the fundamental laws of exponents?
What is the quadratic formula used for?
What is the discriminant in the quadratic formula?










