
NCERT Solutions For Class 11 Chemistry chapter 5-States Of Matter
NCERT Solutions for class-11 Chemistry Chapter 5 States of Matter is prepared by our senior and renown teachers of Physics Wallah primary focus while solving these questions of class-11 in NCERT textbook, also do read theory of this Chapter 5 States of Matter while going before solving the NCERT questions. Our Physics Wallah team Prepared Other Subjects NCERT Solutions for class 11.
Chapter 5 States of Matter
Answer the following Questions.
1. What will be the minimum pressure required to compress 500 dm
3
of air at 1 bar to 200 dm
3
at 30°C?
Solution :
Given,
Initial pressure, P
1
= 1 bar
Initial volume, V
1
= 500 dm
3
Final volume, V
2
= 200 dm
3
Since the temperature remains constant, the final pressure (P
2
) can be calculated using Boyle's law.
According to Boyle's law,
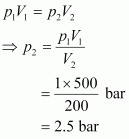
2. A container with a capacity of 120 mL contains some amount of gas at 35∘ C and 1.2 bar pressure. The gas is transferred to another container of volume 180 mL at 35∘C. Calculate what will be the pressure of the gas?
Solution :
Initial pressure, P
1
= 1.2 bar
Initial volume, V
1
= 120 mL
Final volume, V
2
= 180 mL
As the temperature remains same, final pressure (P
2
) can be calculated with the help of Boyle’s law.
According to the Boyle’s law,
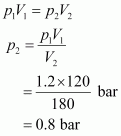
Therefore, the min pressure required is 0.8 bar.
3. Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressurep.
Solution :
The equation of state is given by,
pV = nRT ……….. (i)
Where,
p → Pressure of gas
V → Volume of gas
n→ Number of moles of gas
R → Gas constant
T → Temperature of gas
From equation (i) we have,
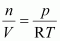
Replacing n with m/M, we have
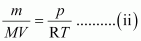
Where,
m → Mass of gas
M → Molar mass of gas
But, m/v= d (d = density of gas)
Thus, from equation (ii), we have
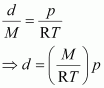
Molar mass (M) of a gas is always constant and therefore, at constant temperature=
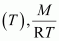 constant.
constant.
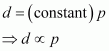
Hence, at a given temperature, the density (d) of gas is proportional to its pressure (p).
4. At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?
Solution :
Density (d) of the substance at temperature (T) can be given by the expression,
d =
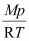
Now, density of oxide (d
1
) is given by,
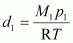
Where, M
1
and p
1
are the mass and pressure of the oxide respectively.
Density of dinitrogen gas (d
2
) is given by,
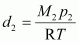
Where, M
2
and p
2
are the mass and pressure of the oxide respectively.
According to the given question,
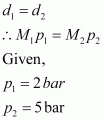
Molecular mass of nitrogen, M
2
= 28 g/mol
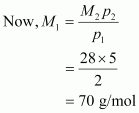
Hence, the molecular mass of the oxide is 70 g/mol.
5. Pressure of 1 g of an ideal gas A at 27 °C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature the pressure becomes 3 bar. Find a relationship between their molecular masses.
Solution :
For ideal gas A, the ideal gas equation is given by,
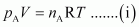
Where, p
A
and n
A
represent the pressure and number of moles of gas A.
For ideal gas B, the ideal gas equation is given by,
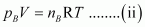
Where, p
B
and n
B
represent the pressure and number of moles of gas B.
[V and T are constants for gases A and B]
From equation (i), we have
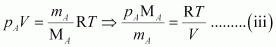
From equation (ii), we have
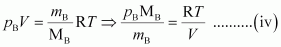
Where, M
A
and M
B
are the molecular masses of gases A and B respectively.
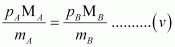
Now, from equations (iii) and (iv), we have
Given,
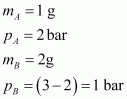
(Since total pressure is 3 bar)
Substituting these values in equation (v), we have
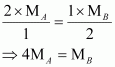
Thus, a relationship between the molecular masses of A and B is given by.
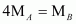
6. The drain cleaner, Drainex contains small bits of aluminum which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20 °C and one bar will be released when 0.15g of aluminum reacts?
Solution :
The reaction of aluminium with caustic soda can be represented as:
At STP (273.15 K and 1 atm), 54 g (2 × 27 g) of Al gives 3 × 22400 mL of H
2
..
0.15 g Al gives i.e., 186.67 mL of H
2
.
At STP,
Let the volume of dihydrogen be at p
2
= 0.987 atm (since 1 bar = 0.987 atm) and T
2
= 20°C = (273.15 + 20) K = 293.15 K..
Therefore, 203 mL of dihydrogen will be released.
7. What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3 flask at 27 °C ?
Solution :
It is known that,
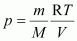
For methane (CH
4
),
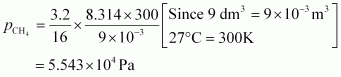
For carbon dioxide (CO
2
),
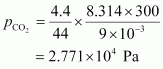
Total pressure exerted by the mixture can be obtained as:
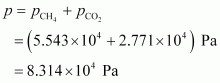
Hence, the total pressure exerted by the mixture is 8.314 × 104 Pa.
8. What will be the pressure of the gaseous mixture when 0.5 L of H
2
at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1L vessel at 27°C?
Solution :
Let the partial pressure of H
2
in the vessel be.
Now,
 = ?
= ?

It is known that,
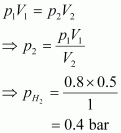
Now, let the partial pressure of O
2
in the vessel be.
p
1
V
1
= p
2
V
2
⇒p
2
=p
1
V
1
/V2
⇒pO
2
=0.7×2 .0 /1= 1.4 bar
Total pressure of the gas mixture in the vessel can be obtained as:
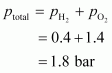
Hence, the total pressure of the gaseous mixture in the vessel is.
9. Density of a gas is found to be 5.46 g /dm
3
at 27 °C at 2 bar pressure. What will be its density at STP?
Solution :
Given,
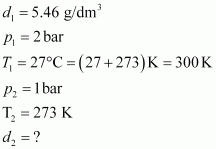
The density (d
2
) of the gas at STP can be calculated using the equation,
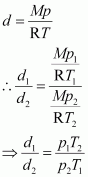
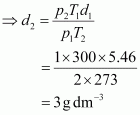
Hence, the density of the gas at STP will be 3 g dm
–3
.
10. 34.05 mL of phosphorus vapour weighs 0.0625 g at 546
°
C and 0.1 bar pressure. What is the molar mass of phosphorus?
Solution :
Given,
p = 0.1 bar
V = 34.05 mL = 34.05 × 10
–3
L = 34.05 × 10
–3
dm
3
R = 0.083 bar dm
3
K
–1
mol
–1
T = 546°C = (546 + 273) K = 819 K
The number of moles (n) can be calculated using the ideal gas equation as:
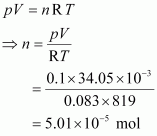
Therefore, molar mass of phosphorus
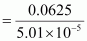 = 1247.5 g mol
–1
= 1247.5 g mol
–1
Hence, the molar mass of phosphorus is 1247.5 g mol
–1
.
11. A student forgot to add the reaction mixture to the round bottomed flask at 27 °C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer he found the temperature of the flask was 477 °C. What fraction of air would have been expelled out?
Solution :
Let the volume of the round bottomed flask be V.
Then, the volume of air inside the flask at 27° C is V.
Now,
V
1
= V
T
1
= 27°C = 300 K
V
2
=?
T
2
= 477° C = 750 K
According to Charles’s law,
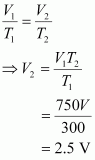
Therefore, volume of air expelled out = 2.5 V – V = 1.5 V
Hence, fraction of air expelled out
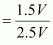 =3/5
=3/5
12. Calculate the temperature of 4.0 mol of a gas occupying 5 dm
3
at 3.32 bar.(R = 0.083 bar dm3 K
–1
mol
–1
).
Solution :
Given,
n = 4.0 mol
V = 5 dm
3
p = 3.32 bar
R = 0.083 bar dm3 K
–1
mol
–1
The temperature (T) can be calculated using the ideal gas equation as:
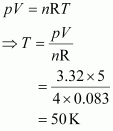
Hence, the required temperature is 50 K.
13. Calculate the total number of electrons present in 1.4 g of dinitrogen gas.
Solution :
Molar mass of dinitrogen (N
2
) = 28 g mol
–1
Thus, 1.4 g of
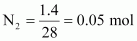
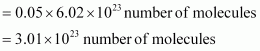
Now, 1 molecule of contains 14 electrons.
Therefore, 3.01 × 10
23
molecules of N
2
contains = 1.4 × 3.01 × 1023
= 4.214 × 10
23
electrons
14. How much time would it take to distribute one Avogadro number of wheat grains, if 10
10
grains are distributed each second?
Solution :
Avogadro number = 6.02 × 10
23
Thus, time required
=
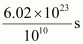
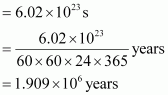
Hence, the time taken would be
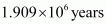 .
.
15. Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm3 at 27°C. R = 0.083 bar dm3 K
–1
mol
–1
.
Solution :
Given,
Mass of dioxygen (O
2
) = 8 g
Thus, number of moles of
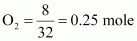
Mass of dihydrogen (H
2
) = 4 g
Thus, number of moles of
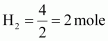
Therefore, total number of moles in the mixture = 0.25 + 2 = 2.25 mole
Given,
V = 1 dm
3
n = 2.25 mol
R = 0.083 bar dm3 K
–1
mol
–1
T = 27°C = 300 K
Total pressure (p) can be calculated as:
pV = nRT
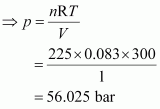
Hence, the total pressure of the mixture is 56.025 bar.
16. Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10 m, mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 1.2 kg m
–3
and R = 0.083 bar dm3 K
–1
mol
–1
).
Solution :
Given,
Radius of the balloon, r = 10 m
Volume of the balloon
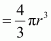
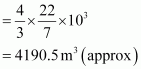
Thus, the volume of the displaced air is 4190.5 m
3
.
Given,
Density of air = 1.2 kg m
–3
Then, mass of displaced air = 4190.5 × 1.2 kg
= 5028.6 kg
Now, mass of helium (m) inside the balloon is given by,

Now, total mass of the balloon filled with helium = (100 + 1117.5) kg
= 1217.5 kg
Hence, pay load = (5028.6 – 1217.5) kg
= 3811.1 kg
Hence, the pay load of the balloon is 3811.1 kg.
17. Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol
–1
.
Solution :
It is known that,
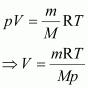
Here,
m = 8.8 g
R = 0.083 bar LK
–1
mol
–1
T = 31.1°C = 304.1 K
M = 44 g
p = 1 bar
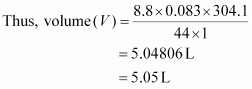
Hence, the volume occupied is 5.05 L.
18. 2.9 g of a gas at 95 °C occupied the same volume as 0.184 g of dihydrogen at 17 °C, at the same pressure. What is the molar mass of the gas?
Solution :
Volume (V) occupied by dihydrogen is given by,
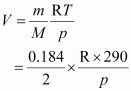
Let M be the molar mass of the unknown gas. Volume (V) occupied by the unknown gas can be calculated as:
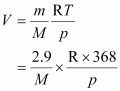
According to the question,
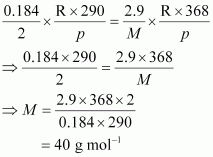
Hence, the molar mass of the gas is 40 g mol
–1
.
19. A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.
Solution :
Let the weight of dihydrogen be 20 g and the weight of dioxygen be 80 g.
Then, the number of moles of dihydrogen,
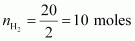 and
and
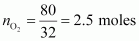 the number of moles of dioxygen, .
the number of moles of dioxygen, .
Given,
Total pressure of the mixture, p
total
= 1 bar
Then, partial pressure of dihydrogen,
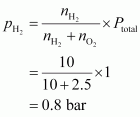
Hence, the partial pressure of dihydrogen is.
20. What would be the SI unit for the quantity pV
2
T
2
/n?
Solution :
The SI unit for pressure, p is Nm
–2
.
The SI unit for volume, V is m
3
.
The SI unit for temperature, T is K.
The SI unit for the number of moles, n is mol.
Therefore, the SI unit for quantity
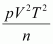 is given by,
is given by,
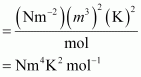
21. In terms of Charles’ law explain why –273°C is the lowest possible temperature.
Solution :
Charles’ law states that at constant pressure, the volume of a fixed mass of gas is directly proportional to its absolute temperature.
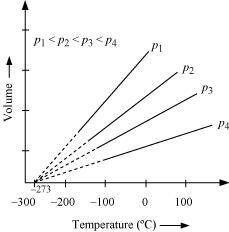
It was found that for all gases (at any given pressure), the plots of volume vs. temperature (in °C) is a straight line. If this line is extended to zero volume, then it intersects the temperature-axis at – 273°C. In other words, the volume of any gas at –273°C is zero. This is because all gases get liquefied before reaching a temperature of – 273°C. Hence, it can be concluded that – 273°C is the lowest possible temperature.
22. Critical temperature for carbon dioxide and methane are 31.1 °C and –81.9 °C respectively. Which of these has stronger intermolecular forces and why?
Solution :
Higher is the critical temperature of a gas, easier is its liquefaction. This means that the intermolecular forces of attraction between the molecules of a gas are directly proportional to its critical temperature. Hence, intermolecular forces of attraction are stronger in the case of CO2.
23. Explain the physical significance of Van der Waals parameters.
Solution :
Physical significance of ‘a’:
‘a’ is a measure of the magnitude of intermolecular attractive forces within a gas.
Physical significance of ‘b’:
‘b’ is a measure of the volume of a gas molecule.
NCERT Solutions For Class 11 Chemistry Chapter Wise.









