
Arctan Formula In the realm of trigonometry, "arctan" denotes the inverse tangent function. When dealing with inverse trigonometric functions, the prefix "arc" is commonly employed. Mathematically, we symbolize the inverse tangent function as "tan (-1) x" or "arctan(x)." Much like the six primary trigonometric functions, there exist six corresponding inverse trigonometric functions:
"sin (-1) x," "cos (-1) x," "tan (-1) x," "csc (-1) x," "sec (-1) x," and "cot (-1) x."
It's essential to note that "arctan" (or "tan (-1) x") is not equivalent to "1 / tan x." In other words, an inverse trigonometric function should not be confused with the reciprocal of its corresponding trigonometric function. The primary purpose of "arctan" is to determine the value of an unknown angle based on the given value of the tangent trigonometric ratio. Applications of the "arctan" function are widespread, particularly in navigation, physics, and engineering.
In this article, we will delve into various aspects of "tan (-1) x," including its domain, range, and graphical representation, as well as its integral and derivative values.
What Is Arctan?
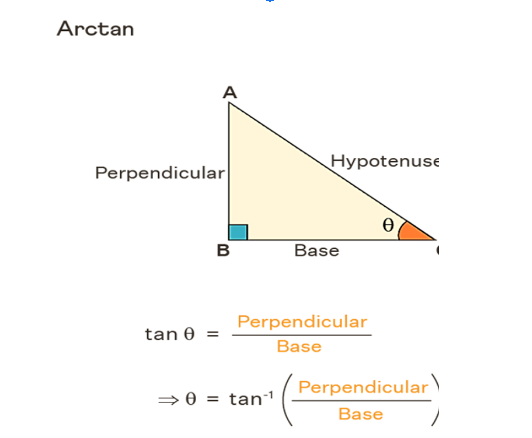
Arctan holds a significant place among the inverse trigonometric functions. In the context of a right-angled triangle, the tangent of an angle defines the ratio of the perpendicular side to the base side, expressed as "Perpendicular / Base." Conversely, when we take the arctan of the "Perpendicular / Base" ratio, it yields the value of the corresponding angle between the base and the hypotenuse. In essence, arctan acts as the inverse operation to the tangent function.
To illustrate how the arctan function operates, consider the following examples:
- When tan(π / 2) equals ∞, we find that arctan(∞) equals π/2.
- If tan (π / 3) is equal to √3, then arctan(√3) equals π/3.
- In the case of tan(0) being equal to 0, arctan(0) equals 0.
Now, envision a scenario where we have a right-angled triangle, and we seek to determine the value of an angle denoted as θ. We are aware that tan θ is equivalent to the ratio of the perpendicular side to the base side, represented as tan θ = Perpendicular / Base. To ascertain the value of θ, we employ the arctan function, expressed as θ = tan (-1)
Arctan Formula
As previously mentioned, the fundamental formula for arctan is expressed as follows: arctan (Perpendicular/Base) = θ, where θ represents the angle formed between the hypotenuse and the base within a right-angled triangle. This formula for arctan serves as a means to determine the value of angle θ, whether in degrees or radians. Alternatively, we can represent this formula as θ = tan (-1) [Perpendicular / Base].
Arctan Identities
Numerous arctan formulas, identities, and properties play a crucial role in tackling both straightforward and intricate problems in inverse trigonometry. Here are a few of these essential mathematical tools:
- arctan(-x) = -arctan(x), for all x ∈ R
- tan (arctan x) = x, for all real numbers x
- arctan (tan x) = x, for x ∈ (-π/2, π/2)
- arctan(1/x) = π/2 - arctan(x) = arccot(x), if x > 0 or, arctan(1/x) = - π/2 - arctan(x) = arccot(x) - π, if x < 0
- sin(arctan x) = x / √(1 + x 2 )
- cos(arctan x) = 1 / √(1 + x 2 )
- π/4 = 4 arctan(1/5) - arctan(1/239)
- π/4 = arctan(1/2) + arctan(1/3)
- π/4 = 2 arctan(1/2) - arctan(1/7)
- π/4 = 2 arctan(1/3) + arctan(1/7)
- π/4 = 8 arctan(1/10) - 4 arctan(1/515) - arctan(1/239)
- π/4 = 3 arctan(1/4) + arctan(1/20) + arctan(1/1985)
How To Apply Arctan x Formula?
We can gain a more comprehensive grasp of how the arctan formula is applied through the following illustrative instances:
Illustration: Within the context of a right-angled triangle ABC, with a base measuring 2 units and a height of 3 units, we aim to determine the base angle.
Resolution:
To determine the base angle, we apply the arctan formula, as follows:
⇒ θ = arctan(3 ÷ 2) = arctan(1.5)
⇒ θ = 56.3°
Result: The base angle measures 56.3°.
Arctan Domain And Range
All trigonometric functions, including tan(x), exhibit a many-to-one relationship. However, the existence of an inverse function is contingent on it having a one-to-one and surjective (onto) relationship. Consequently, the domain of tan(x) must be restricted to enable the existence of its inverse. In simpler terms, we wish to obtain a single, unique value from the inverse trigonometric function.
To achieve this, the domain of tan(x) is restricted to the interval (-π/2, π/2), excluding values where cos(x) equals 0. The range of tan(x), on the other hand, encompasses all real numbers. It's important to note that the domain and range of a trigonometric function switch roles when dealing with its inverse counterpart. Consequently, for tan (-1) x (arctan), the domain comprises all real numbers, while the range is confined to (-π/2, π/2).
An intriguing aspect worth mentioning is that we can extend the arctan function to complex numbers. In such instances, the domain of arctan expands to encompass all complex numbers.
Arctan Table
Any angle that is provided in degrees can be equivalently expressed in radians by multiplying the degree measurement by the conversion factor of π/180°. Additionally, the arctan function accepts real numbers as input and yields the corresponding unique angle value as output. Below is a table illustrating arctan angle values for various real numbers, which can be employed when plotting the arctan graph.
| x | arctan(x) (°) | arctan(x) (rad) |
| -∞ | -90° | -π/2 |
| -3 | -71.565° | -1.2490 |
| -2 | -63.435° | -1.1071 |
| -√3 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -1/√3 | -30° | -π/6 |
| -1/2 | -26.565° | -0.4636 |
| 0 | 0° | 0 |
| 1/2 | 26.565° | 0.4636 |
| 1/√3 | 30° | π/6 |
| 1 | 45° | π/4 |
| √3 | 60° | π/3 |
| 2 | 63.435° | 1.1071 |
| 3 | 71.565° | 1.2490 |
| ∞ | 90° | π/2 |
Arctan x Properties
Here are some valuable arctan identities derived from the properties of the arctan function. These formulas serve to simplify complex trigonometric expressions, enhancing the ease of problem-solving:
- tan (tan -1 x) = x, for all x
- tan -1 x + tan -1 y = tan -1 [(x + y)/(1 - xy)], when xy < 1 tan -1 x - tan -1 y = tan -1 [(x - y)/(1 + xy)], when xy > -1
- We have 3 formulas for 2tan -1 x 2tan -1 x = sin -1 (2x / (1+x 2 )), when |x| ≤ 1 2tan -1 x = cos -1 ((1-x 2 ) / (1+x 2 )), when x ≥ 0 2tan -1 x = tan -1 (2x / (1-x 2 )), when -1 < x < 1
- tan -1 (-x) = -tan -1 x, for all x ∈ R
- tan -1 (1/x) = cot -1 x, when x > 0
- tan -1 x + cot -1 x = π/2, when x ∈ R
- tan -1 (tan x) = x, only when x ∈ R - {x : x = (2n + 1) (π/2), where n ∈ Z} i.e., tan -1 (tan x) = x only when x is NOT an odd multiple of π/2. Otherwise, tan -1 (tan x) is undefined.
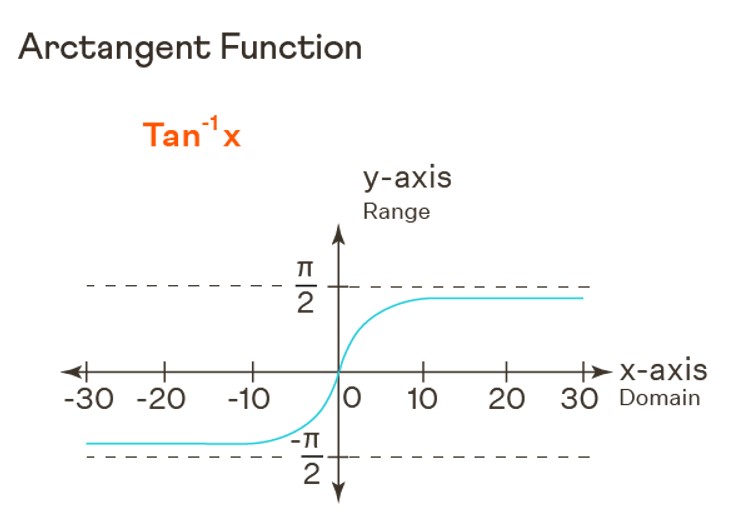
Arctan Graph
Certainly, to create the arctan graph, we should begin by noting that the domain of arctan encompasses all real numbers (R), while its range is confined to the interval (-π/2, π/2). To construct the arctan graph, we can compute several key points by evaluating y = arctan(x). Utilizing the values of well-known special angles, we can establish the following points for the graph:
- When x = ∞, y = π/2.
- When x = √3, y = π/3.
- When x = 0, y = 0.
- When x = -√3, y = -π/3.
- When x = -∞, y = -π/2.
With these points, we can proceed to plot the graph of arctan.
Arctan Derivative
To find the arctan derivative we can use the following algorithm.
Let y = arctan x
Taking tan on both sides we get,
tan y = tan(arctan x)
From the formula, we already know that tan (arctan x) = x
tan y = x
Now on differentiating both sides and employing the chain rule, we get,
sec 2 y dy/dx = 1
⇒ dy/dx = 1 / sec 2 y
According to the trigonometric identity we have sec 2 y = 1 + tan 2 y
dy/dx = 1 / (1 + tan 2 y)
On substitution,
Thus, d(arctan x) / dx = 1 / (1 + x 2 )
Integral Of Arctan x
The antiderivative of the inverse tangent function, arctan(x), is found by employing integration by parts.
Here, f(x) = tan -1 x, g(x) = 1
The formula is given as ∫f(x)g(x)dx = f(x) ∫g(x)dx - ∫[d(f(x))/dx × ∫g(x) dx] dx
On putting the values and solving the expression we get the integral of arctan as,
∫tan -1 x dx = x tan -1 x - ½ ln |1+x 2 | + C
where, C is the constant of integration.
Arctan Formula FAQs
Define the term arctan
Is Arctan the Inverse of Tan?
Define the Arctan at Infinity.
Define the derivative of Arctan.










