The concept of centre of mass (COM) is crucial in physics and engineering. It is a place within or outside an object or system where the entire mass of the object can be concentrated, and the object behaves as if all its mass were concentrated at that point. For a single isolated object, the centre of mass is just the average position of all its constituent particles weighted by their respective masses.

What is Centre of Mass?

The centre of mass of a body or system of particles is defined as a place at which the entire mass of the body or all the masses of a particle system appear to be concentrated. In physics, the centre of mass is defined as a point in space at the centre of the distribution of mass (also known as the balance point), where the weighted relative position of the dispersed mass has a sum of zero. In layman's terms, the centre of mass is a point relative to an item. It is the mean location of a distribution or the average position of all the pieces of the system.

Also Check – Electrical Resistance Formula

Determining of Centre of Mass

We can use gravity forces on the body to experimentally identify a body's centre of mass. This is possible because the centre of mass and the centre of gravity in the parallel gravity field at the earth's surface are the same. Furthermore, the centre of mass of a body with an axis of symmetry and constant density will be on this axis. Similarly, the centre of mass of a circular cylinder with constant density will be on the axis of the cylinder. If we consider a spherically symmetric body with constant density, its COM is located at the middle of the sphere. In principle, the centre of mass of anybody with any symmetry will be a fixed point of that symmetry.

Also Check – Wind Energy Formula

Centre of Mass Formula

The formula to calculate the centre of mass (COM) of a system of 'n' particles with masses ‘ 𝑚 ₁ ‘ 𝑚 ₂ ', ..., ' 𝑚𝑛

', and coordinates ( 𝑥 ₁ , 𝑦 ₁ , 𝑧 ₁ ), ( 𝑥 ₂ , 𝑦 ₂ , 𝑧 ₂ ), ..., ( 𝑥𝑛 , 𝑦𝑛 , 𝑧𝑛 ), respectively, is as follows:

COM 𝑥 = 𝑚 ₁ 𝑥 ₁ + 𝑚 ₂ 𝑥 ₂ +…….+𝑚𝑛𝑥𝑛/ 𝑚 ₁ + 𝑚 ₂ +…..     +𝑚𝑛

COM 𝑦 = 𝑚 ₁ 𝑦 ₁ + 𝑚 ₂ 𝑦 ₂ +…….+𝑚𝑛𝑦𝑛/ 𝑚 ₁ + 𝑚 ₂ +…..     +𝑚𝑛

COM 𝑧 = 𝑚 ₁ 𝑧 ₁ + 𝑚 ₂ 𝑧 ₂ +…….+𝑚𝑛𝑧𝑛/ 𝑚 ₁ + 𝑚 ₂ +…..     +𝑚𝑛

Where:

COM 𝑥 , COM 𝑦 , COM 𝑧

:The 𝑥 , 𝑦 , and 𝑧

coordinates of the centre of mass, respectively.

𝑚 ₁ , 𝑚 ₂ ,………𝑚𝑛

: The masses of the individual particles.

𝑥 ₁ , 𝑦 ₁ , 𝑧 ₁ , 𝑥 ₂ , 𝑦 ₂ , 𝑧 ₂ ,……𝑥𝑛, 𝑦𝑛, 𝑧𝑛

The 𝑥, 𝑦, and 𝑧

coordinates of each individual particle, respectively.

The centre of mass formula represents the weighted average of all particle positions, with the mass of each particle determining its contribution to the total position of the centre of mass. This formula helps us to locate the location in space where we can suppose the total mass of the system is concentrated. The concept of centre of mass simplifies complex system analysis and is essential in understanding the motion and behaviour of objects and systems in numerous domains of physics and engineering.

We can expand the formula to a particle system. The equation can be applied to each axis separately.

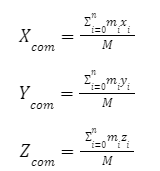
If we have point objects, we can utilise the calculation. If we need to identify the centre of mass of an extended item, such as a rod, we must employ a different approach. We must consider a differential mass and its position before integrating it throughout the entire length.

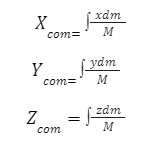
Assume we have a rod, as indicated in the illustration, and we need to determine its centre of mass.

Assume that the entire mass of the rod is M and that the density is uniform. We also suppose that the width of the rod is insignificant, implying that the centre of mass is on the x-axis. We consider a tiny dx away from the origin. Therefore,

𝑑𝑚= 𝑀/ 𝑙 𝑑𝑥

Using the equation to get the centre of mass,

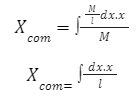
When we integrate it from 0 to l, we obtain

𝑋 _𝑐𝑜𝑚 = 𝑙/ 2

We may find the centre of mass for any geometrical shape using the method described above. You can experiment with a semi-circular ring or a triangle. As a result, if a force is applied to that stretched object, it can be considered to act through the centre of mass and so converted to a point mass.

Also Check – Charge Density Formula

Centre of Mass of a Body Having Continuous Mass Distribution

If the given item is not discrete and their distances are not particular, the centre of mass can be calculated by considering an infinitesimal element of mass (dm) at x, y, and z distances from the origin of the chosen coordinate system.

𝑋 _𝑐𝑜𝑚 = ∫ 𝑥𝑑𝑚/𝑑𝑚

𝑌 _𝑐𝑜𝑚 = ∫ 𝑦𝑑𝑚/ 𝑑𝑚

𝑍 _𝑐𝑜𝑚 = ∫ 𝑧𝑑𝑚/ 𝑑𝑚