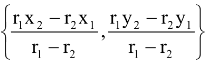Pair of Tangents
Share
Pair of Tangents
Circles of Class 11
Pair of Tangents
Tangents are drawn from P(x 1 , y 1 ) to the circle S = x 2 + y 2 + 2gx + 2fy + c = 0.
The joint equation of the pair of tangents is SS1 = T2 where
S = x 2 + y 2 + 2gx + 2fy + c
S 1 = x 12 + y 12 + 2gx 1 + 2fy 1 + c
and T = xx 1 + yy 1 + g(x + x 1 ) + f(y + y 1 ) + c
Equation of the chord joining two points (acosθ, a sinθ) and (acosφ, asinφ) on the circle x2 + y2 = a2 is
x cos
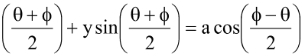
Note that In case θ → φ it becomes a tangent given by
xcosφ + y sinφ = a
External and Internal contacts of circles
Two circles with centers C1(x 1 , y 1 ) and C 2 (x 2 , y 2 ) and radii r 1 , r 2 respectively touch each other.
(a) Externally
If |C
1
C
2
| = r
1
+ r
2
and the point of contact is
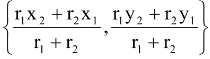
(b) Internally
If |C
1
C
2
| = |r
1
– r
2
| and the point of contact is
