POLYHEDRONS AND NON-POLYHEDRONS SHAPES
Visualising solid shapes of Class 8
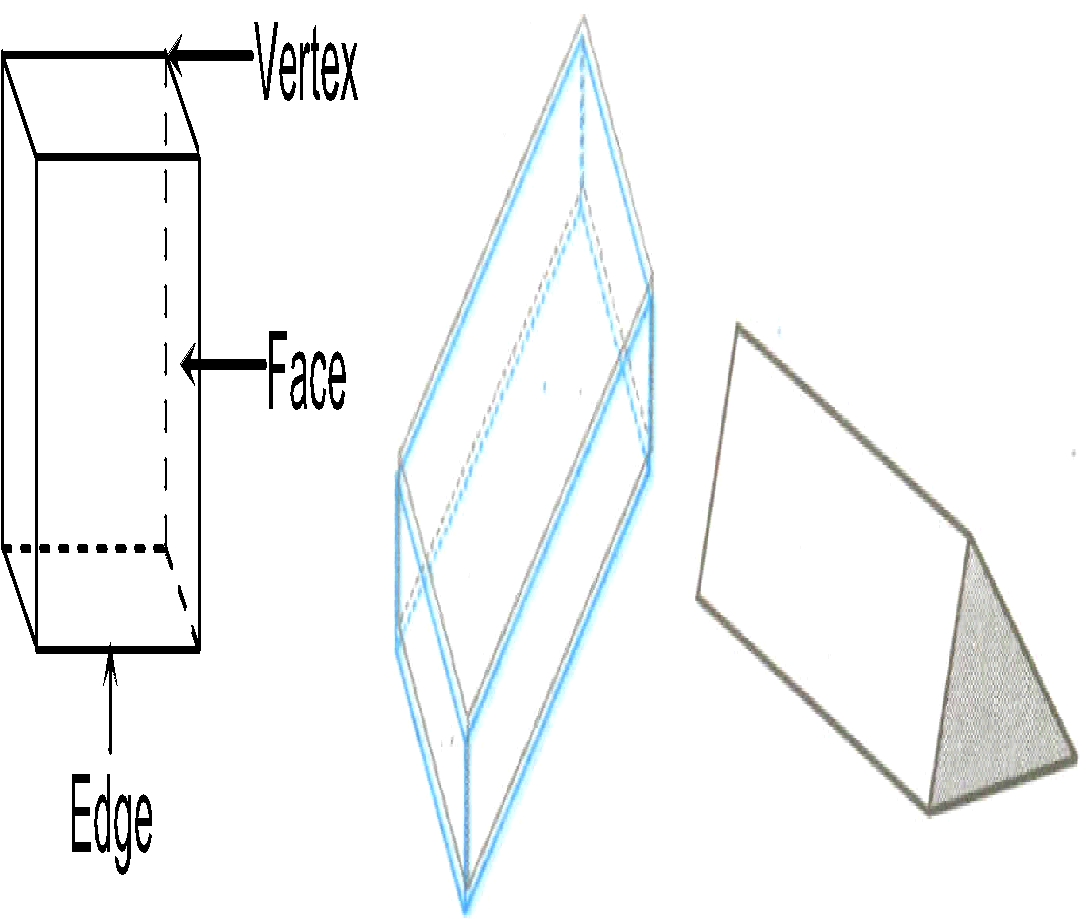
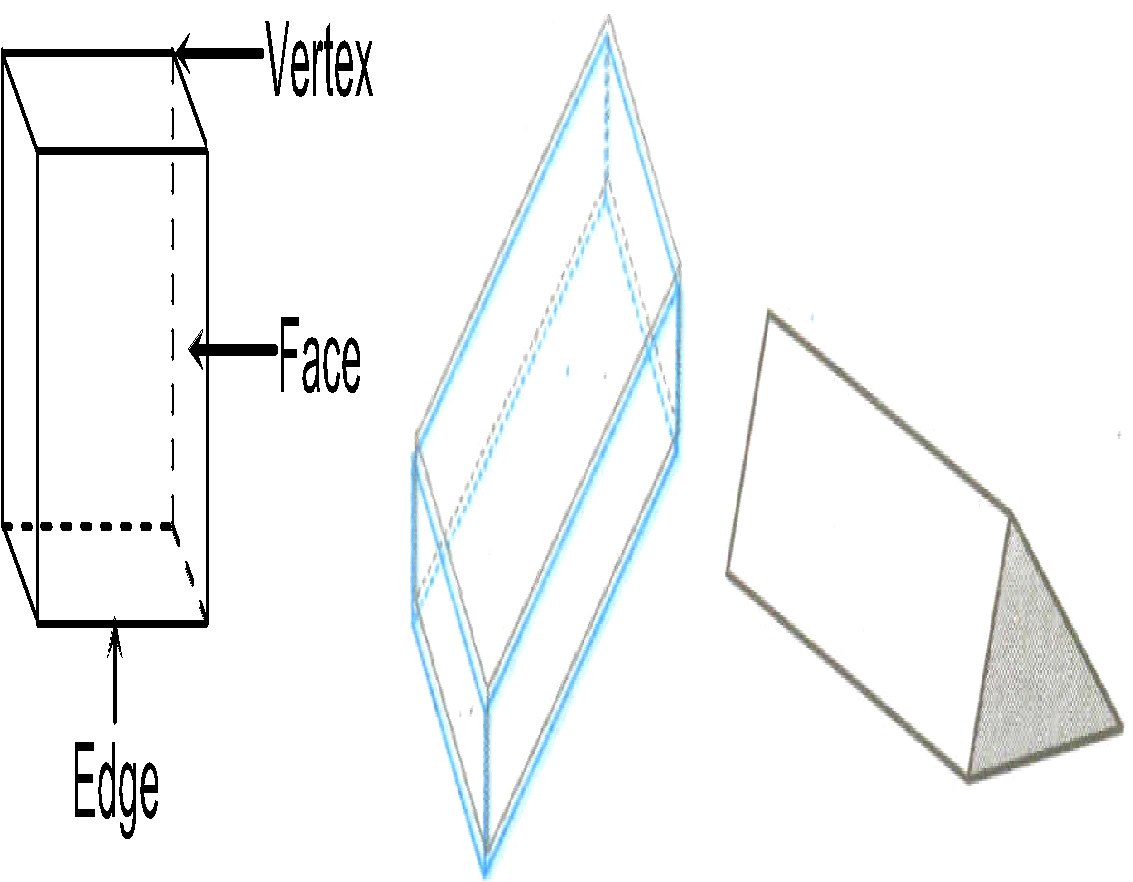
A polyhedron is a geometric solid in three dimensions with flat faces and straight edges.
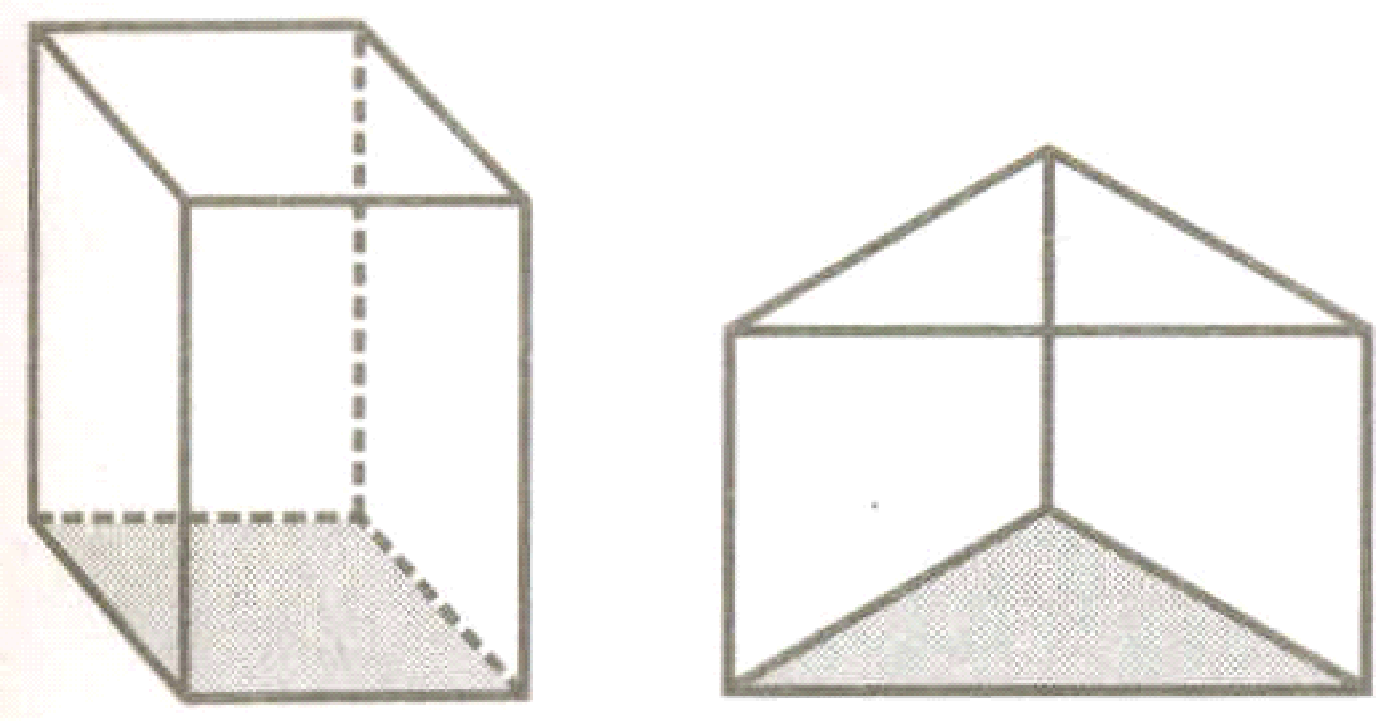
Traingular Prism A Regular Polyhedron
Polyhedral Surface
A defining characteristic of almost all kinds of polyhedra is that just two faces join along any common edge. This ensures that the polyhedral surface is continuously connected and does not end abruptly or split off in different directions.
Edges
Edges have two important characteristics (unless the polyhedron is complex):
- An edge joins just two vertices.
- An edge joins just two faces.
These two characteristics are dual to each other.
Common Polyhedra
|
|
Platonic Solids |
|
|
Prisms |
|
|
Pyramids |
Convex Polyhedrons
The idea of convex polyhedron is similar to that of convex polygons.
|
These are convex
polyhedrons |
These are not convex polyhedrons |
Regular Polyhedrons
A polyhedron is said to be regular if its faces are made up of regular polygons and the same number of faces meet at each vertex.
|
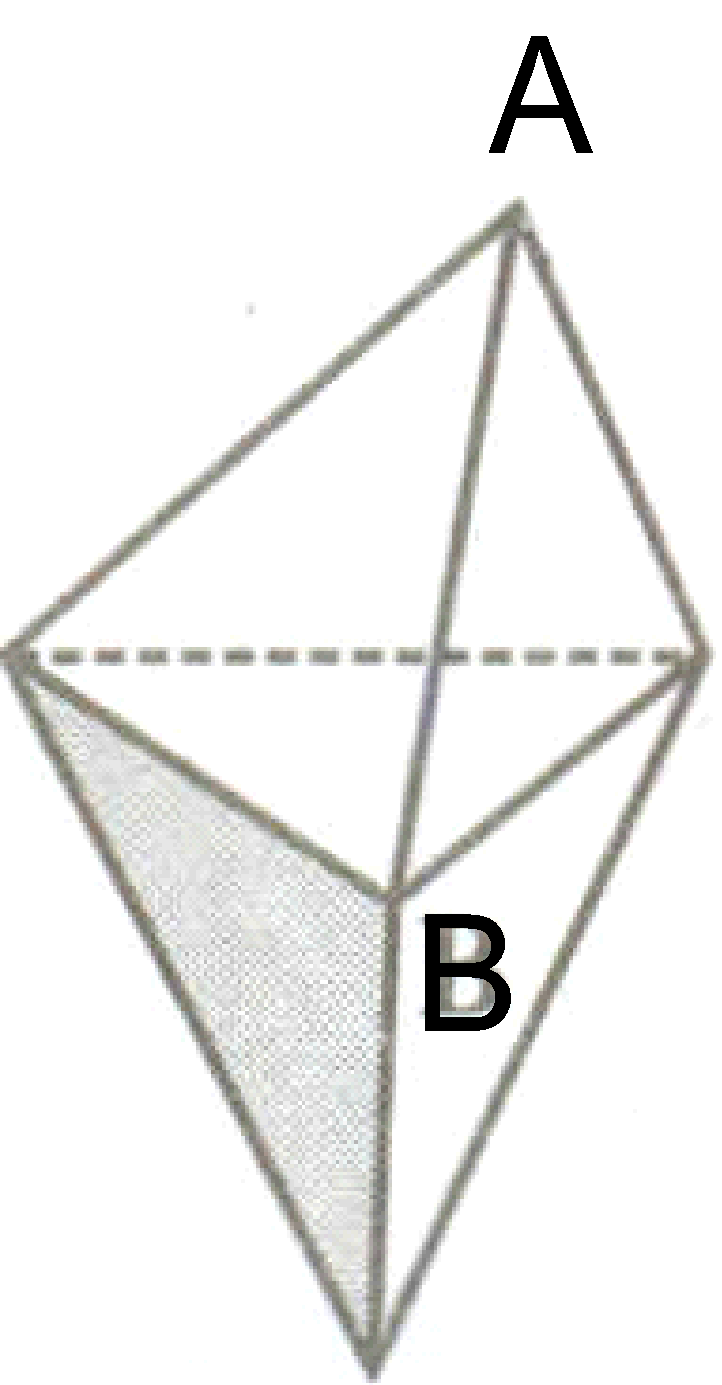
1. This polyhedron is regular. 2. Its faces are congruent, regular polygons. Vertices are formed by the same number of faces |
1. This polyhedron is not regular. 2. All the sides are congruent; but the vertices are not formed by the same number of faces. 3 faces meet at A but 4 faces meet at B. |
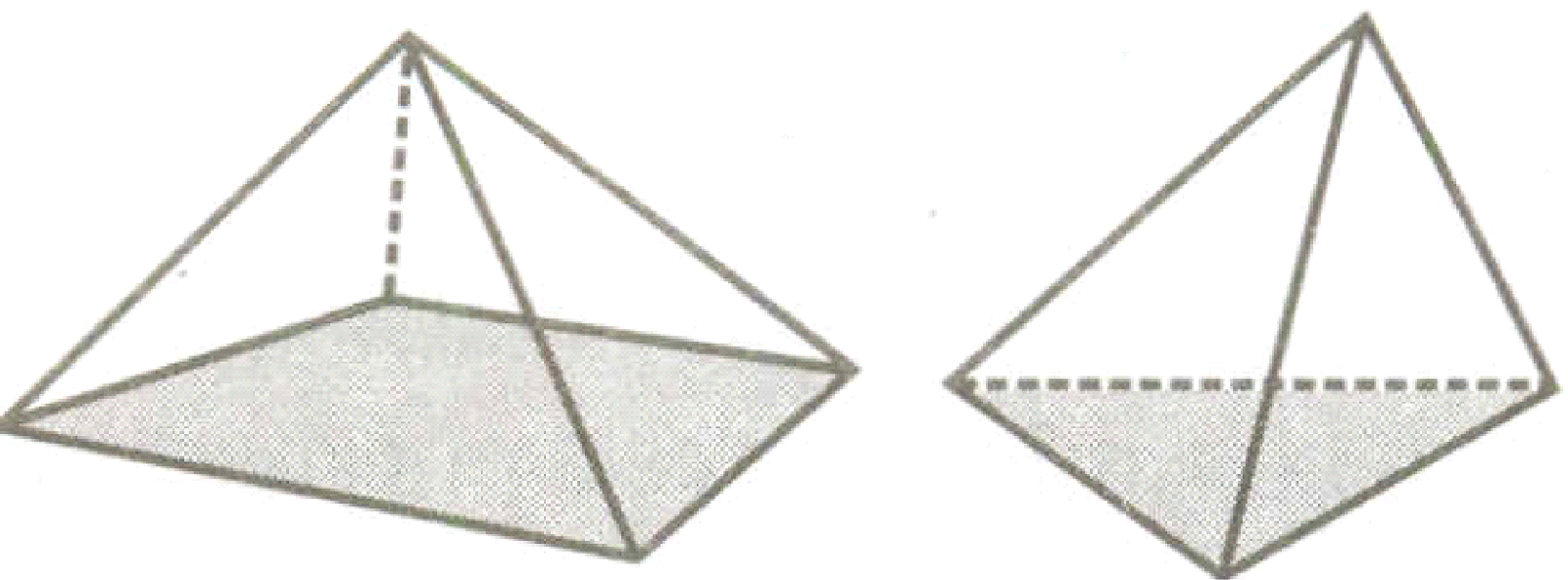
Two important members of polyhedron family around are prisms and pyramids.
|
These are prisms |
These are pyramids |
Prism
A solid whose two faces are parallel plane polygons and the side faces are rectangles is called a prism. A solid whose base and top are identical polygons and the sides are rectangles, is known as a prism. It is a polyhedron, two of whose faces are congruent polygons in parallel planes and whose other faces are parallelograms.
|
TYPES |
FIGURE |
FACES |
EDGES |
VERTICES |
|
|
(i) |
Triangular Prism |
|
5 |
9 |
6 |
|
(ii) |
Cuboid Rectangular Prism |
|
6 |
12 |
8 |
|
(iii) |
Square Prism |
|
6 |
12 |
8 |
|
(iv) |
Cube |
|
6 |
12 |
8 |
|
(v) |
Pentagonal Prism |
|
7 |
15 |
10 |
|
(vi) |
Cylinder |
|
3 |
2 |
– |
Pyramids
A pyramid is a polyhedron whose base is a polygon (of any number of sides) and whose other faces are triangles with a common vertex.
|
TYPES |
FIGURE |
FACES |
EDGES |
VERTICES |
|
|
(i) |
Triangular Pyramid |
|
4 |
6 |
4 |
|
(ii) |
Rectangular Pyramid |
|
5 |
8 |
5 |
|
(iii) |
Square Pyramid |
|
5 |
8 |
5 |
|
(iv) |
Pentagonal Pyramid |
|
6 |
10 |
6 |
- A prism is a polyhedron whose base and top are congruent polygons and whose other faces, i.e., lateral faces are parallelograms in shape.
- A pyramid is a polyhedron whose base is a polygon (of any number of sides) and whose lateral faces are triangles with a common vertex.
- A prism or a pyramid is named after its base. Thus a hexagonal prism has a hexagon as its base; and a triangular pyramid has a triangle as its base.
Any polyhedron can be built up from different kinds of element or entity, each associated with a different number of dimensions:
3 dimensions: The body is bounded by the faces, and is usually the volume enclosed by them.
2 dimensions: A face is a polygon bounded by a circuit of edges, and usually including the flat (plane) region inside the boundary. These polygonal faces together make up the polyhedral surface.
1 dimension: An edge joins one vertex to another and one face to another, and is usually a line segment. The edges together make up the polyhedral skeleton.
0 dimensions: A vertex (plural vertices) is a corner point.
-1 dimension: The null polytope is a kind of non-entity required by abstract theories.
EULER’S Formula
The table below shows the number of faces, edges and vertices of each of the platonic solids. Here, v stands for vertices, f for faces and e for edges.
|
Solid |
F |
V |
E |
F + V |
E + 2 |
|
Hexahedron (Cube) Octahedron Dodecahedron Icosohedron |
6 8 12 20 |
8 6 20 12 |
12 12 30 30 |
6 + 8 = 14 8 + 6 = 14 12 + 20 + 32 20 + 12 = 32 |
12 + 2 = 14 12 + 2 = 14 30 + 2 = 32 30 + 2 = 32 |
The above table clearly shows that
F + V = E + 2
Leonard Euler (1707-1783) discovered this formula which established the relationship among the number of faces, edges and vertices of a polyhedron.
Euler’s Formula
F + V = E + 2
Where F = number of faces
V = number of vertices
E = number of edges.
e.g. Try it on the cube:
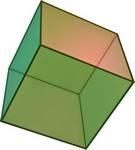
A cube has 6 Faces, 8 Vertices, and 12 Edges,
so: 6 + 8 - 12 = 2
EULER CHARACTERISTIC:
The Euler characteristic χ relates the number of vertices V, edges E, and faces F of a polyhedron:
x = V – E + F
For a convex polyhedron or more generally for any simply connected polyhedron whose faces are also simply connected and whose boundary is a manifold, χ = 2.
So, F+V-E can equal 2, or 1, and maybe other values, so the more general formula is
F + V - E = χ
Where χ is called the "Euler Characteristic".
Here are a few examples:
|
Shape |
|
χ |
|
Sphere |
|
2 |
|
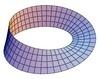
Torus |
|
0 |
|
Mobius Strip |
|
0 |
|
|
And the Euler Characteristic can also be less than zero. This is the "Cubohemioctahedron": It has 10 Faces (it may look like more, but some of the "inside" faces are really just one face), 24 Edges and 12 Vertices, so: F + V - E = -2 |
If any students need to take the online test to check their concepts or undertstanding then they can visit online test for class 8 maths .