Co-prime numbers formula consists of pairs of numbers that lack any shared factors except for 1. A co-prime set requires at least two numbers. These numbers share only 1 as their greatest common factor. For instance, examples of co-prime numbers are (4 and 7), and (5, 7, 9). It's important to recognize that co-prime numbers aren't exclusively prime; even composite numbers like 4 and 9 can create a co-prime pair.
What are Co-prime Numbers?
Two numbers, a and b, are considered co-prime if their only shared factor is 1. When the sole common divisor of a and b is 1, they form a co-prime pair, also known as a relatively prime pair.
Co-prime Number Definition
The definition of co-prime numbers states that when the Greatest Common Factor (GCF) of two numbers is 1, they are considered co-prime.
Co-prime Number List
Below is the list of a few co-primes for your reference.
|
Pairs of Co-prime Numbers
|
|
(2,15)
|
|
(3,8)
|
|
(4,9)
|
|
(5,6)
|
|
(11,14)
|
|
(15,19)
|
How to Find Co-prime Numbers?
To determine the co-primality of any two numbers, we start by calculating their Greatest Common Factor (GCF). If the GCF turns out to be 1, we can conclude that the numbers are co-prime.
For instance:
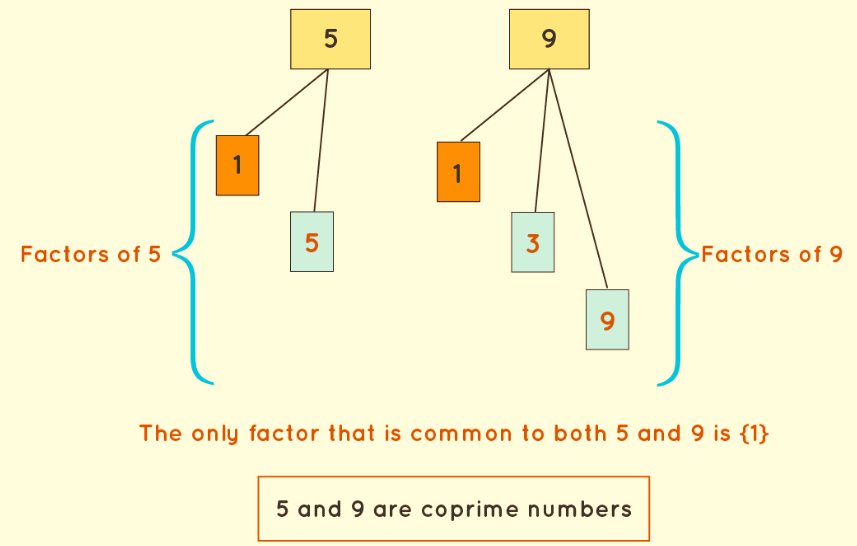
Example 1:
Consider the numbers 5 and 9. The factors of 5 are 1 and 5, while the factors of 9 are 1, 3, and 9. The sole factor common to both 5 and 9 is 1. Therefore, the GCF of (5, 9) is 1, indicating that (5, 9) constitutes a co-prime pair.
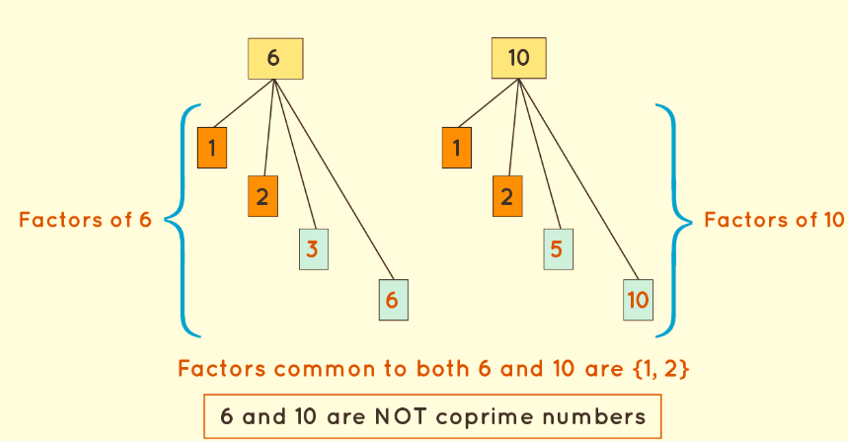
Example 2:
Take the numbers 6 and 10 as an illustration. The factors of 6 encompass 1, 2, 3, and 6, while the factors of 10 encompass 1, 2, 5, and 10. The shared factors between 6 and 10 are solely 1 and 2. Hence, the GCF of (6, 10) is calculated to be 2. As a result, it is evident that (6, 10) does not constitute a co-prime pair.
Also Check –
Line and Angles Formula
Properties of Co-prime Numbers Formula
Co-prime numbers can be easily identified using the following properties:
-
The Highest Common Factor (HCF) of two co-prime numbers is always 1. For instance, consider 5 and 9 as co-prime numbers; in this case, HCF(5, 9) = 1.
-
The Least Common Multiple (LCM) of two co-prime numbers is always their product. For example, take 5 and 9 as co-prime numbers, leading to LCM(5, 9) = 45.
-
The number 1 forms a co-prime pair with every other number.
-
Two even numbers cannot be co-prime since they always share 2 as a common factor.
-
The sum of two co-prime numbers is always co-prime with their product. As an illustration, consider co-prime numbers 5 and 9. In this case, 5 + 9 = 14 is co-prime with 5 × 9 = 45.
-
Two prime numbers are inherently co-prime. They only share 1 as a common factor. For example, take 29 and 31; both are prime numbers with no common factors except 1. Thus, they are co-prime. This holds true for other pairs of prime numbers like 2 and 3, 5 and 7, 11 and 13, and so on.
-
All pairs of consecutive numbers are co-prime. Any two consecutive numbers share 1 as their only common factor.
Consider a few pairs of such numbers. Let us try with 14 and 15.
|
Numbers
|
14
|
15
|
|
Factors
|
1,2,7,14
|
1,3,5,15
|
|
Common Factor
|
1
|
|
There are multiple such combinations where 1 is the only common factor.
Co-prime and Twin Prime Numbers
Co-prime numbers are defined by having a Highest Common Factor (HCF) of 1. In contrast, twin prime numbers are prime numbers with a consistent difference of 2. For instance, 3 and 5 are twin prime numbers. Here's a breakdown of the distinctions between co-prime and twin-prime numbers:
-
Twin prime numbers are always prime, whereas co-prime numbers can include both prime and composite numbers.
-
The gap between two twin primes is invariably 2, whereas the gap between two co-primes can vary.
-
Every pair of twin prime numbers is inherently co-prime, but not all co-prime numbers qualify as twin primes.
-
The number 1 forms a co-prime pair with any number, whereas it exclusively forms a twin prime pair with 3
Also Check –
Introduction to Graph Formula
Co-prime Numbers 1 to 100
In the range of numbers from 1 to 100, numerous pairs can be identified as co-prime based on the aforementioned properties. A selection of co-prime number pairs existing between 1 and 100 includes (1, 2), (3, 67), (2, 7), (99, 100), (34, 79), (54, 67), (10, 11), and more. Feel free to explore additional sets of co-prime number pairs within this range.
Important Notes
Co-prime numbers are defined by having a Greatest Common Factor (GCF) of 1. This means that if the GCF of any two numbers is 1, those numbers are considered co-prime.
It's important to note that co-prime numbers do not have to be prime numbers themselves. For instance, the numbers 12 and 35 are co-prime, even though neither of them is a prime number.
Tips and Tricks
-
Any two prime numbers are always co-prime.
-
Any two consecutive numbers are always co-prime.
-
The number 1 forms a co-prime pair with any other number.
-
A prime number is co-prime with any number that is not a multiple of it.
-
Two even numbers are never co-prime due to their common factor of 2.
Also Check –
Solid Shapes Formula
Co-Prime Numbers Formula Examples
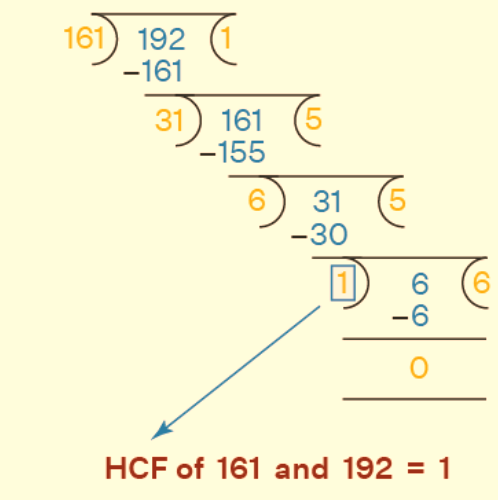
Example 1:
Demonstrate that 161 and 192 are co-prime numbers.
Solution:
To establish this, we'll determine the Highest Common Factor (HCF) of the provided numbers 161 and 192 using the division method.
Example 2:
If 59 and 97 are co-prime, what is their Highest Common Factor (HCF)?
Solution:
Given that 59 and 97 are co-prime, they do not share any common factors except for 1. Consequently, their Highest Common Factor (HCF) is 1.
Example 3:
Determine the accuracy of the following statements regarding co-prime numbers.
a.) Co-prime numbers need not necessarily be prime numbers.
b.) Two even numbers are always co-prime.
Solution:
a.) True. Co-prime numbers can include both prime and composite numbers.
b.) False. Two even numbers are never co-prime due to their shared factor of 2.
