Solid Shapes Formula: Solid shapes are essentially three-dimensional objects, characterized by their measurements in length, breadth, and height. These shapes are commonly referred to as 3D shapes. Unlike two-dimensional shapes, solid shapes possess volume and are encountered in our daily experiences. We interact with them physically, sensing their presence.
What are Solid Shapes?
Within the realm of mathematics, our focus is directed toward the examination of various shapes and their diverse classifications, seeking practical applications in the real world. Our current pursuit involves a comprehensive exploration of each distinct solid shape. These solid shapes are categorized into multiple groups, with certain shapes boasting curved surfaces while others exhibit characteristics reminiscent of pyramids or prisms.
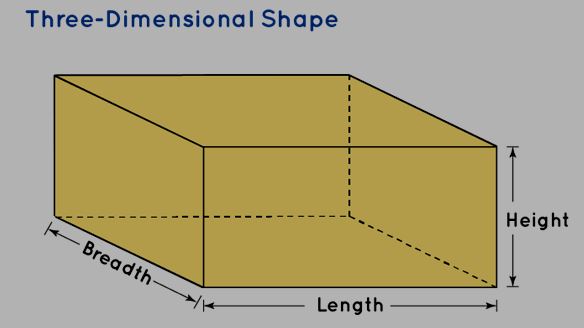
Solid Shapes:
These are three-dimensional entities that possess three defining dimensions—length, breadth, and height.
Three-Dimensional Forms
: To begin our exploration, we will delve into solid shapes that exhibit curved surfaces, and we will illustrate this with accompanying examples.
Download PDF Solid Shapes
Also Read -
Ratio and Proportion Formula
Solid Shapes and Their Properties
Solid shapes pertain to objects existing in three dimensions. Just take a moment to observe your surroundings. Everyday items like laptops, cellphones, ice-cream cones, and balls are all instances of solid shapes. These objects occupy a physical space and possess measurements in terms of length, width, and height. Let's delve into the various categories of solid shapes:
-
Sphere
-
Cylinder
-
Cone
-
Pyramid
-
Prism
Sphere
A sphere represents a solid shape that is perfectly round in three-dimensional space. Every point on its surface is equidistant from the center.
|
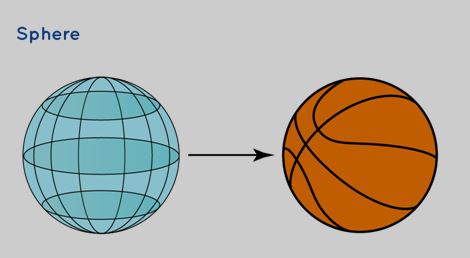
Properties
|
Surface Area
|
Volume
|
-
There are no edges or vertices (corners) on it.
-
It possesses a singular surface.
-
Its configuration resembles that of a ball and demonstrates impeccable symmetry.
-
The distance (r) from the center to any point on its surface remains consistent.
|
4πr
2
|
(4/3)πr
3
|
Also Read -
Line and Angles Formula
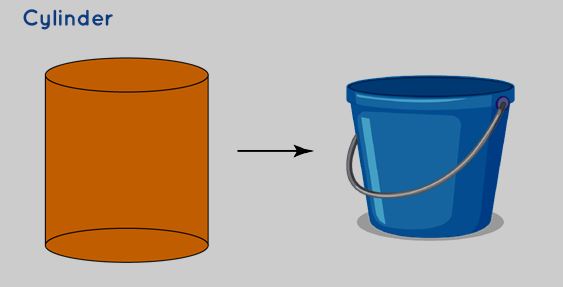
Cylinder
A cylinder is a three-dimensional solid shape characterized by its structure. It consists of two parallel circular bases connected by a curved surface, resembling a tube. The bases and the connecting surface are fixed at a consistent distance from each other.
|
Properties
|
Surface Area
|
Volume
|
|
• Its structure includes a flat bottom and a flat upper surface.
• The shape exhibits a single curved side.
• The bases are invariably both congruent and parallel.
• This three-dimensional object features two identical ends, which can either be circular or oval in shape.
|
2πr (r+h)
|
πr
2
h
|
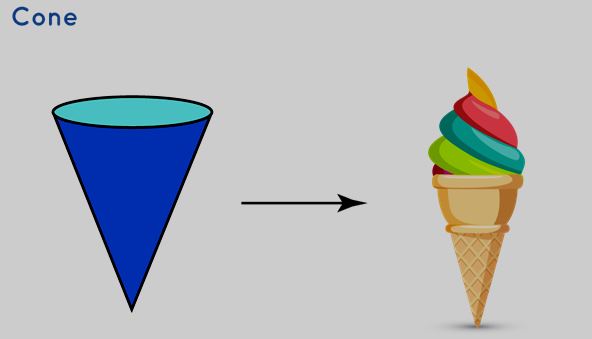
Cone
A cone stands as a unique three-dimensional solid shape within the realm of geometry. It encompasses both a flat surface and a curved surface, with the latter extending towards the uppermost point. Its formation is accomplished by connecting a series of line segments that stretch from the circular base to a shared point called the apex or vertex. Depending on the alignment of the apex in relation to the center of the base, the cone can either be categorized as a right cone or an oblique cone.
|
Properties
|
Surface Area
|
Volume
|
-
The base of the cone is either circular or oval, while an apex (or vertex) crowns it.
-
The shape is characterized by a solitary curved side.
-
A cone can be visualized as a triangle that has been rotated.
|
π r(r + s)
|
1/3 πr
2
h
|
Pyramid
A pyramid constitutes a solid shape or a polyhedron featuring a base formed by a polygon, with its lateral faces comprising exclusively of triangles. These pyramids are generally characterized by the geometry of their bases. Specifically, a pyramid with:
-
A triangular base is referred to as a Tetrahedron.
-
A quadrilateral base is recognized as a square pyramid.
-
A pentagon base is designated as a pentagonal pyramid.
-
A base in the shape of a regular hexagon is identified as a hexagonal pyramid.
|
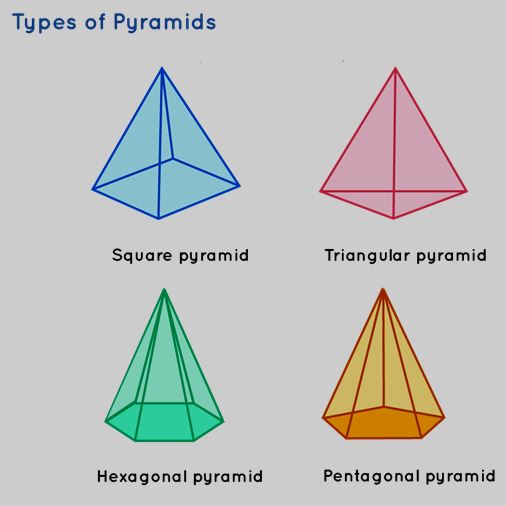
Properties
|
Surface Area
|
Volume
|
-
A pyramid represents a polyhedron featuring a polygonal base and a vertex connected by straight lines.
-
They can be categorized as regular or oblique pyramids depending on how their vertex aligns with the center of the base.
|
BA + 1/2 × P × (SH)
|
1/3 BA
2
|
Prisms
A prism is a three-dimensional solid shape characterized by two identical shapes placed face to face. Various types of prisms include triangular prisms, square prisms, pentagonal prisms, hexagonal prisms, and so on. Prisms can also be broadly categorized as regular prisms and oblique prisms.
Varieties of Prisms
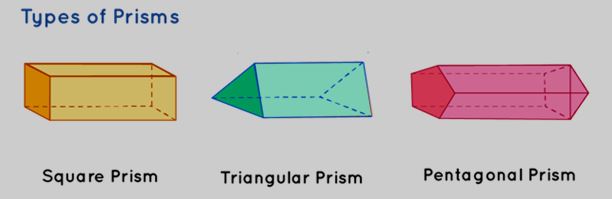
The following table provides information about the properties of a prism: (BA = base area, P = perimeter, H = height)
|
Properties
|
Surface Area
|
Volume
|
-
It possesses uniform polygonal ends and flat surfaces.
-
Its cross-sectional shape remains consistent throughout its entire length
.
|
2 × (BA) + P × H
|
BA × H
|
Also Read -
Introduction to Graph Formula
Polyhedrons/Platonic Solids
Platonic solids exhibit faces that are identical to regular polygons. There exist five distinct polyhedra within this category:
Tetrahedron:
Featuring four equilateral triangular faces.
Octahedron:
Comprising eight equilateral triangular faces.
Dodecahedron:
Possessing twelve pentagonal faces.
Icosahedron:
Displaying twenty equilateral triangular faces.
Hexahedron or cube:
Characterized by six square faces.
|
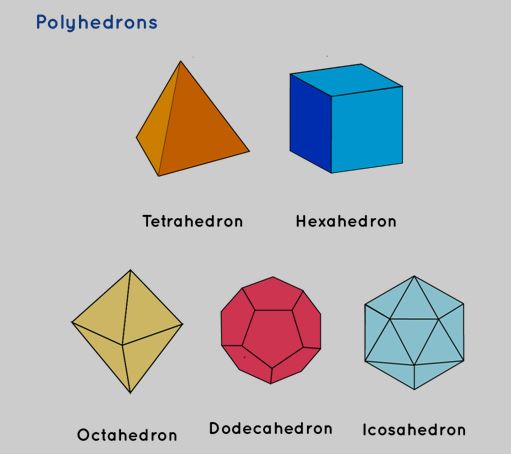
Properties of Cube
|
Surface Area
|
Volume
|
-
With 6 faces, each forming a square shape.
-
A total of 12 edges define its structure.
-
It boasts 8 vertices, where 3 edges converge at each corner.
|
6 × (EL)
2
|
(EL)
3
|
Also Read -
Factorization Formula
As previously mentioned, three-dimensional objects and entities distinguish themselves from two-dimensional counterparts due to the incorporation of three dimensions: length, width, and height. This introduction of three dimensions bestows these objects with facets, borders, and corners. Let's delve into a comprehensive understanding of these three aspects.
Faces, Edges, and Vertices of Solid Shapes
Faces of Solid Shapes
-
A face refers to any single flat surface of a solid object.
-
Solid shapes can have more than one face.
Edges of Solid Shapes
-
An edge is a line segment on the boundary joining one vertex (corner point) to another.
-
They serve as the junction of two faces.
Vertices of Solid Shapes
-
A point where two or more lines meet is called a vertex.
-
It is a corner.
-
The point of intersection of edges denotes the vertices.
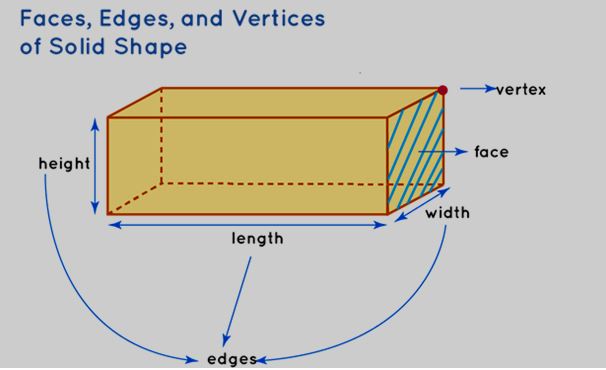
Important Points
-
Three-dimensional objects, commonly referred to as solids, possess three essential dimensions: length, breadth, and height.
-
Solid shapes exhibit distinct features in the form of faces, edges, and vertices.
-
Gaining knowledge about these solid shapes holds practical value for our daily routines, as a significant portion of our activities and dependencies is centered around them.
