Continuity and Differentiability Formula: Definition, Explanation, and Solved Examples
Continuity and differentiability formula are fundamental concepts in calculus that describe the behavior of a function. These concepts are interrelated, but they have distinct definitions and criteria.
Anchal Singh14 Sept, 2023
Share
Continuity and differentiability formula are fundamental concepts in calculus that describe the behavior of a function. These concepts are interrelated, but they have distinct definitions and criteria.
Continuity:
A function y=f(x) is said to be continuous at a point x=c if the limit of the function as x approaches c exists and is equal to the value of the function at x=c. Mathematically, this is expressed as: lim[x → c] f(x) = f(c). In simple terms, for a function to be continuous at a point c, there should be no jumps, holes, or asymptotes in the graph of the function at that point. The graph is a single, connected curve.Differentiability:
A function y=f(x) is said to be differentiable at a point x=c if the limit of the derivative of the function as x approaches c exists and is equal to the instantaneous rate of change (slope) of the function at x=c. Mathematically, this is expressed as: f'(c) = lim[x → c] (f(c + h) - f(c)) / h. In simpler terms, a function is differentiable at a point if it has a well-defined tangent line at that point. The tangent line represents the instantaneous rate of change of the function.Also Check - solid shapes Formula
Relationship:
While continuity is a necessary condition for differentiability, it is not a sufficient condition. In other words, if a function is differentiable at a point, it must also be continuous at that point, but the reverse is not necessarily true.To be differentiable, a function not only needs to be continuous but also must have a well-defined slope (derivative) at that point.Continuity Of A Function
Continuity, in the context of a graph represented by y = f(x), can be straightforwardly described as the ability to sketch the graph seamlessly, without the need to lift the pencil at any point. Let's consider a real-valued function, f(x), defined on a subset of real numbers, and let's suppose c is a point within the domain of the function f(x). We assert that the function f(x) is continuous at the point x = c if the limit as x approaches c of f(x) equals the value of f(c), expressed as: lim[x → c] f(x) = f(c).Also Check - Introduction to Euclid Formula
The concept of continuity for a function can be elucidated through graphical or algebraic means. In a graph, the continuity of a function represented as y = f(x) at a particular point is visually depicted by a smooth, uninterrupted curve passing through that point, devoid of any abrupt breaks or discontinuities.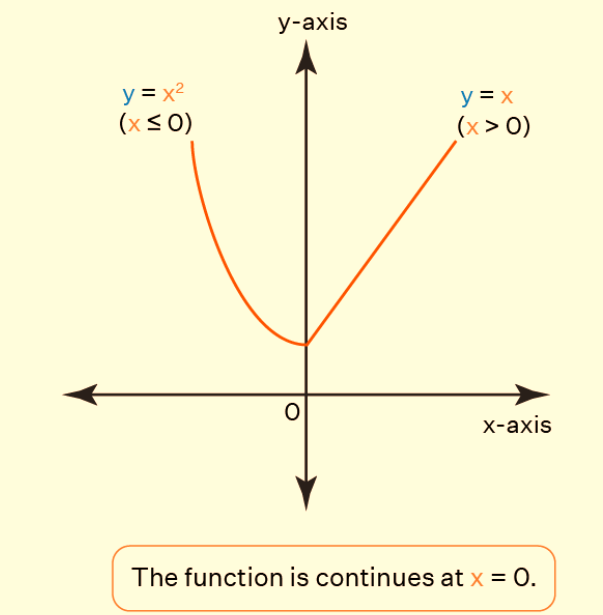
Algebraically, the continuity of a function y = f(x) can be ascertained by verifying whether the value of the function from the left-hand limit is equal to the value of the function from the right-hand limit:
lim[x → 1-] f(x) = lim[x → 1+] f(x).
This means that for values of x slightly less than 1 (e.g., 0.99, 0.998) and values slightly greater than 1 (e.g., 1.001, 1.0001), the function f(x) retains the same value as it does at x = 1. In other words, there is no abrupt jump or discontinuity in the function at x = 1, ensuring its continuity.
Differentiability Of A Function
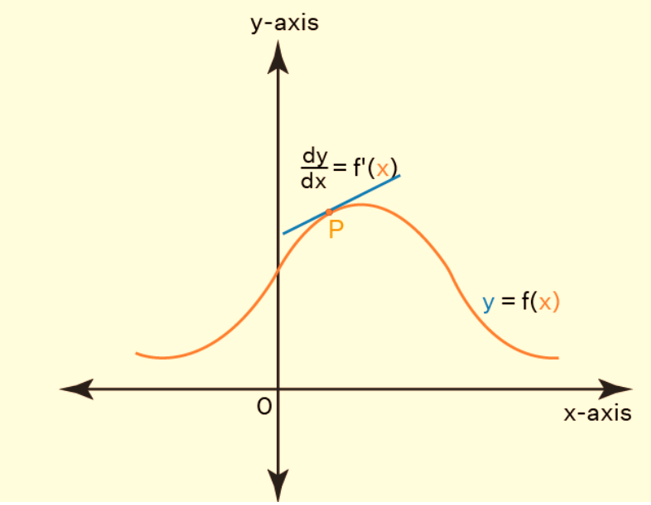
Differentiation of a function provides insight into how the function's value changes concerning variations in its domain. Understanding the differentiability of a function can be approached from both graphical and algebraic perspectives. From a geometric standpoint, differentiating a function corresponds to determining the slope of the graph of the function, denoted as y = f(x), at a specific point, typically denoted as x = a, within the function's domain.
Also Check - Polynomials formula
This process of finding the derivative is referred to as differentiation. Additionally, the phrase "differentiate f(x) with respect to x" is used to indicate dy/dx or f'(x). There are three fundamental rules governing the algebra of differentiation for functions: (f + g)'(x) = f'(x) + g'(x) (f * g)'(x) = f'(x) * g(x) + g'(x) * f(x) (f / g)'(x) = (f'(x) * g(x) - g'(x) * f(x)) / (f(x))^2 Furthermore, there are specific differentiation rules for various types of functions, including:- Derivative of Composite Functions
- Derivatives of Implicit Functions
- Derivatives of Inverse Trigonometric Functions
- Derivatives of Exponential Functions
- Derivatives of Logarithmic Functions
- Derivatives of Functions in Parametric Forms
Theorems on Continuity And Differentiability Formula
Theorem 1: If two functions, f(x) and g(x), are both continuous at a real-valued function and continuous at a point x = c, the following hold: f(x) + g(x) is continuous at the point x = c. f(x) - g(x) is continuous at the point x = c. g(x) * g(x) is continuous at the point x = c. f(x)/g(x) is continuous at the point x = c, provided that g(c) ≠ 0. Theorem 2: For two real-valued functions, f(x) and g(x), such that the composite function f∘g(x) is defined at x = c, if g(x) is continuous at x = c and f(x) is continuous at g(c), then f∘g(x) is continuous at x = c. Theorem 3: If a given function f(x) is differentiable at a point x = c, then it is continuous at that point. In summary, every differentiable function is continuous. Theorem 4 (Chain Rule): For a real-valued function f(x), which is a composite of two functions u and v, i.e., f = v∘u. Also, let t = u(x), and if both dt/dx and dv/dt exist, then df/dx = dv/dt * dt/dx. Theorem 5: The derivative of e^x with respect to x is e^x, expressed as d/dx(e^x) = e^x. The derivative of ln(x) with respect to x is 1/x, written as d/dx(ln(x)) = 1/x. Theorem 6 (Rolle's Theorem): If a function f(x) is continuous across the closed interval [a, b] and differentiable across the open interval (a, b), and if f(a) = f(b), where a and b are real numbers, then there exists a point c in the open interval (a, b) such that f'(c) = 0. Theorem 7 (Mean Value Theorem): If a function f(x) is continuous across the closed interval [a, b] and differentiable across the open interval (a, b), then there exists a point c in the open interval (a, b) such that f'(c) is equal to the average rate of change of f(x) over the interval [a, b]. This is expressed as f'(c) = (f(b) - f(a)) / (b - a).Examples on Continuity And Differentiability Formula
Example 1: Determine the continuity of the function f(x) = 3x + 4 at the point x = 5. Solution: We are given the function f(x) = 3x + 4, and we want to assess its continuity at x = 5. Let's calculate the limit of the function as x approaches 5: lim[x → 5] f(x) = lim[x → 5] (3x + 4) = 3 * 5 + 4 = 15 + 4 = 19. Since the limit of the function as x approaches 5 equals the value of the function at x = 5, i.e., lim[x → 5] f(x) = f(5), we can conclude that the function f(x) is continuous at the point x = 5. Example 2: Find the derivative of the function f(x) = arctan(x). Solution: The given function is f(x) = arctan(x), which can also be expressed as y = arctan(x). y = arctan(x) x = tan(y) Now, let's differentiate both sides with respect to x: d/dx(x) = d/dx(tan(y)) 1 = sec²(y) * dy/dx dy/dx = 1/sec²(y) dy/dx = 1/(1 + tan²(x)) dy/dx = 1/(1 + tan²(arctan(x))) dy/dx = 1/(1 + x²) Therefore, the derivative of the function arctan(x) is 1/(1 + x²).Continuity and Differentiability Formula FAQs
Define the term Continuity.
A function y=f(x) is said to be continuous at a point x=c if the limit of the function as x approaches c exists and is equal to the value of the function at x=c. Mathematically, this is expressed as
Define the term Differentiability.
A function y=f(x) is said to be differentiable at a point x=c if the limit of the derivative of the function as x approaches c exists and is equal to the instantaneous rate of change (slope) of the function at x=c. Mathematically, this is expressed as
State some of the uses of Continuity and Differentiability Formula.
The uses of Continuity and Differentiability Formula. calculation of maxima and minima, tangent and normal, rate of change etc.
State true or false: Every differentiable function is Continuous.
True
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App