Cyclic Quadrilateral Formula: Properties, Angles

A cyclic quadrilateral is a type of quadrilateral whose four vertices lie on the circumference of a circle. This means that you can draw a circle that passes through all four vertices of the quadrilateral. Cyclic quadrilaterals are also known as inscribed quadrilaterals. To understand the better picture of cyclic quadrilateral formula we will be starting with the key points.

Key properties of cyclic Quadrilaterals Include:

Opposite Angles Sum to 180 Degrees: In a cyclic quadrilateral, the sum of the measures of the opposite angles is always equal to 180 degrees. This property is a consequence of the fact that the opposite sides of the quadrilateral subtend arcs on the circle whose sum is 360 degrees.

Diagonals Intersect on the Circle: The diagonals of a cyclic quadrilateral intersect at a point that lies on the circumcircle (the circle passing through all four vertices). This point is called the "circumcenter."

Angle Bisectors: The lines connecting the vertices of the cyclic quadrilateral to the circumcenter are angle bisectors of the opposite angles of the quadrilateral.

Area Formula: If you know the side lengths of a cyclic quadrilateral and its diagonals, you can use the Brahmagupta formula to calculate its area.

Cyclic quadrilaterals have various applications in geometry and trigonometry, and they are used to solve problems involving angles, side lengths, and area calculations in geometric problems.

Cyclic Quadrilateral Definition

A cyclic quadrilateral is a type of quadrilateral defined by a specific geometric property. It is a four-sided polygon in which all four vertices (corners) of the quadrilateral lie on the circumference of a circle. In other words, you can draw a circle that passes through all four vertices of the quadrilateral, making the circle circumscribe the quadrilateral.

The term "cyclic" in "cyclic quadrilateral" refers to the circular or circular-like arrangement of its vertices. This characteristic sets cyclic quadrilaterals apart from other quadrilaterals whose vertices do not necessarily fall on a common circle.

Cyclic Quadrilateral Angles

Cyclic quadrilaterals exhibit specific angle properties that are important to understand. Here are the key angle-related properties of cyclic quadrilaterals:

Sum of Opposite Angles is Supplementary:

In a cyclic quadrilateral, the sum of the measures of opposite angles is always supplementary, meaning they add up to 180 degrees.

For a cyclic quadrilateral ABCD, this property can be expressed as follows:

∠A + ∠C = 180 degrees

∠B + ∠D = 180 degrees

Angle Sum Property:

In addition to the property mentioned above, cyclic quadrilaterals also follow the general angle sum property of quadrilaterals. The sum of all the angles in a quadrilateral, including cyclic quadrilaterals, equals 360 degrees.

For a cyclic quadrilateral ABCD, this property can be expressed as follows:

∠A + ∠B + ∠C + ∠D = 360 degrees

Special Relationships Between Certain Angles:

In a cyclic quadrilateral, angles that are opposite to each other are congruent. This means that ∠A is congruent to ∠C, and ∠B is congruent to ∠D.

These angle properties are fundamental to working with cyclic quadrilaterals and can be used to solve various geometric problems involving angles and side lengths within such quadrilaterals.

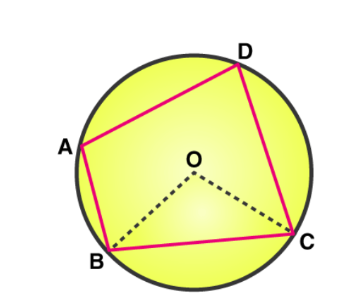
Radius of Cyclic Quadrilateral

The radius of a cyclic quadrilateral is a measure used to describe certain properties of the quadrilateral in relation to the circle within which it is inscribed. To clarify, here's the formula for calculating the radius of a cyclic quadrilateral:

If a, b, c, and d are the consecutive side lengths of a cyclic quadrilateral, and s is the semiperimeter (half the sum of the side lengths), then the radius (R) can be calculated using the following formula:

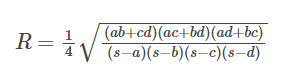
Diagonals of Cyclic Quadrilaterals

Intersection on the Circumcircle:

The diagonals of a cyclic quadrilateral intersect at a point that lies on the circumcircle of the quadrilateral. This point of intersection is known as the "circumcenter" of the cyclic quadrilateral.

The circumcenter is equidistant from all four vertices of the cyclic quadrilateral because it is the center of the circle that passes through those vertices.

Perpendicular Bisectors:

The line segments connecting the circumcenter to the vertices of the cyclic quadrilateral are the perpendicular bisectors of the sides of the quadrilateral.

These perpendicular bisectors divide the diagonals of the cyclic quadrilateral into two equal parts.

Equal Products of Diagonals:

Suppose a, b, c, and d are the sides of the cyclic quadrilateral, and p and q are the diagonals. Then, you can find the products of the diagonals using the following formulas:

pq = ac + bd

pq = ad + bc

These properties of the diagonals in a cyclic quadrilateral are essential for understanding its geometry and can be used to derive various theorems and solve geometric problems involving such quadrilaterals.

Area of Cyclic Quadrilateral

The area of a cyclic quadrilateral can be calculated using the following formula:

Area (A) = √[s(s - a)(s - b)(s - c)(s - d)]

Where:

A is the area of the cyclic quadrilateral.

a, b, c, and d are the lengths of its consecutive sides.

s is the semiperimeter, calculated as s = ½(a + b + c + d).

This formula allows you to find the area of a cyclic quadrilateral when you know the lengths of its sides. It's a useful tool for solving geometric problems involving such quadrilaterals.

Cyclic Quadrilateral Theorems

Theorem 1:

In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.

Proof:

Let's consider a cyclic quadrilateral ABCD inscribed in a circle with center O.

Draw lines connecting the opposite vertices:

Join A and C with center O.

Since each of these lines passes through the center of the circle, they are radii of the same circle.

The measure of an angle subtended by an arc at the center of a circle is twice the measure of the angle subtended by the same arc at the circumference. Therefore, ∠AOC = 2∠ABC and ∠COD = 2∠CDA.

The sum of angles around a point is 360 degrees. So, ∠AOC + ∠COD = 360 degrees.

Substituting the angles we found, 2∠ABC + 2∠CDA = 360 degrees.

Dividing both sides by 2, we get ∠ABC + ∠CDA = 180 degrees.

This proves that in a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.

Theorem 2 (Cyclic Quadrilateral Theorem):

The product of the diagonals of a cyclic quadrilateral is equal to the sum of the products of its two pairs of opposite sides.

Proof:

Let PQRS be a cyclic quadrilateral with diagonals PR and QS intersecting at point X. Also, let the lengths of its sides be a, b, c, and d, with a and c being opposite to each other and b and d being opposite to each other.

By Theorem 1, we know that ∠QPS + ∠QRS = 180 degrees and ∠PQS + ∠PRS = 180 degrees.

Consider the triangles PXQ and SXQ.

In triangle PXQ, by the Angle Sum Property, ∠PXS + ∠QXS + ∠PXQ = 180 degrees.

In triangle SXQ, by the Angle Sum Property, ∠QXS + ∠SXS + ∠SXQ = 180 degrees.

Subtract the common angle ∠QXS from both equations:

∠PXS + ∠PXQ = 180 degrees

∠SXS + ∠SXQ = 180 degrees

Add these two equations together:

(∠PXS + ∠PXQ) + (∠SXS + ∠SXQ) = 180 degrees + 180 degrees

2(∠PXS + ∠PXQ) = 360 degrees

Divide both sides by 2:

∠PXS + ∠PXQ = 180 degrees

But ∠PXS + ∠PXQ = ∠QPS + ∠QRS (because they subtend the same arc QS).

So, ∠QPS + ∠QRS = 180 degrees.

Using the same logic, we can prove that ∠PQS + ∠PRS = 180 degrees.

Now, consider the triangles PXQ and RXS.

By the Angle Sum Property in triangle PXQ, we have ∠PXS + ∠PXQ + ∠QPS = 180 degrees.

By the Angle Sum Property in triangle RXS, we have ∠QXS + ∠SXS + ∠PRS = 180 degrees.

Subtract the common angles ∠PXS and ∠QXS from both equations:

∠PXQ + ∠QPS = 180 degrees

∠SXS + ∠PRS = 180 degrees

Add these two equations together:

(∠PXQ + ∠QPS) + (∠SXS + ∠PRS) = 180 degrees + 180 degrees

2(∠PXQ + ∠QPS) = 360 degrees

Divide both sides by 2:

∠PXQ + ∠QPS = 180 degrees

But ∠PXQ + ∠QPS = ∠PQS + ∠PRS (because they subtend the same arc PQ).

So, ∠PQS + ∠PRS = 180 degrees.

Now, consider the triangles PXQ and RXS.

By the Angle Sum Property in triangle PXQ, we have ∠QXS + ∠PXQ + ∠QPS = 180 degrees.

By the Angle Sum Property in triangle RXS, we have ∠PXS + ∠SXS + ∠PRS = 180 degrees.

Subtract the common angles ∠PXS and ∠QXS from both equations:

∠PXQ + ∠QPS = 180 degrees

∠SXS + ∠PRS = 180 degrees

Add these two equations together:

(∠PXQ + ∠QPS) + (∠SXS + ∠PRS) = 180 degrees + 180 degrees

2(∠PXQ + ∠QPS) = 360 degrees

Divide both sides by 2:

∠PXQ + ∠QPS = 180 degrees

∠PXQ + ∠QPS = ∠PQS + ∠QRS (because they subtend the same arc QR).

So, ∠PQS + ∠QRS = 180 degrees.

Now, consider the triangles PXQ and RXS.

By the Angle Sum Property in triangle PXQ, we have ∠PXS + ∠PXQ + ∠QPS = 180 degrees.

By the Angle Sum Property in triangle RXS, we have ∠SXS + ∠RXQ + ∠QRS = 180 degrees.

Subtract the common angles ∠PXQ and ∠RXQ from both equations:

∠PXS + ∠QPS = 180 degrees

∠SXS + ∠QRS = 180 degrees

Add these two equations together:

(∠PXS + ∠QPS) + (∠SXS + ∠QRS) = 180 degrees + 180 degrees

2(∠PXS + ∠QPS) = 360 degrees

Divide both sides by 2:

∠PXS + ∠QPS = 180 degrees

But ∠PXS + ∠QPS = ∠PQS + ∠QRS (because they subtend the same arc PS).

So, ∠PQS + ∠QRS = 180 degrees.

This completes the proof of the theorem.

These theorems related to cyclic quadrilaterals are essential in geometry and are used to solve various problems involving such quadrilaterals.

Properties of Cyclic Quadrilateral Formula

Sum of Opposite Angles is Supplementary:

In a cyclic quadrilateral, the sum of the measures of opposite angles is always 180 degrees. This is because the opposite sides of the cyclic quadrilateral subtend arcs on the circle whose total measure is 360 degrees.

Diagonals Intersect on the Circumcircle:

The diagonals of a cyclic quadrilateral intersect at a point that lies on the circumcircle, which is the circle passing through all four vertices of the quadrilateral. This point is known as the "circumcenter" of the cyclic quadrilateral.

The circumcenter is equidistant from all four vertices of the cyclic quadrilateral.

Angle Bisectors:

The lines drawn from the vertices of the cyclic quadrilateral to the circumcenter are angle bisectors of the opposite angles of the quadrilateral.

These angle bisectors divide the opposite angles into two congruent angles.

Equal Products of Diagonals:

If a, b, c, and d are the consecutive side lengths of a cyclic quadrilateral, and p and q are the diagonals, then you can find the products of the diagonals using the following formulas:

pq = ac + bd

pq = ad + bc

Area Formula:

The area of a cyclic quadrilateral can be calculated using Brahmagupta's formula:

Area (A) = √[(s - a)(s - b)(s - c)(s - d)]

Where s is the semiperimeter, and a, b, c, and d are the consecutive side lengths of the cyclic quadrilateral.

Midpoint Connection:

Joining the midpoints of the four sides of a cyclic quadrilateral results in a rectangle or parallelogram.

Exterior Angle Property:

The exterior angle formed when any one side of the cyclic quadrilateral is extended is equal to the interior angle opposite to it.

Perpendicular Bisectors:

In a cyclic quadrilateral, the perpendicular bisectors of the four sides are concurrent, meaning they intersect at a single point.

These properties are fundamental in understanding and working with cyclic quadrilaterals in geometry and are used to derive various theorems and solve geometric problems involving such quadrilaterals.

Problems and Solutions

Problem 1:

Find the measure of angle D in a cyclic quadrilateral ABCD, given that angle B measures 60 degrees.

Solution:

In a cyclic quadrilateral like ABCD, the sum of a pair of opposite angles is always 180 degrees.

So, ∠B + ∠D = 180 degrees.

Given that ∠B = 60 degrees:

60 degrees + ∠D = 180 degrees

Now, solve for ∠D:

∠D = 180 degrees - 60 degrees

∠D = 120 degrees

Therefore, the measure of angle D is 120 degrees.

Problem 2:

Determine the measure of angle D in a cyclic quadrilateral ABCD, when angle B has a measure of 80 degrees.

Solution:

In a cyclic quadrilateral such as ABCD, the sum of opposite angles is always 180 degrees.

So, ∠B + ∠D = 180 degrees.

Given that ∠B = 80 degrees:

80 degrees + ∠D = 180 degrees

Now, find the value of ∠D:

∠D = 180 degrees - 80 degrees

∠D = 100 degrees

Hence, the measure of angle D is 100 degrees.

To gain a better understanding of this concept, it is recommended to practice more examples using the properties of cyclic quadrilaterals.