
Difference Quotient Formula is a mathematical formula used in calculus to approximate the derivative of a function at a specific point. It provides an approximation of the slope of the tangent line to the curve of the function at that point.
The difference quotient formula plays a fundamental role in defining the derivative of a function. It involves taking the limit as a small increment, denoted as "h," tends to zero to calculate the derivative of the function at a specific point. Let's delve into the difference quotient formula, its derivation, and explore illustrative examples to gain a deeper understanding of this concept.
Difference Quotient Formula Definition
The term "difference quotient formula" does suggest a connection to finding slopes, and it indeed relates to the slope of a secant line on a curve. A secant line is a straight line that intersects a curve at two distinct points. In the context of a function f(x), if we choose two points (x,f(x)) and (x+h,f(x+h)) on the curve, we can calculate the slope of the secant line connecting these points. This calculation is precisely what the difference quotient formula accomplishes.
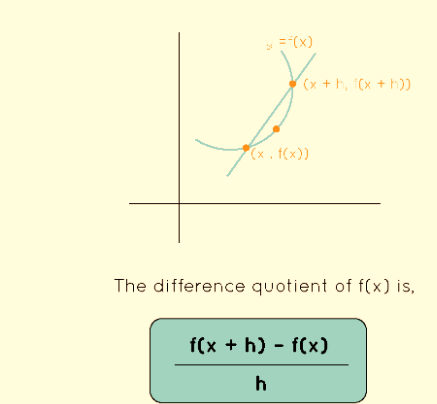
The difference quotient formula allows us to estimate the slope of this secant line, and as we let the "h" value approach zero, it helps us determine the slope of the tangent line, which is the derivative of the function at a specific point. This process is integral to understanding the concept of the derivative in calculus and is a key step in analyzing the behavior of functions. If you have any specific questions or would like to explore examples further, please feel free to ask.
Difference Quotient Formula
The difference quotient formula of a function y = f(x) is,
[ f(x + h) - f(x) ] / h
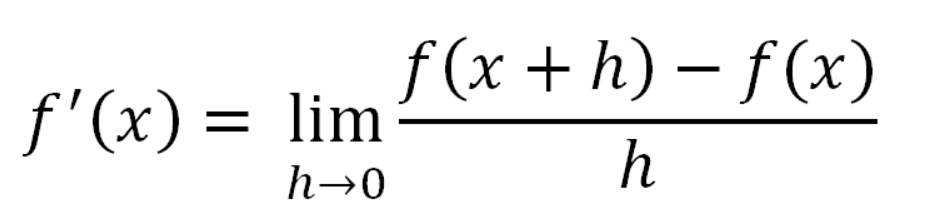
where,
- f (x + h) is obtained by replacing x by x + h in f(x)
- f(x) is the actual function
Difference Quotient Formula Derivation
Let us consider a function y = f(x) and let a secant line pass through two points of the curve (x, f(x)) and (x + h, f(x + h)). Thus using the slope formula the slope of the secant line is,
[ f(x + h) - f(x) ] / [ (x + h) - x] = [ f(x + h) - f(x) ] / h [Since the slope of any straight line = change in y/ change in x.)
This is nothing but the difference quotient formula.
Note: As h → 0, the secant of y = f(x) becomes a tangent to the curve y = f(x). Thus, as h → 0, the difference quotient gives the slope of the tangent and hence it gives the derivative of y = f(x). i.e.,
f ' (x) = lim h→0 [ f(x + h) - f(x) ] / h
Difference Quotient Formula Examples
Example 1 : Find the Difference Quotient using Difference Quotient
Consider the function f(x) = 2x^2 - 3.
Using the difference quotient formula:
Difference quotient of f(x) = [f(x + h) - f(x)] / h
= [(2(x + h)^2 - 3) - (2x^2 - 3)] / h
= [(2x^2 + 4xh + 2h^2 - 3) - 2x^2 + 3] / h
= (4xh + 2h^2) / h
= h(4x + 2h) / h
= 4x + 2h
Example 2: Finding the Derivative using Difference Quotient
Now, let's find the derivative of f(x) = 2x^2 - 3 by applying the limit as h approaches 0 to the difference quotient:
f'(x) = lim (h -> 0) (4x + 2h) = 4x + 2(0) = 4x
So, the derivative of f(x) = 2x^2 - 3 is f'(x) = 4x.
Example 3: Calculating the Difference Quotient using Difference Quotient
Let's find the difference quotient of the function f(x) = ln(x) using the difference quotient formula:
Difference quotient of f(x) = [f(x + h) - f(x)] / h
= [ln(x + h) - ln(x)] / h
= ln((x + h) / x) / h
So, the difference quotient of f(x) = ln(x) is ln((x + h) / x) / h.
Difference Quotient Formula Applications
These examples illustrate the use of the difference quotient formula to find the difference quotient and subsequently the derivative of different functions.
The Difference Quotient Formula has various applications in mathematics, science, engineering, and economics. Here are some common applications:
Calculus and Differential Equations: The primary application of the Difference Quotient Formula is in calculus, where it is used to calculate derivatives. Derivatives are essential in understanding how functions change and finding maximum and minimum values. They are also used in solving differential equations, which have widespread applications in physics, engineering, and many other fields.
Physics: In physics, the Difference Quotient Formula is used to analyze motion and rates of change. It's applied to calculate velocities, accelerations, and other physical quantities that involve changes over time or distance.
Engineering: Engineers use derivatives extensively to optimize designs and systems. The Difference Quotient helps in determining how small changes in parameters affect the performance of systems and structures, such as in electrical circuits, control systems, and mechanical engineering.
Economics: Economists use derivatives and the Difference Quotient Formula to model and analyze economic systems. It helps in understanding how changes in variables like supply, demand, and interest rates impact economic outcomes.
Statistics: In statistics, the Difference Quotient is used for numerical differentiation in cases where data is discrete. For example, it can be used to estimate the rate of change in a time series or to calculate the slope of a curve in regression analysis.
Numerical Analysis: The Difference Quotient is essential in numerical analysis for approximating derivatives and integrals when analytical solutions are not readily available. Techniques like finite differences and numerical integration rely on this formula.
Machine Learning: In machine learning and optimization algorithms, derivatives are used to update model parameters during training. The Difference Quotient can be applied to compute gradients, which guide the optimization process in neural networks and other machine learning models.
Finance: In financial modeling, derivatives are used to calculate risk measures, such as the sensitivity of an option's price to changes in underlying asset values (Greeks). The Difference Quotient is used to estimate these sensitivities in pricing and risk management.
Biology and Chemistry: In biological and chemical modeling, the Difference Quotient helps estimate reaction rates, enzyme kinetics, and how concentrations change over time in chemical reactions.
Geophysics and Earth Sciences: In studying seismic data or geological processes, the Difference Quotient can be used to estimate gradients and rates of change, aiding in understanding subsurface structures and earthquake mechanisms.
Image Processing: In image processing, derivatives are used for edge detection and feature extraction. The Difference Quotient can be applied to calculate gradients that help identify boundaries and patterns in images.
| Related Links | |
| Diagonal of a Square Formula | Diagonal Formula |
| Difference of Cubes Formula | Derivative Formula |
Difference Quotient Formula










