The
Diagonal Formula
is a mathematical formula used to calculate the length of the diagonal of a rectangle. In a rectangle, the diagonal is the line segment that connects two opposite corners of the rectangle.
If you know the length (L) and width (W) of the rectangle, you can use the Pythagorean Theorem to find the length of the diagonal (D) using the diagonal Formula. The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
A polygon is a closed two-dimensional shape formed by connecting three or more straight line segments. Some common examples of polygons include triangles, squares, rectangles, pentagons, and hexagons.
In a polygon, the individual straight line segments are referred to as its sides. The points where these segments meet are called vertices. Sides that share a common vertex are known as adjacent sides. A diagonal is a straight line segment that connects two nonadjacent vertices of the polygon.
What is Diagonal?
In a polygon, a diagonal is a line segment that connects one vertex to another vertex, and these two vertices are not adjacent to each other. For example, in a triangle, there are no diagonals because you cannot draw a line from one interior angle to any other interior angle without also including one of the sides of the triangle.
As we move to more complex polygons, such as a quadrilateral (four-sided polygon) or a pentagon (five-sided polygon), the number of diagonals increases. A quadrilateral has two diagonals, while a pentagon has five diagonals.
The concept of diagonals becomes clearer when you visualize them in various polygon shapes, as shown in the images below:
There are diagonal formulas available to calculate the number of diagonals in a polygon, which can help determine this count based on the number of sides in the polygon.
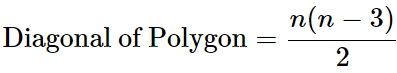
Where:
n represents the number of sides of the polygon.
The Number of Diagonals in Different Polygons
Here's a list of the number of diagonals in different polygons as calculated using the formula mentioned earlier:
Diagonal Formula of Square
The diagonal of a square can be calculated using the Pythagorean theorem because a square is a special type of rectangle with all sides of equal length.
Let's say the side length of the square is "s." To find the length of the diagonal "d," you can use the following formula:
d = s√2
Where:
"d" is the length of the diagonal.
"s" is the side length of the square.
√2 represents the square root of 2.
So, to find the diagonal of a square, simply multiply the side length by the square root of 2.
Also Check –
Logarithm Formula
Diagonal Formula of a Rectangle
The diagonal of a rectangle, you can use the Pythagorean theorem, just as you would for any right-angled triangle. In a rectangle, the diagonal is the hypotenuse of a right triangle formed by the length and width of the rectangle.
Let "L" represent the length of the rectangle, and "W" represent the width of the rectangle. The formula to calculate the diagonal "D" is as follows:
D = √(L
2
+ W
2
)
Where:
"D" is the length of the diagonal.
"L" is the length of the rectangle.
"W" is the width of the rectangle.
√ represents the square root.
By plugging the values of the length and width of the rectangle into this formula, you can find the length of the diagonal.
Diagonal Formula of a Parallelogram
In a parallelogram, the diagonal can be calculated using the Pythagorean theorem because it forms a right triangle with two adjacent sides of the parallelogram. Let's denote the length of the two adjacent sides as "a" and "b," and the length of the diagonal as "d." The formula to calculate the diagonal of a parallelogram is as follows:
d = √(a
2
+ b
2
+ 2abcos(θ))
Where:
"d" is the length of the diagonal.
"a" and "b" are the lengths of the two adjacent sides.
"θ" is the angle between the two adjacent sides.
√ represents the square root.
"cos(θ)" is the cosine of the angle θ.
Please note that you need to know both the lengths of the adjacent sides and the measure of the angle between them to use this formula effectively.
Also Check –
Introduction to Graph Formula
Diagonal Formula of a Cube
Formula to find the length of the diagonal of a cube with side length "s" is as follows:
Diagonal (d) = s√3
So, the diagonal of a cube is equal to the side length "s" multiplied by the square root of 3.
Diagonal Formula of Cuboid
The diagonal of a cuboid (also known as a rectangular prism), you can use the Pythagorean theorem. In a cuboid, the diagonal runs through the three-dimensional space, connecting two opposite corners of the cuboid.
Let "l," "w," and "h" represent the length, width, and height of the cuboid, respectively. The formula to calculate the diagonal "d" is as follows:
d = √(l
2
+ w
2
+ h
2
)
Where:
"d" is the length of the diagonal.
"l" is the length of the cuboid.
"w" is the width of the cuboid.
"h" is the height of the cuboid.
√ represents the square root.
By plugging the values of the length, width, and height of the cuboid into this formula, you can find the length of the diagonal.
Diagonal Formula Examples
Example 1:
Calculate the diagonal of a rectangle with a length of 8 cm and a width of 6 cm.
Solution:
To find the diagonal of a rectangle with a length of 8 cm and a breadth of 6 cm, you can use the diagonal formula for a rectangle:
Diagonal (D) = √(Length^2 + Breadth^2)
Plugging in the values:
D = √(8
2
+ 6
2
)
D = √(64 + 36)
D = √100
D = 10 cm
So, the diagonal of the rectangle is 10 cm.
Example 2:
Determine the diagonal length of a cube with a side length of 10 cm.
Solution:
To determine the diagonal length (d) of a cube with a side length (s) of 10 cm, you can use the formula for the diagonal of a cube:
d = s√3
Plugging in the given side length:
d = 10 cm × √3
Now, calculate the value:
d ≈ 10 cm × 1.732 (rounded to three decimal places for √3)
d ≈ 17.32 cm
So, the diagonal length of the cube is approximately 17.32 cm.
Also Check –
Data Handling Formula
Non-Mathematical Uses of the Concept of Diagonal
The concept of diagonals has diverse applications in various fields, as you've highlighted:
-
Engineering and Construction:
Diagonal bracing is crucial for providing structural stability in buildings, scaffolding, and other structures. Diagonal elements in truss structures, for example, help distribute forces and maintain stability.
-
Tools and Manufacturing:
Diagonal pliers, often called "diagonals" or "wire cutters," are commonly used in electrical work and other applications to cut wires and cables. They get their name from the diagonal cutting edges at the jaws.
-
Lashing and Knot Tying:
Diagonal lashing is a technique used in activities like camping, scouting, and construction to secure spars or poles together. It's an essential skill for creating sturdy structures with timber.
-
Sports:
In sports like football (soccer), the diagonal system of control is used by referees and assistant referees to ensure proper positioning on the field. This positioning helps officials make accurate calls and monitor the game effectively.
Understanding the concept of diagonals in these contexts is crucial for safety, precision, and efficiency in various industries and activities.
