
Derivative Formula is a fundamental concept in calculus that measures how a function changes as its input (independent variable) changes. It provides information about the rate of change of a function, which can be interpreted as the slope of the function's graph at a specific point. The derivative formula is essential for understanding the behavior of functions and solving various real-world problems.
Derivative Formula
The derivative formula is defined as a function f(x) with respect to the variable x is denoted as f'(x) or dy/dx and is defined as the limit of the average rate of change as the interval Δx approaches zero:
What is a Derivative Formula?
The derivative formula you mentioned is indeed a fundamental rule in calculus, known as the power rule. It allows us to find the derivative of a function f(x) = x^n, where 'n' can be any real number, not just integers or rational fractions. The power rule states:
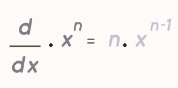
This formula tells us that when you have a term x n in a function, you can find its derivative by multiplying it by 'n' and then subtracting 1 from the exponent.
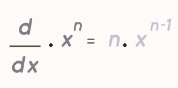
The power rule is just one of the many rules and techniques used for differentiation in calculus, but it's a fundamental and frequently used one. It allows us to find the slopes (or rates of change) of various functions, making it a crucial tool for analyzing how quantities change with respect to one another.
Derivative Formula Rules
The basic derivative formulas, which are fundamental rules used in calculus. Here they are:

Also Check: Derivatives Formula
Derivative Formula Derivation
If we have a function f(x) defined on an open interval containing a point x₀, then we say that f(x) is differentiable at the point x₀, and we represent its derivative as follows:
f'(x)= lim Δx→0 Δy/Δx
This can be expressed as:
f'(x)= lim Δx→0 [f(
The derivative of the function y = f(x) can also be denoted as f′(x) or y′(x). Additionally, Leibniz's notation is commonly used to represent the derivative of the function y = f(x) as df(x)/dx or dy/dx.
These notations and concepts help us understand how a function changes with respect to its independent variable 'x' and are fundamental in calculus.
Also Check: Determinants Formula
Derivative Formula List
Some important derivative formulas are used in mathematics, including calculus and trigonometry. These derivative formulas are essential for understanding the rates of change, slopes, and various aspects of functions. They are derived from the fundamental principles of differentiation.
Derivative Formula of Elementary Functions
Derivative Formulas of Elementary Functions The derivative formulas of elementary functions refer to the rules or mathematical expressions that allow you to calculate the derivative (rate of change) of a function with respect to its independent variable. These elementary functions and their derivative formulas are fundamental in calculus and play a crucial role in analyzing and understanding the behavior of functions.
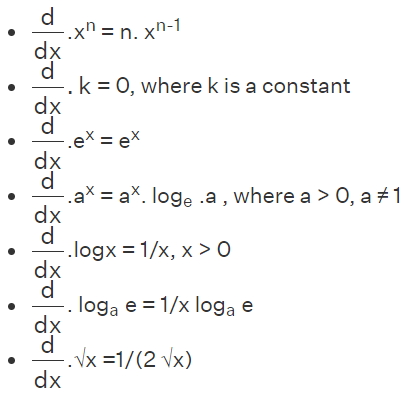
Derivative Formulas of Trigonometric Functions
The derivative formulas of trigonometric functions are rules that provide a way to calculate the derivative (rate of change) of trigonometric functions with respect to their independent variable, typically denoted as x. These formulas are essential in calculus and mathematical analysis for analyzing the behavior of trigonometric functions and solving various mathematical and scientific problems involving periodic phenomena.

Derivative Formulas of Hyperbolic Functions
The derivative formulas of hyperbolic functions are rules that provide a way to calculate the derivative (rate of change) of hyperbolic functions with respect to their independent variable, typically denoted as x. Hyperbolic functions are analogs of trigonometric functions and are used in various mathematical and scientific contexts, especially in areas like physics, engineering, and mathematics dealing with exponential growth and decay.
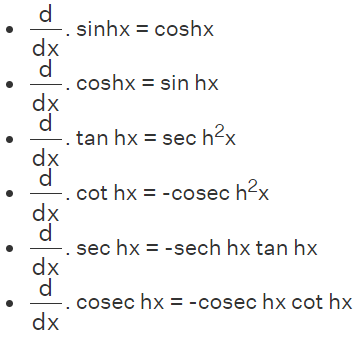
Derivative Formula Inverse Trigonometric Functions
Differentiating inverse trigonometric functions involves finding the derivative of a function that is the inverse of a trigonometric function. Here are the differentiation formulas for some common inverse trigonometric functions:
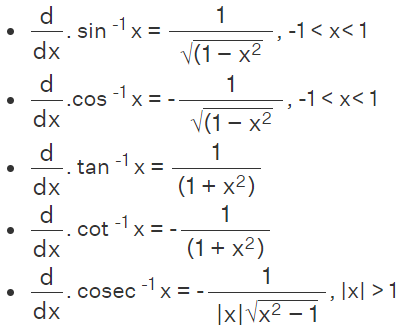
Derivative Formula of Inverse Hyperbolic Functions
Differentiating inverse hyperbolic functions involves finding the derivative of a function that is the inverse of a hyperbolic function. Here are the differentiation formulas for some common inverse hyperbolic functions.
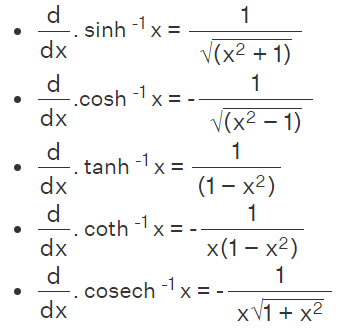
Also Check: Matrices Formula
Derivative Formula Solved Examples
Example 1 : Find the derivative of x 7 using the derivative formula.
Solution: Using the derivative formula, which states that d/dx(x n ) = n. x n-1 , we can find the derivative of x 7 :
d/dx .x 7 = 7.x 6 = 7x 6
Therefore, the derivative of x^7=7x 6
Example 2 : Differentiate 1/√x using the derivative formula.
Solution: To find the derivative of 1/√x, we can apply the derivative formula. First, rewrite 1/√x as x^(-1/2):
d/dx(1/√x) = d/dx(x^(-1/2))
Now, apply the derivative formula, d/dx(x^n) = n * x^(n-1):
d/dx(x^(-1/2)) = (-1/2) * x^((-1/2)-1)
Simplify the exponent:
d/dx(x^(-1/2)) = (-1/2) * x^(-3/2)
Now, rewrite it as a fraction:
d/dx(x^(-1/2)) = -1/(2 * √x)
So, the derivative of 1/√x is -1/(2x√x).
Example 3: Find the derivative of y = Cos^2(x) using the derivative formula.
Solution: Let's use a substitution to simplify the problem. Let t = Cos(x). Then, y = t 2 .
Now, find the derivative of y with respect to t using the power rule, which states that d/dt(t^n) = n * t^(n-1):
dy/dt = 2 t (2-1) = 2t
Next, find the derivative of t with respect to x using the chain rule, which states that if y = f(g(x)), then dy/dx = (dy/dt) * (dt/dx):
dt/dx = -sin(x) (derivative of Cos(x))
Now, apply the chain rule:
dy/dx = (dy/dt) * (dt/dx) = (2t) * (-sin(x)) = -2t * sin(x)
But we know that t = Cos(x), so:
dy/dx = -2 * Cos(x) * sin(x)
So, the derivative of y = Cos^2(x) is -2 * Cos(x) * sin(x), or simply, -sin(2x).
| Related Links | |
| Decimal to Fraction Formula | Cost Price Formula |
| Decay Formula | Calculus Formula |
Derivative Formula FAQs
Q1. What is a derivative in calculus?
Q2. What is the derivative formula for a constant?
Q3. What is the power rule for derivatives?
Q4. How do you find the derivative of a sum of functions?
Q5. What is the chain rule in calculus?










