Diffraction Grating Formula - Definition, Applications
A Diffraction Grating formula is an optical component that is used to disperse light into its constituent colors, Diffraction gratings are commonly used in devices like spectrometers, monochromators.
Murtaza Mushtaq26 Sept, 2023
Share
A diffraction grating is an optical component that is used to disperse light into its constituent colors or wavelengths. It consists of a large number of equally spaced, parallel slits or rulings that are closely packed together. When light passes through a diffraction grating, it undergoes a phenomenon called diffraction, which results in the separation of light into its various spectral components. In this article, we will explore the diffraction grating formula in detail, discussing its components, applications, and the physics behind it.
Introduction to Diffraction Grating
A diffraction grating is a powerful tool in optics and spectroscopy. It is designed to separate incoming light into its individual wavelengths or colors, which is essential for applications such as spectroscopy, where the analysis of light's spectral composition is crucial. Diffraction gratings are commonly used in devices like spectrometers, monochromators, and other optical instruments for this purpose.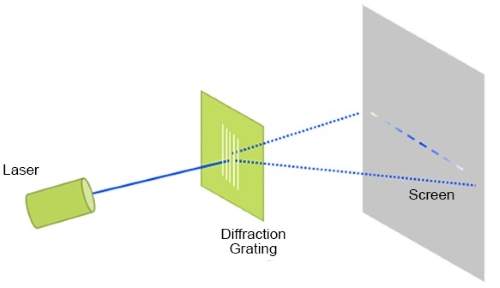
How Diffraction Gratings Formula Work?
Diffraction gratings work based on the principle of diffraction, which is the bending of light as it encounters an obstacle or aperture. When light passes through the narrow slits or rulings of a diffraction grating, it undergoes diffraction, causing the light waves to interfere with each other constructively and destructively. This interference pattern results in the dispersion of light into its various wavelengths.Also Check - Heat Gain Formula
The key factors that determine the characteristics of the diffraction pattern produced by a grating are: - Wavelength of light (λ): The wavelength of the incident light is a crucial factor. Different wavelengths will be separated by different angles, allowing the grating to act as a spectral disperser. - Spacing of the grating (d): The distance between adjacent rulings or slits on the grating is known as the grating spacing. It plays a significant role in determining the angles at which different wavelengths are diffracted. - Order of diffraction (m): Diffraction can occur at different orders, labeled as m. The zeroth order (m = 0) corresponds to undiffracted light, while positive and negative orders represent different orders of diffraction. Higher orders result in greater angular separation between wavelengths.Also Check - Fluid Dynamics Formula
Formula Of Diffraction Grating
- The Diffraction Grating Equation:
Also Check - Induced Voltage Formula
4. Applications of Diffraction Grating
Diffraction gratings have a wide range of applications across various fields. Some of the notable applications include: - Spectroscopy : Diffraction gratings are fundamental components in spectrometers used for chemical analysis, astronomy, and materials characterization. They enable the separation and measurement of the spectral lines emitted or absorbed by different substances. - Wavelength Selection: In lasers, diffraction gratings formula are used to select specific wavelengths, allowing for the tuning of laser output. This is crucial in applications like telecommunications and medical devices. - Color Separation: In optics and photography, diffraction gratings are used to separate colors, as seen in some camera lenses and optical filters. - Astronomy: Gratings are used in astronomical spectrographs to analyze the light emitted or absorbed by celestial objects, helping scientists determine their chemical composition, temperature, and other properties. - Light Analysis: In physics experiments, gratings are used to study the behavior of light and validate theories related to wave optics.Also Check - Hubbles Law Formula
5. Understanding the Diffraction Grating Equation
Let's dive deeper into the components of the diffraction grating formula equation and understand how it works: Order of Diffraction (m): The order of diffraction (m) is an integer value that indicates which diffraction order you are interested in. The zeroth order (m = 0) corresponds to the undiffracted, central beam. Positive integers (m = 1, 2, 3, ...) represent higher orders on one side of the central beam, while negative integers (m = -1, -2, -3, ...) represent orders on the other side. Higher diffraction orders are farther from the central beam and result in greater angular separation between wavelengths. For example, the first-order (m = 1) diffraction angle will be larger than the second-order (m = 2) angle for the same wavelength. Wavelength of Light (λ): The wavelength of light (λ) is the distance between successive peaks (or troughs) of a light wave. It is typically measured in nanometers (nm) or angstroms (Å). Different colors of light have different wavelengths. For example, red light has a longer wavelength than blue light. Grating Spacing (d): The grating spacing (d) is the distance between adjacent rulings or slits on the diffraction grating. It is a crucial parameter that determines the angular dispersion of light. A smaller grating spacing will result in a larger angular separation between wavelengths. Angle of Diffraction (θ): The angle of diffraction (θ) is the angle between the incident light direction and the direction of the diffracted light. It is measured in radians. The diffraction angle depends on both the wavelength of light and the order of diffraction, as given by the diffraction grating equation.6. Practical Considerations:
In practice, when using a diffraction grating formula, you typically know the wavelength of the incident light (λ) and the order of diffraction (m) you are interested in. You can then use the diffraction grating equation to calculate the angle of diffraction (θ) and determine where the diffracted light will be observed.Here are some practical considerations:
- Calibration: To accurately measure wavelengths, you need to calibrate your diffraction grating formula setup. This often involves using known spectral lines or sources of known wavelength to establish a relationship between the angle of diffraction and wavelength. - Higher Orders: Higher-order diffractions can be used to disperse light over a wider range of angles, but they are also farther from the central beam and can be weaker in intensity. - Grating Efficiency: Not all incident light is diffracted by the grating. Some of it is lost through absorption or reflection. Grating efficiency is a measure of how effectively a grating disperses light and can vary with the design and manufacturing of the grating. - Blazing: Some gratings are designed to maximize efficiency at a particular wavelength or order of diffraction. This is known as blazing, and it involves optimizing the groove profile of the grating.Diffraction Grating Formula FAQs
What is the purpose of a diffraction grating in spectroscopy?
A diffraction grating is used in spectroscopy to disperse incoming light into its individual wavelengths or colors. This dispersion allows scientists to analyze the spectral composition of light emitted or absorbed by a sample. Spectroscopy is widely used in various fields, including chemistry, astronomy, and materials science, for identifying elements, compounds, and physical properties of substances.
How does the diffraction grating equation help in wavelength determination?
The diffraction grating equation (mλ = d sin(θ)) relates the wavelength of light (λ), the order of diffraction (m), the grating spacing (d), and the diffraction angle (θ). By knowing any three of these parameters and the diffraction grating equation, you can calculate the fourth. This equation is essential for determining the wavelength of light based on the angle of diffraction and the grating's characteristics, making it a key tool in spectroscopy.
Are there different types of diffraction gratings, and how do they differ?
Yes, there are different types of diffraction gratings, including transmission gratings, reflection gratings, volume phase holographic gratings, and replica gratings. They differ in how they interact with light. For example, transmission gratings allow light to pass through, while reflection gratings reflect light off their surface. Each type has specific advantages and disadvantages, making them suitable for various applications.
What is spectral resolution, and why is it important in spectroscopy?
Spectral resolution refers to the ability of a spectroscopic instrument to distinguish between closely spaced wavelengths or spectral lines. It is a crucial parameter in spectroscopy because it determines the instrument's ability to detect fine spectral features and resolve overlapping lines. High spectral resolution is essential when studying complex spectra or when precise identification of spectral lines is required.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.