Important Questions for Class 10 Maths Chapter 9 Applications of Trigonometry
Ananya Gupta19 Feb, 2024
Share
Important Questions for Class 10 Maths Chapter 9: Trigonometry is very important chapter in Class 10. While some might perceive it as complex initially, once you grasp the fundamentals, it becomes much more manageable, allowing you to tackle various levels of difficulty with ease. Regular practice is key to mastering any mathematical concept, including trigonometry. Its applications are widespread in everyday scenarios, making it a practical skill to possess. Moreover, it is a high-scoring topic in board exams, particularly in Class 10 Maths Chapter 9. A solid understanding of this topic can greatly enhance your exam performance.
Important Questions for Class 10 Maths Chapter 9 Trigonometry are available at Physics Wallah. The questions follow the most recent exam format and the updated curriculum. These important questions from the trigonometry chapter are also available for download in PDF format for the convenience of students. Students preparing for the CBSE Class 10 board exams are advised to review these Trigonometry questions to maximize their marks in this chapter.Important Questions for Class 10 Maths Chapter 9 Overview
In Chapter 9 of Class 10 Mathematics, there are some really important questions to focus on. These questions are designed to help students prepare well for their exams. The chapter is mainly about using trigonometry to solve problems related to heights and distances. It includes situations where you need to figure out angles like looking up or down. By practicing these questions, students get better at applying math to real-life situations. It is all about getting ready to do well in their Class 10 Maths exams.Important Questions for Class 10 Maths Chapter 9 Applications of Trigonometry
Q.1: A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
Using given instructions, draw a figure. Let AC be the broken part of the tree. Angel C = 30 degrees. BC = 8 m To Find: Height of the tree, which is ABQ.2: A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is :
(a) 25 2 (b) 25 3 (c) 25 (d) 12.5
Solution:
Let the height of the tower be H m.
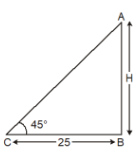
Thus, tan45°= Base/ perpendicular Or H/25 =1 Hence, H = 25m
Q.3: A ladder, leaning against a wall, makes anangle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder. (2016OD)
Solution:
Let AC be the ladder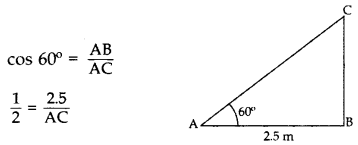
∴ Length of ladder, AC = 5 m 2.5 m
Q.4: A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then calculate the height of the wall.
Solution:
∠BAC = 180° – 90° – 60o = 30° sin 30° = BCAC 12=BC15 2BC = 15 BC = 152mQ.4: In the given figure, a tower AB is 20 m high and BC, its shadow on the ground, is 203–√ m long. Find the Sun’s altitude.
Solution:
AB = 20 m, BC = 20 3 –√ m,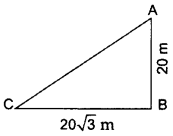
θ = ?
In ∆ABC,
Q.5: The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45° and 30°. If the ships are 200 m apart, find the height of the light house.
Solution:
Let AB be the height of the light house, D and C are two ships and DC = 200 m Let BC = x m, AB = h m In rt. ∆ABC,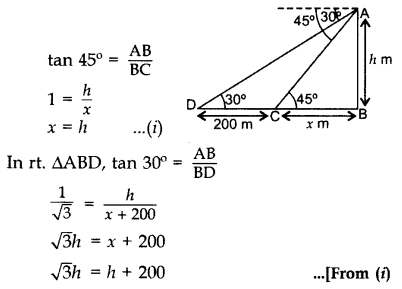
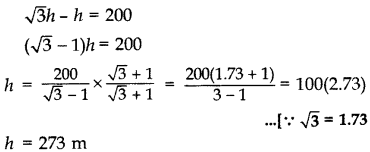∴ Height of the light house = 273 m
Q.6: The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will
(A) also get doubled (B) will get halved (C) will be less than 60 degree (D) None of theseSolution:
According to Question:
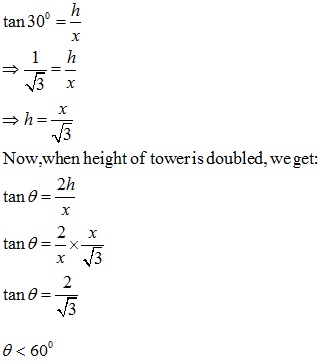
Q.7: If the height of a tower and the distance of the point of observation from its foot,both, are increased by 10%, then the angle of elevation of its top
(A) increases (B) decreases (C) remains unchanged (D) have no relation.Solution:
Since tan θ = h/x Where h is height and x is distance from tower, If both are increased by 10%, then the angle will remain unchanged.Q.8: As observed from the top of a 60 m high light house from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the light-house, find the distance between the two ships. (Use 3 –√ = 1.732]
Solution:
Let AB = 60 m be the height of Light-house and C and D be the two ships. In right ∆ABC,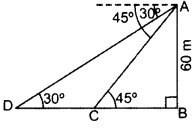
∴ Distance between the two ships,
CD = BD – BC = 103.92 – 60 = 43.92 m
Q.9: The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 30°. If the aeroplane is flying at a constant height of 3000 3 –√ m, find the speed of the aeroplane.
Solution:
Let A be the point on the ground and C be the aeroplane. In rt. ∆ABC,
Q.10: From the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45° and 60° respectively. Find the height of the tower. (Take 3 –√ = 1.73] (2014OD)
Solution:
Let AC be the building & DE be the tower.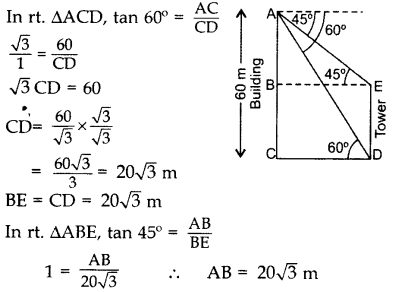
∴ Height of the tower, DE = BC
DE = AC – AB
DE = 60 – 20
3
–√
= 20(3 –
3
–√
)
DE = 20(3 – 1.73) = 20(1.27)
DE = 25.4 m
Q.11. The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building. [Use 3 –√ = 1.73].
Solution:
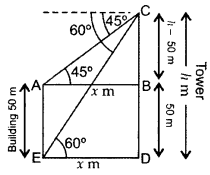Let AE be the building and CD be the tower. Let height of the tower = h m
and, the horizontal distance between tower and building = x m …[Given
BD = AE = 50 m
∴ BC = CD – BD = (h – 50) m
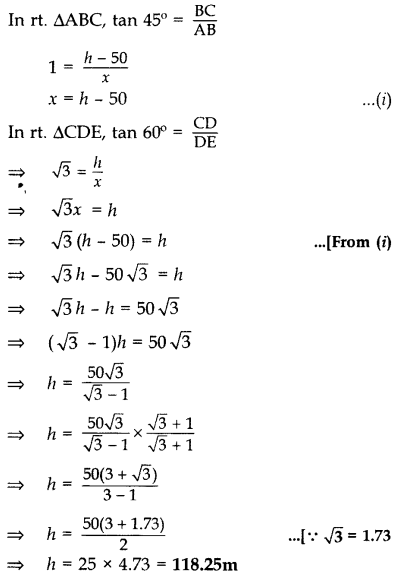From (i), x = h – 50
= 118.25 – 50 = 68.25 m
Height of the tower, h = 118.25 m
∴ Horizontal distance between tower and Building, x = 68.25 m
Q.12: A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill. (2016D)
Solution:
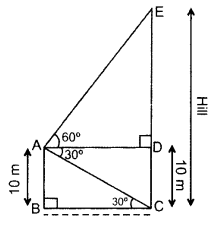Let the man standing on the deck of a ship be at point A and let CE be the hill.
Here BC is the distance of hill from ship and CE be the height of hill.
In rt. ∠ABC, tan 30° =
A
B
B
C
BC = 10
3
–√
m .(i)
BC = 10(1.73) = 17.3 m …[::
3
–√
= 1.73
AD = BC = 10
3
–√
m …(ii) [From (i)
In rt. ∆ADE, tan 60° =
D
E
A
D
⇒
3
–√
=
D
E
10
3
√
… [From (ii)
⇒ DE = 10
3
–√
×
3
–√
= 30 m
∴ CE = CD + DE = 10 + 30 = 40 m
Hence, the distance of the hill from the ship is 17.3 m and the height of the hill is 40 m.
Q.13: From the top of a tower 100 m high, a man observes two cars on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the cars. (Use 3 –√ = 1.732]
Solution:
Let AB be the tower. In rt. ∆ABC, tan 45° = A B B C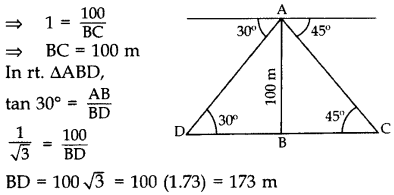
∴ Distance between the cars, CD
= BD + BC
= 173 + 100
= 273 m
Q.14: Two poles of equal heights are standing opposite to each other on either side of the road, which is 100 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles.
Solution:
Let AB and DE be the two equal poles and C be the point on BD (road). Let BC = x m Then CD = (100 – x) m Let AB = DE = y m In rt. ∆ABC,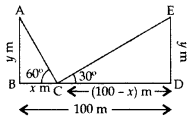
⇒ 3y = 100
3
–√
– y
⇒ 4y = 100
3
–√
∴ Height of the poles,
y =
100
3
√
4
= 25
3
–√
m = 25(1.73) = 43.25 m
Q.15: The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB = 50 m be the tower and CD be the building. In rt. ∆ABC,
Benefits of Solving Important Questions for Class 10 Maths Chapter 9
Understanding Concepts: By solving these questions, students grasp the fundamental concepts of trigonometry applied to real-life scenarios, such as heights and distances.
Improved Problem-Solving Skills: Practicing these questions enhances students problem-solving abilities, as they learn to apply trigonometric principles to various situations involving heights and distances.
Increased Confidence: As students solve these questions, their confidence in their mathematical abilities grows, boosting their overall performance in mathematics.
Application in Daily Life: Understanding how trigonometry relates to everyday situations like measuring heights and distances helps students see the practical applications of mathematics in the real world.
Preparation for Competitive Exams: Many of the concepts covered in Class 10 Maths Chapter 9 are relevant to competitive exams like JEE, making solving these questions valuable for future academic pursuits.
Important Questions for Class 10 Maths Chapter 9 FAQs
Is trigonometry hard in class 10?
Can these trigonometry questions help me prepare for competitive exams?
Who invented trigonometry?
Is Ncert trigonometry enough?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
