Solution:
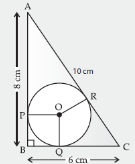
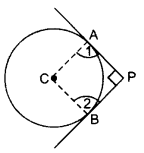 Construction: Join AC and BC.
Proof: ∠1 = ∠2 = 90° ….[Tangent is I to the radius (through the point of contact
∴ APBC is a square.
Length of each tangent
= AP = PB = 4 cm
= AC = radius = 4 cm
Construction: Join AC and BC.
Proof: ∠1 = ∠2 = 90° ….[Tangent is I to the radius (through the point of contact
∴ APBC is a square.
Length of each tangent
= AP = PB = 4 cm
= AC = radius = 4 cm
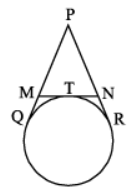
Q.7: In the given figure, PQ and PR are two tangents to a circle with Centre O. If ∠QPR = 46°, then calculate ∠QOR.
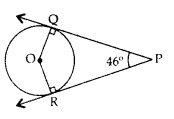
Solution:
∠OQP = 900 ∠ORP = 90° ∠OQP + ∠QPR + ∠ORP + ∠QOR = 360° …[Angle sum property of a quad. 90° + 46° + 90° + ∠QOR = 360° ∠QOR = 360° – 90° – 46° – 90° = 134°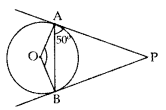 ∠PBA = ∠PAB = 50° …[Angles equal to opposite sides
In ∆ABP, ∠PBA + ∠PAB + ∠APB = 180° …[Angle-sum-property of a ∆
50° + 50° + ∠APB = 180°
∠APB = 180° – 50° – 50° = 80°
In cyclic quadrilateral OAPB
∠AOB + ∠APB = 180° ……[Sum of opposite angles of a cyclic (quadrilateral is 180°
∠AOB + 80o = 180°
∠AOB = 180° – 80° = 100°
∠PBA = ∠PAB = 50° …[Angles equal to opposite sides
In ∆ABP, ∠PBA + ∠PAB + ∠APB = 180° …[Angle-sum-property of a ∆
50° + 50° + ∠APB = 180°
∠APB = 180° – 50° – 50° = 80°
In cyclic quadrilateral OAPB
∠AOB + ∠APB = 180° ……[Sum of opposite angles of a cyclic (quadrilateral is 180°
∠AOB + 80o = 180°
∠AOB = 180° – 80° = 100°
 Radius of the circle
=
3
c
m
Join OA and OP
Also, OP is a bisector line of
∠
APC
∴
∠
A
P
O
=
∠
C
P
O
=
30
∘
O
A
⊥
A
P
Also, tangents at any point of a circle is perpendicular to the radius through the point of contact.
In right angled
Δ
O
A
P
,
we have
tan
30
∘
=
O
A
A
P
=
3
A
P
⇒
1
√
3
=
3
A
P
⇒
A
P
=
3
√
3
c
m
A
P
=
C
P
=
3
√
3
c
m
[Tangents drawn from an external point are equal]
Hence, the length of each tangent is
3
√
3
c
m
.
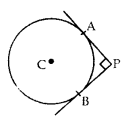
Radius of the circle
=
3
c
m
Join OA and OP
Also, OP is a bisector line of
∠
APC
∴
∠
A
P
O
=
∠
C
P
O
=
30
∘
O
A
⊥
A
P
Also, tangents at any point of a circle is perpendicular to the radius through the point of contact.
In right angled
Δ
O
A
P
,
we have
tan
30
∘
=
O
A
A
P
=
3
A
P
⇒
1
√
3
=
3
A
P
⇒
A
P
=
3
√
3
c
m
A
P
=
C
P
=
3
√
3
c
m
[Tangents drawn from an external point are equal]
Hence, the length of each tangent is
3
√
3
c
m
.
Q.10: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Solution:
 Given:
A
circle with center
O
Given:
A
circle with center
O
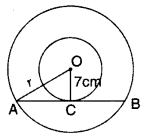 Given: OC = 7 cm, AB = 48 cm
To find: r = ?
∠OCA = 90° ..[Tangent is ⊥ to the radius through the point of contact
∴ OC ⊥ AB
AC =
1
2
(AB) … [⊥ from the centre bisects the chord
⇒ AC =
1
2
(48) = 24 cm
In rt. ∆OCA, OA
2
= OC
2
+ AC
2
… [Pythagoras’ theorem
r
2
= (7)
2
+ (24)
2
= 49 + 576 = 625
∴ r=
625
−−−√
= 25 cm
Given: OC = 7 cm, AB = 48 cm
To find: r = ?
∠OCA = 90° ..[Tangent is ⊥ to the radius through the point of contact
∴ OC ⊥ AB
AC =
1
2
(AB) … [⊥ from the centre bisects the chord
⇒ AC =
1
2
(48) = 24 cm
In rt. ∆OCA, OA
2
= OC
2
+ AC
2
… [Pythagoras’ theorem
r
2
= (7)
2
+ (24)
2
= 49 + 576 = 625
∴ r=
625
−−−√
= 25 cm
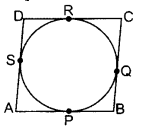 AB = CD
and AD = BC ..(i)
AP = AS …[Tangents drawn from an external point are equal in length
PB = BQ
CR = CO
DR = DS
By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC … [From (i)
2AB = 2 BC
AB = BC …(ii)
From (i) and (ii), AB = BC = CD = DA
∴ ॥
gm
ABCD is a rhombus.
AB = CD
and AD = BC ..(i)
AP = AS …[Tangents drawn from an external point are equal in length
PB = BQ
CR = CO
DR = DS
By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC … [From (i)
2AB = 2 BC
AB = BC …(ii)
From (i) and (ii), AB = BC = CD = DA
∴ ॥
gm
ABCD is a rhombus.
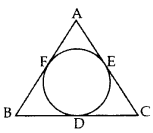
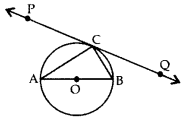
Solution:
 AB = AC
To prove: BD = CD
Proof: Since the lengths of tangents drawn from an external point to a circle are equal
∴ AF = AE … (i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC … [Given
∴ CD = BD
AB = AC
To prove: BD = CD
Proof: Since the lengths of tangents drawn from an external point to a circle are equal
∴ AF = AE … (i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC … [Given
∴ CD = BD
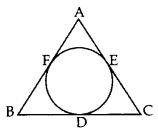
 Solution:
Solution:
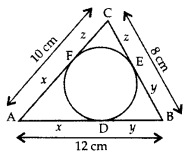
 AB = AC
To prove: BD = CD
Proof: AF = AE ..(i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC …[Given
∴ CD = BD
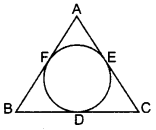
AB = AC
To prove: BD = CD
Proof: AF = AE ..(i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC …[Given
∴ CD = BD