
Isosceles trapezoids are indeed an interesting type of quadrilateral with several unique properties that set them apart from other quadrilaterals. Let's discuss these properties in detail:
Congruent Base Angles: In an isosceles trapezoid, the two base angles (the angles formed by one of the bases and one of the legs) are congruent. This means they have the same measure, and typically, they are acute angles.
Congruent Non-Parallel Sides: The non-parallel sides of an isosceles trapezoid are also congruent. This makes the trapezoid have two pairs of equal sides.
Base Lengths: The lengths of the two parallel bases (the longer and the shorter sides) are different. The longer base is opposite the longer pair of non-parallel sides, while the shorter base is opposite the shorter pair of non-parallel sides.
Diagonals: The diagonals of an isosceles trapezoid are congruent. This means that the line segments connecting the opposite vertices have the same length.
Midsegment: The midsegment of an isosceles trapezoid, which is the line segment connecting the midpoints of the two legs, is parallel to and equal in length to the average of the two bases. This midsegment divides the trapezoid into two congruent triangles.
Sum of Interior Angles: The sum of the interior angles of an isosceles trapezoid is always 360 degrees, just like any quadrilateral.
Perpendicular Diagonals: The diagonals of an isosceles trapezoid are perpendicular to each other. This means that the angle formed by the intersection of the diagonals is a right angle.
Symmetry: Isosceles trapezoids exhibit bilateral symmetry, meaning that you can fold the trapezoid along the midsegment, and both halves will coincide perfectly.
Area Formula: The area of an isosceles trapezoid can be calculated using the formula:
Area = (1/2) * (sum of the lengths of the bases) * (height)
Circumscribed Circle: An isosceles trapezoid can be circumscribed by a circle, meaning all four vertices of the trapezoid lie on the circumference of a single circle.
These unique properties make isosceles trapezoids an interesting and distinctive type of quadrilateral in geometry, and they are frequently used in various mathematical and architectural applications.
Isosceles Trapezoid Definition
An isosceles trapezoid can be defined as a trapezoid with the following characteristics:
Two opposite sides (bases) are parallel (a and b in your example).
The two non-parallel sides (legs) are of equal length (c and d in your example).
This definition captures the key properties of an isosceles trapezoid, making it easy to identify and work within geometry and other mathematical contexts. The image you mentioned is a helpful visual representation of these characteristics.
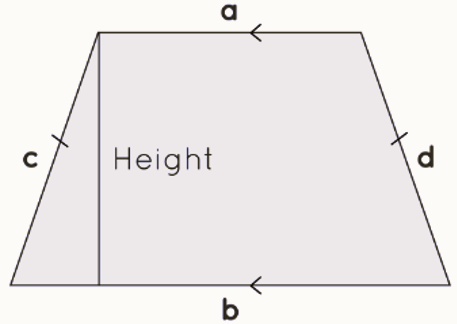
Isosceles Trapezoid Formula
The area and perimeter of an isosceles trapezoid are correct. Here's a summary of these formulas:
Area of Isosceles Trapezoid:
To calculate the area of an isosceles trapezoid, you can use the formula:
Area = (1/2) * (sum of the lengths of the parallel sides) * (height)
In this formula, the height is the perpendicular distance between the two parallel sides.
Perimeter of Isosceles Trapezoid:
To find the perimeter of an isosceles trapezoid, simply add up the lengths of all its sides:
Perimeter = sum of all sides
These formulas are useful for solving problems involving isosceles trapezoids in geometry and other mathematical contexts. Remember to use the correct measurements for the sides and height when applying these formulas.
Isosceles Trapezoid Examples
Example 1: Finding the Height
Given:
Area = 128 square inches
Bases = 12 inches and 20 inches
Using the formula for the area of an isosceles trapezoid:
Area = (1/2) * (sum of parallel sides) * height
128 = (32/2) * height
128 = 16 * height
Solving for the height:
height = 128/16 = 8 inches
Example 2: Finding the Area
Given:
Bases = 3 inches and 5 inches
Height = 4 inches
Using the formula for the area of an isosceles trapezoid:
Area = (1/2) * (sum of parallel sides) * height
Area = (8/2) * 4
Area = 16 square inches
Example 3: Finding the Perimeter
Given:
Bases = 20 inches and 25 inches
Non-parallel sides = 30 inches each
The perimeter of an isosceles trapezoid is the sum of all its sides:
Perimeter = 20 + 25 + 30 + 30 = 105 inches
These examples demonstrate how to use the formulas for isosceles trapezoids to find their height, area, and perimeter, based on the given information.
Isosceles Trapezoid Formula Application
The formulas and properties of isosceles trapezoids have various practical applications in geometry, architecture, engineering, and other fields. Here are some of the applications:
- Architectural Roof Design: Isosceles trapezoids are often used in the design of roofs. The shape allows for a sloping roof with two parallel sides and two equal-length, non-parallel sides. This design is both aesthetically pleasing and functional for shedding water and snow.
- Window Design: Certain window shapes, like dormer windows and bay windows, have isosceles trapezoidal elements. These shapes can add character and allow more natural light into a building.
- Bridges: In bridge engineering, the design of support beams can often incorporate isosceles trapezoidal elements to distribute weight and provide structural stability.
- Truss Structures: Trusses are often used in construction to support roofs and bridges. Isosceles trapezoidal truss elements can be found in the design of these structures.
- Surveying: In land surveying and cartography, isosceles trapezoids are used to calculate land area, especially when dealing with irregularly shaped plots.
| Related Links | |
| Difference Quotient Formula | Probability |
| Effect Size Formula | Consecutive Integers Formula |
Isosceles Trapezoid Formula FAQs
Q1. What is an isosceles trapezoid?
Q2. How can you identify an isosceles trapezoid?
Q3. What are the properties of an isosceles trapezoid?
Q4. How do you calculate the area of an isosceles trapezoid?
Q5. What is the formula for the perimeter of an isosceles trapezoid?










