A matrix is a structured arrangement of numbers, which can be either real or complex, organized in a rectangular grid format consisting of m horizontal lines (known as rows) and n vertical lines (known as columns). This grid is referred to as a matrix of order m by n, often denoted as an m × n matrix. The numbers within the matrix are enclosed within square brackets [ ] or parentheses ( ).
Introduction to Matrices
In a nutshell, the matrix described above can be represented by the notation A = [a
ij
] mxn. Here, the individual numbers a11, a12, and so on, are referred to as the elements of the matrix A. Each element, denoted as a
ij
, belongs to the ith row and jth column, making it the (i, j)th element of the matrix A, which is written as A = [a
ij
].
CBSE Class 10 Sample Paper
Important Formulas for Matrices
If A and B are square matrices of order n, and In is a corresponding unit matrix, then
-
A(adj.A) = | A | In = (adj A) A
-
| adj A | = |A|
n-1
(Thus A (adj A) is always a scalar matrix)
-
adj (adj.A) = | A |
n-2
A
-
adj (AB) = (adj B) (adj A)
-
adj (Am) = (adj A)m,
-
adj 0 = 0
-
A is symmetric ⇒ adj A is also symmetric
-
A is diagonal ⇒ adj A is also diagonal
-
A is triangular ⇒ adj A is also triangular
-
A is singular ⇒| adj A | = 0
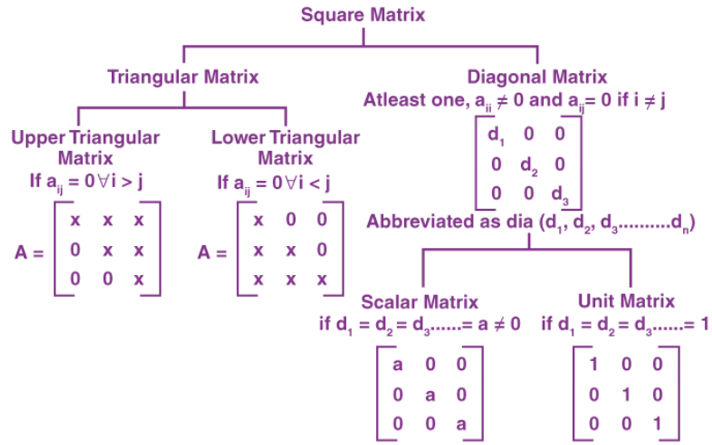
Types of Matrices
(i) Symmetric matrix: A square matrix A = [a
ij
] is called a symmetric matrix if a
ij
= a
ji
, for all i, j.
(ii) Skew-symmetric matrix: when a
ij
= – a
ji
(iii) Hermitian and skew–Hermitian matrix:
(iv) Orthogonal matrix: if AAT = In = ATA
(v) Idempotent matrix: if A2 = A
(vi) Involuntary matrix: if A2 = I or A-1 = A
(vii) Nilpotent matrix: A square matrix A is nilpotent; if Ap = 0, p is an integer.
Trace of Matrix
The trace of a square matrix is the sum of the elements on the main diagonal.
(i) tr(λA_ = λ tr(A)
(ii) tr(A + B) = tr(A) + tr(B)
(iii) tr(AB) = tr(BA)
Also Check –
Comparing Quantities Formula
Matrix Transpose
-
(AT)T= A
-
(A+B)T= AT + BT
-
(AB)T= BTAT
-
(kA)
T
= k(A)
T
-
(A1A2A3…..An-1An)
T
= A
T
n
A
t
n-1
…..A
T
3
A
T
2
A
T
1
-
I
T
= I
-
tr(A) = t(A
T
)
Properties of Matrix Multiplication
-
AB ≠ BA
-
(AB)C = A(BC)
-
A (B + C) = AB + AC
-
(A + B)C = AC + BC
Adjoint of a Matrix
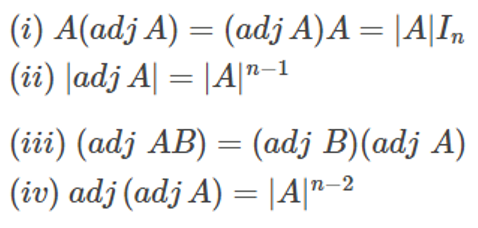
Also Check –
Congruence of Triangles
Inverse of a Matrix
A-1 exists if A is non-singular, i.e.,
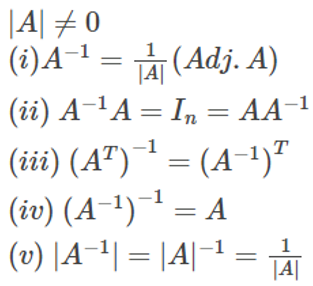
Order of a Matrix
A matrix with m rows and n columns is designated as a matrix of order m x n.
For instance, consider the following matrix:
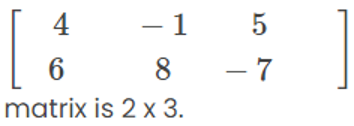
Please note the following:
(a) A matrix is simply a structured arrangement of specific quantities.
(b) The elements within a matrix can consist of real or complex numbers. If all the elements in a matrix are real numbers, it is referred to as a real matrix.
(c) An m x n matrix contains a total of m * n elements.
Illustration 1: Create a 3×4 matrix A = [aij] with elements defined as a
ij
= 2i + 3j.
In this illustration, we will build a 3×4 matrix denoted as A, where each element a
ij
is determined using the formula aij = 2i + 3j.
Solution: In this particular problem, we have 'i' representing the number of rows, and 'j' representing the number of columns. By substituting the appropriate values for rows and columns into the formula a
ij
= 2i + 3j, we can construct the desired matrix.
Using the formula a
ij
= 2i + 3j:
For the 3×4 matrix A, we can compute its elements as follows:
a11 = 2(1) + 3(1) = 5
a12 = 2(1) + 3(2) = 8
a13 = 2(1) + 3(3) = 11
a14 = 2(1) + 3(4) = 14
a21 = 2(2) + 3(1) = 7
a22 = 2(2) + 3(2) = 10
a23 = 2(2) + 3(3) = 13
a24 = 2(2) + 3(4) = 16
a31 = 2(3) + 3(1) = 9
a32 = 2(3) + 3(2) = 12
a33 = 2(3) + 3(3) = 15
a34 = 2(3) + 3(4) = 18
Using these calculations, we can construct the 3×4 matrix A with the respective values for its elements.
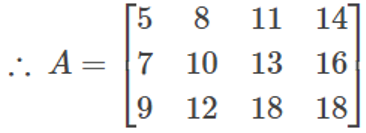
Also Check –
Cubes and Cubes Roots Formula
Trace of a Matrix
Let A = [aij]nxn and B = [bij]nxn and λ be a scalar,
(i) tr(λA) = λ tr(A)
(ii) tr(A + B) = tr(A) + tr(B)
(iii) tr(AB) = tr(BA)
Transpose of Matrix
The transformation of a given matrix A by interchanging its rows and columns results in a new matrix known as the transpose of matrix A, denoted by AT or A'. According to this definition, if the original matrix A has an order of m x n, then the order of its transpose, AT, becomes n x m.
For instance, consider the transpose of a matrix:
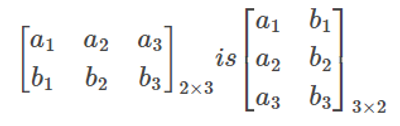
Also Check –
Factorization Formula
Properties of Transpose of Matrix
-
(AT)T= A
-
(ii) (A + B)T = AT+ BT
-
(iii) (AB)T = BTAT
-
(iv) (kA)T = k(A)T
-
IT = I
-
(vii) tr(A) = tr(AT)
