
Most Probable Speed of Gas Molecules: The kinetic theory of gases, which seeks to explain the behavior of gas molecules in motion, has unlocked various fundamental principles about their speed, collisions, and distribution. One crucial aspect of this theory is the concept of the most probable speed of gas molecules.
At the heart of the kinetic theory lies the postulate that gas molecules are in constant, random motion, colliding with each other and the walls of their container. This theory provides a framework for understanding various gas properties, including pressure, temperature, and volume, by describing the behaviour of individual gas particles.
Most Probable Speed of Gas Molecules
The most probable speed of gas molecules refers to the speed at which the greatest number of gas molecules within a gas sample move. According to the Maxwell-Boltzmann distribution, which characterises the speed distribution of gas particles in a gas sample, the most probable speed is determined by the peak of the distribution curve. It's essential to note that the distribution of molecular speeds in a gas follows a symmetrical, bell-shaped curve, often known as the Maxwell-Boltzmann distribution curve.
The root of this concept can be traced back to the work of James Clerk Maxwell and Ludwig Boltzmann, who independently contributed to the understanding of the statistical behaviour of gases in the 19th century. Their combined efforts led to the development of the statistical mechanics that underpin our understanding of gas behaviour today.
In this context, the most probable speed is not the average speed of gas molecules. Instead, it represents the speed at which the highest number of gas molecules are moving at a given temperature. It's a mode of the distribution curve where the maximum number of particles are concentrated.
Most Probable Speed of Gas Molecules Formula
The most probable speed can be mathematically derived from the Maxwell-Boltzmann distribution function, which takes into account the mass of the gas molecules and the temperature of the gas. For an ideal gas, the most probable speed (v p ) is given by the equation:
Most Probable Speed of Gas Molecules
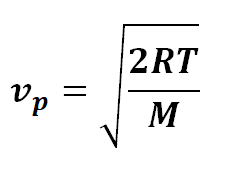
Where:
v p = most probable speed
R = ideal gas constant
T = temperature in Kelvin
M = molar mass of the gas
This equation elucidates the dependency of the most probable speed on temperature and the molar mass of the gas. As temperature increases, the most probable speed also increases. However, the relationship between most probable speed and molar mass is inverse – lighter gas molecules have higher most probable speeds compared to heavier ones at the same temperature.
Applications of Most Probable Speed of Gas Molecules
The understanding of the most probable speed of gas molecules has profound implications in various fields, including physics, chemistry, and engineering. It assists in comprehending diffusion rates, chemical reactions, and the behavior of gases under different conditions, contributing to advancements in fields such as industrial processes, environmental science, and even astrophysics.
Moreover, modern technology and scientific advancements have enabled experimental verification and validation of the predicted speeds of gas molecules. Sophisticated instruments and computational simulations allow scientists to observe and measure the velocities of gas molecules, confirming the theoretical predictions derived from the kinetic theory.
The concept of the most probable speed of gas molecules, as elucidated by the kinetic theory, offers a key insight into the dynamic nature of gas behavior. Understanding this fundamental aspect not only contributes to scientific knowledge but also finds practical applications in diverse domains, shaping our comprehension and utilization of gases in our everyday lives and beyond.
Join Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your chemistry knowledge. and build a strong foundation.
| Related Links | |
| Potassium Fluoride Formula | Potassium Chlorate Formula |
| Potassium Bromate Formula | Gold Formula |
Most Probable Speed of Gas Molecules FAQs
What is the most probable speed of gas molecules?
How is the most probable speed determined?
What factors influence the most probable speed?
Why is the most probable speed important?










