
NCERT Solutions for Class 12 Maths Chapter 10
NCERT Solutions for Class 12 Maths Chapter 10: It’ll be helpful for students to refer to the Vector Algebra Class 12 solutions given here. Studying Vector Algebra becomes much easier if students refer to the solutions given here. This lesson helps one comprehend how scalar and vector quantities differ, what their properties are, vector operations, etc. This chapter is crucial to students scoring high marks in the board exams and doing well in competitive exams. The NCERT Solutions for Class 12 Maths Chapter 10 put students in good stead for facing the challenge of the board exams of Class 12. The solutions for Maths Class 12 Chapter 10 Vector Algebra given here are easy for students to understand, even the weaker ones. There’s no skipping of steps in any of the solutions given below which makes sure that students have a clear understanding of all the concepts of Vector Algebra Class 12 . Written as per the current CBSE syllabus 2023-24, the solutions below shall greatly help studentsto feel confident about facing the Class 12 board exams. Students can also download the PDF file for reference offline.NCERT Solutions for Class 12 Maths Chapter 10 Overview
This article intends to help students form a clear understanding of the concepts of Maths Class 12 Chapter 10 Vector Algebra . The solutions are given from the students’ perspective which has made them easy to understand. The discussion below includes the major concepts of Vector Algebra that many students otherwise find confusing. The solutions are so prepared, they help students understand the basics of Vector Algebra which is the difference between scalar and vector quantities. Our NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra solutions make the concepts of the subject clear to the students helping them remove any ambiguity they may have. The Class 12 Maths Chapter 10 Vector Algebra solutions , here give a clear explanation of the various concepts included in Vector Algebra. Many students find the subject a tough hurdle to overcome. Our experts have taken care to see things the way students do and hence kept the explanations very simple.NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra
Exercise 10.1 Page No: 428 1. Represent graphically a displacement of 40 km, 30° east of north. Solution: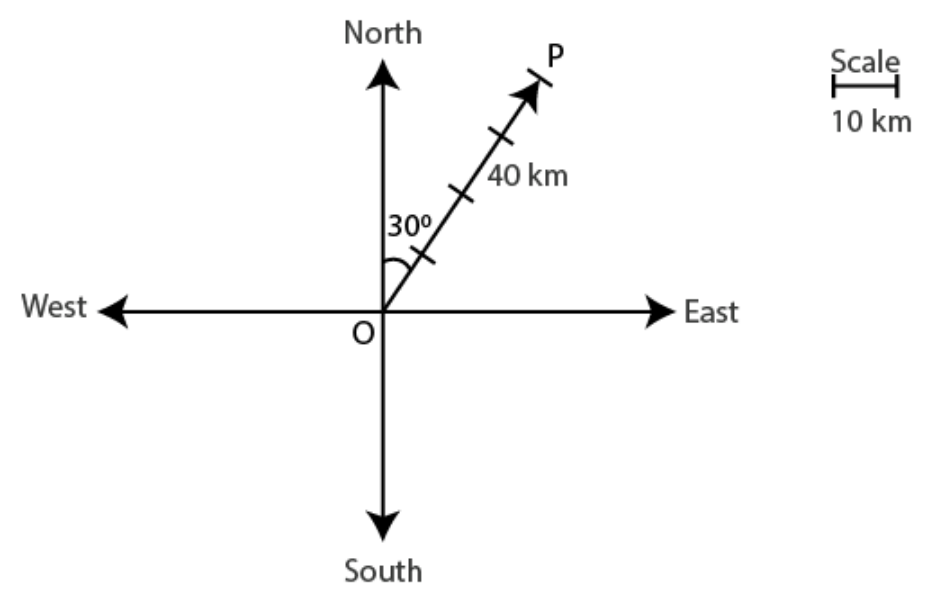 The vector OP
represents the displacement of 40 km, 30
o
east of north.
2. Classify the following measures as scalars and vectors.
(i) 10 kg (ii) 2 metres north-west (iii) 40°
(iv) 40 watt (v) 10
–19
coulomb (vi) 20 m/s
2
Solution:
(i)
10 kg is a scalar quantity because it has only magnitude.
(ii)
2 meters north-west is a vector quantity as it has both magnitude and direction.
(iii)
40° is a scalar quantity as it has only magnitude.
(iv)
40 watt is a scalar quantity as it has only magnitude.
(v)
10
–19
coulomb is a scalar quantity as it has only magnitude.
(vi)
20 m/s
2
is a vector quantity as it has both magnitude and direction.
3. Classify the following as scalar and vector quantities.
(i) time period (ii) distance (iii) force
(iv) velocity (v) work done
Solution:
(i)
Time period is a scalar quantity as it has only magnitude.
(ii)
Distance is a scalar quantity as it has only magnitude.
(iii)
Force is a vector quantity as it has both magnitude and direction.
(iv)
Velocity is a vector quantity as it has both magnitude as well as direction.
(v)
Work done is a scalar quantity as it has only magnitude.
4. In Figure, identify the following vectors.
The vector OP
represents the displacement of 40 km, 30
o
east of north.
2. Classify the following measures as scalars and vectors.
(i) 10 kg (ii) 2 metres north-west (iii) 40°
(iv) 40 watt (v) 10
–19
coulomb (vi) 20 m/s
2
Solution:
(i)
10 kg is a scalar quantity because it has only magnitude.
(ii)
2 meters north-west is a vector quantity as it has both magnitude and direction.
(iii)
40° is a scalar quantity as it has only magnitude.
(iv)
40 watt is a scalar quantity as it has only magnitude.
(v)
10
–19
coulomb is a scalar quantity as it has only magnitude.
(vi)
20 m/s
2
is a vector quantity as it has both magnitude and direction.
3. Classify the following as scalar and vector quantities.
(i) time period (ii) distance (iii) force
(iv) velocity (v) work done
Solution:
(i)
Time period is a scalar quantity as it has only magnitude.
(ii)
Distance is a scalar quantity as it has only magnitude.
(iii)
Force is a vector quantity as it has both magnitude and direction.
(iv)
Velocity is a vector quantity as it has both magnitude as well as direction.
(v)
Work done is a scalar quantity as it has only magnitude.
4. In Figure, identify the following vectors.
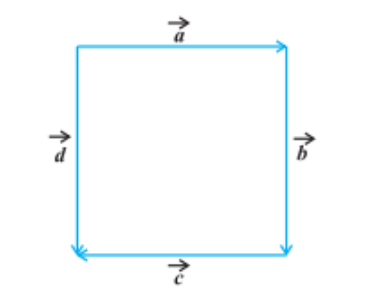 (i) Coinitial (ii) Equal (iii) Collinear but not equal
Solution:
(i) Coinitial (ii) Equal (iii) Collinear but not equal
Solution:
 directions are not the same.
directions are not the same.
Exercise 10.2 Page No: 440
1. Compute the magnitude of the following vectors.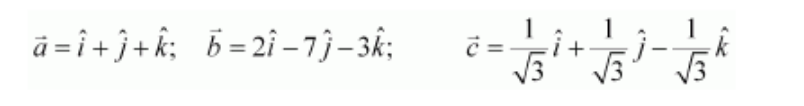 Solution:
Given, vectors are
Solution:
Given, vectors are
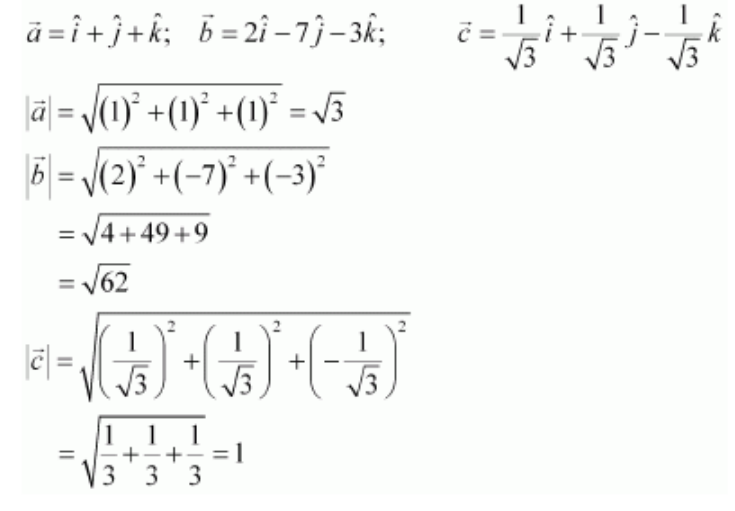 2. Write two different vectors having the same magnitude.
Solution:
2. Write two different vectors having the same magnitude.
Solution:
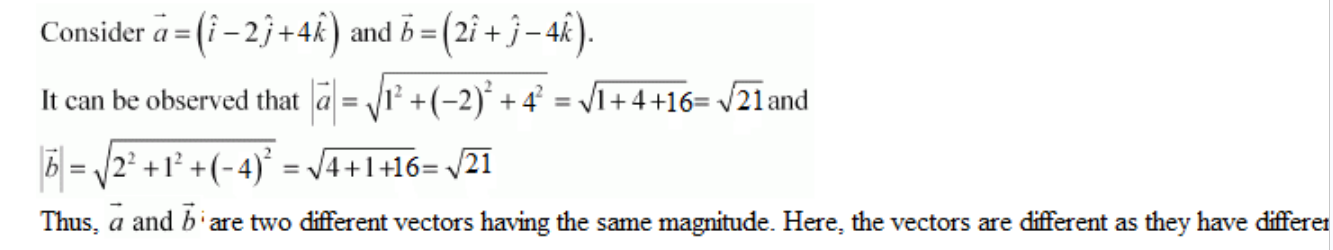 3. Write two different vectors having the same direction.
Solution:
Two different vectors having the same directions are
Let us
3. Write two different vectors having the same direction.
Solution:
Two different vectors having the same directions are
Let us
 4. Find the values of
x
and
y
so that the vectors
4. Find the values of
x
and
y
so that the vectors
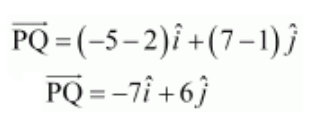
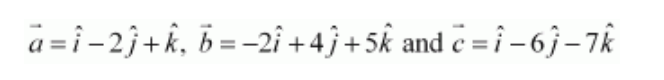 6. Find the sum of the vectors.
Solution:
Let us find the sum of the vectors.
6. Find the sum of the vectors.
Solution:
Let us find the sum of the vectors.
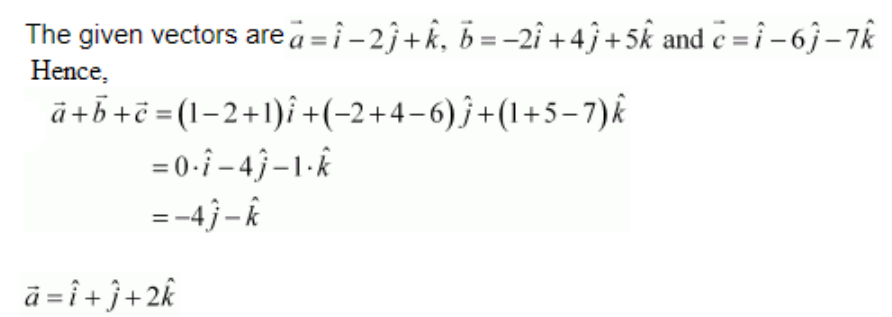 7. Find the unit vector in the direction of the vector.
Solution:
We know that
7. Find the unit vector in the direction of the vector.
Solution:
We know that
 8. Find the unit vector in the direction of vector, where P and Q are the points
(1, 2, 3) and (4, 5, 6), respectively.
Solution:
We know that,
8. Find the unit vector in the direction of vector, where P and Q are the points
(1, 2, 3) and (4, 5, 6), respectively.
Solution:
We know that,
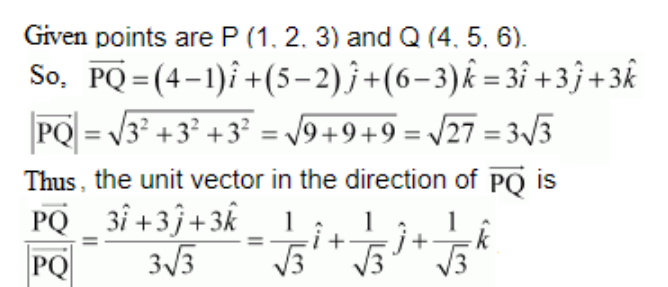
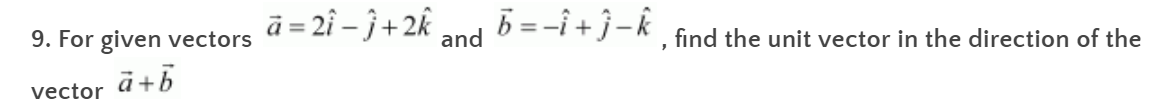 Solution:
We know that,
Solution:
We know that,

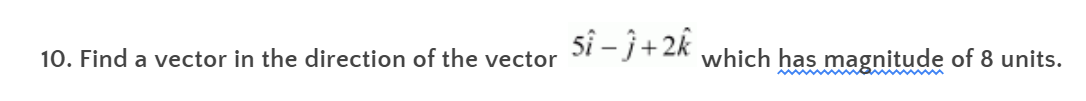 Solution:
Firstly,
Solution:
Firstly,
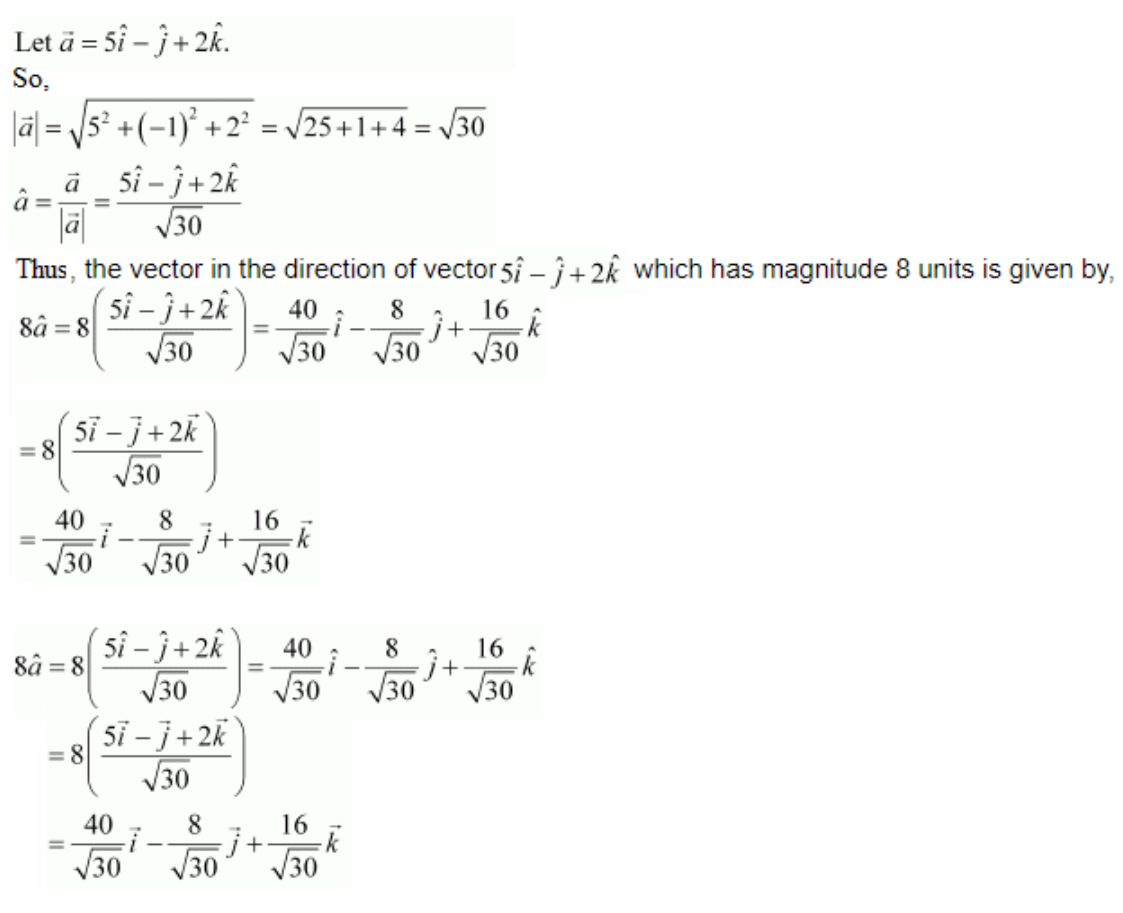
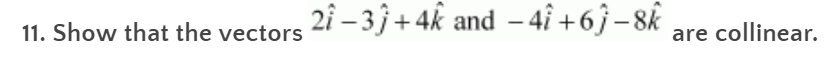 Solution:
First,
Solution:
First,
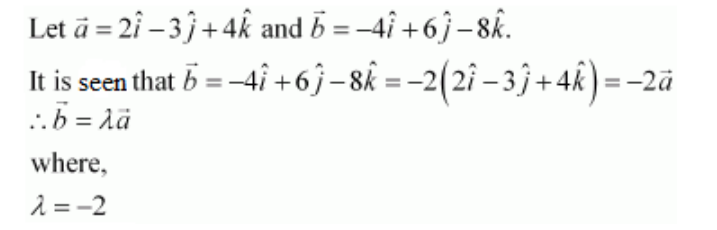 Therefore, we can say that the given vectors are collinear.
Therefore, we can say that the given vectors are collinear.
 Solution:
First,
Solution:
First,
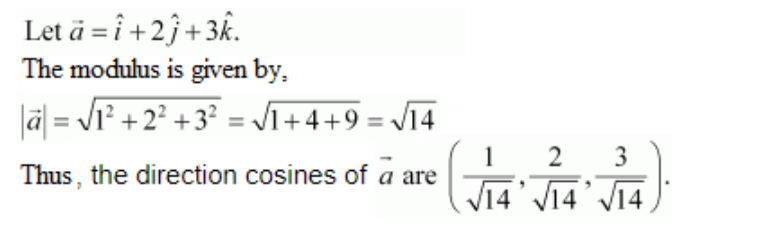 13. Find the direction cosines of the vector joining the points A (1, 2, –3) and
B (–1, –2, 1) directed from A to B.
Solution:
We know that the given points are A (1, 2, –3) and B (–1, –2, 1).
Now,
13. Find the direction cosines of the vector joining the points A (1, 2, –3) and
B (–1, –2, 1) directed from A to B.
Solution:
We know that the given points are A (1, 2, –3) and B (–1, –2, 1).
Now,
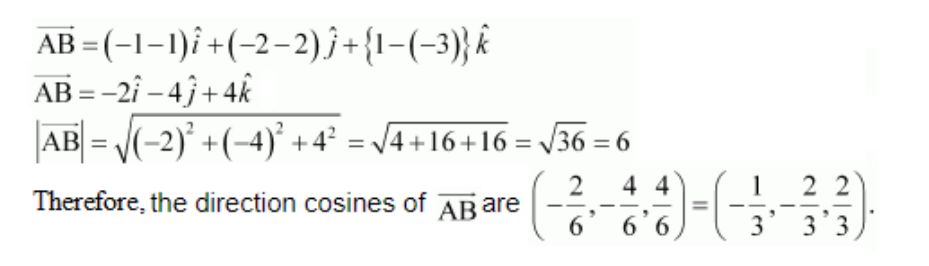
 Solution:
Firstly,
Solution:
Firstly,
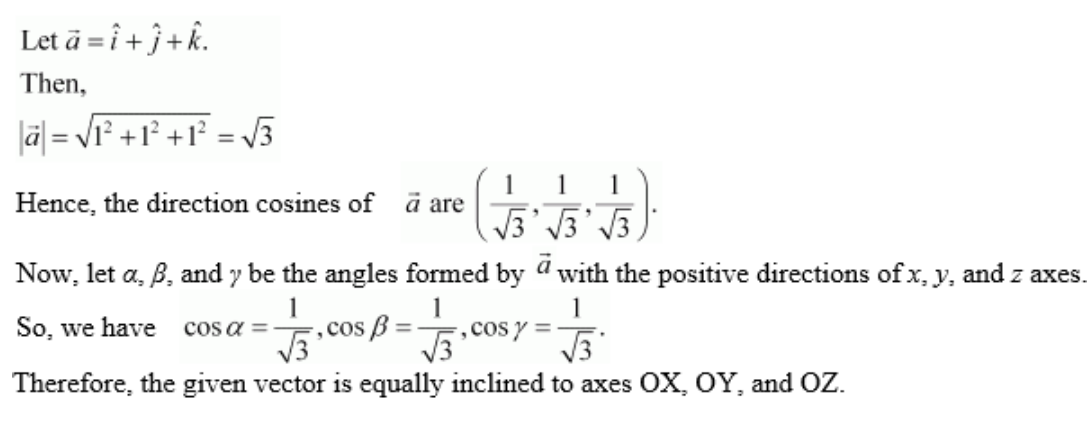 16. Find the position vector of the midpoint of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Solution:
The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by
16. Find the position vector of the midpoint of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Solution:
The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by
 Solution:
We know
Given position vectors of points A, B, and C are
Solution:
We know
Given position vectors of points A, B, and C are
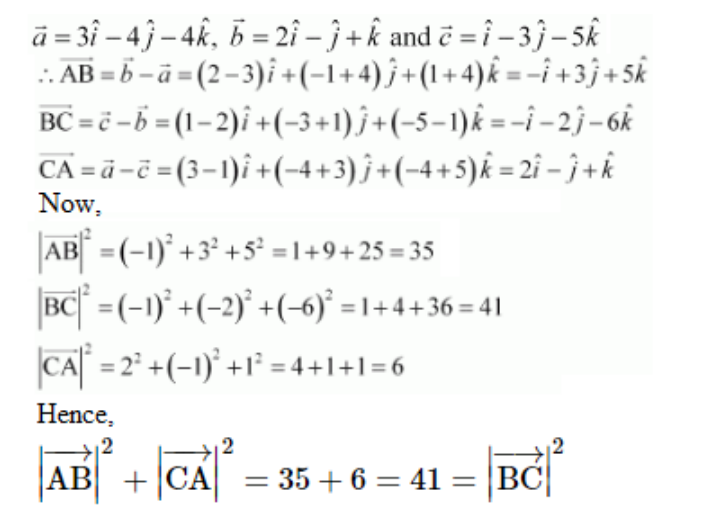 Hence, proved that the given points form the vertices of a right-angled triangle.
18. In triangle ABC (Fig 10.18), which of the following is not true.
Hence, proved that the given points form the vertices of a right-angled triangle.
18. In triangle ABC (Fig 10.18), which of the following is not true.
 Solution:
First, let us consider,
Solution:
First, let us consider,

Exercise 10.3 Page No: 447
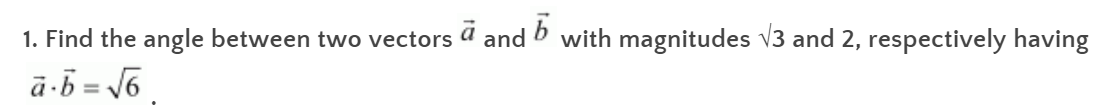 Solution:
First, let us consider,
Solution:
First, let us consider,
 2. Find the angle between the vectors
2. Find the angle between the vectors
 Hence, the angle between the vectors is cos
-1
(5/7).
Hence, the angle between the vectors is cos
-1
(5/7).
 Solution:
First,
Solution:
First,

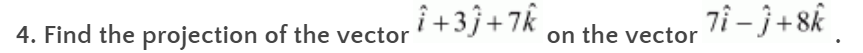 Solution:
First,
Solution:
First,
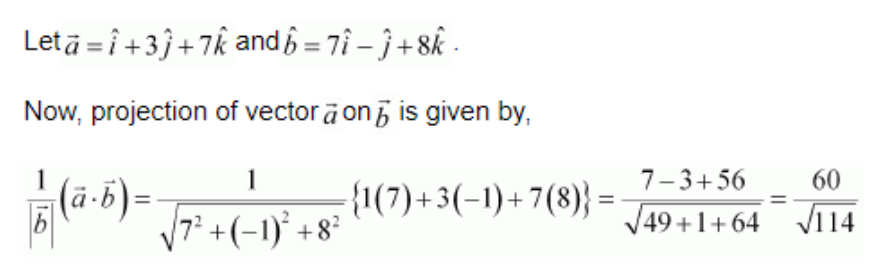 Hence, the projection is 60/
√
114.
5. Show that each of the given three vectors is a unit vector.
Hence, the projection is 60/
√
114.
5. Show that each of the given three vectors is a unit vector.
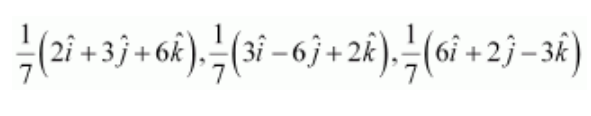 Also, show that they are mutually perpendicular to each other.
Solution:
It is given that
Also, show that they are mutually perpendicular to each other.
Solution:
It is given that

 6. Find
Solution:
Let us consider,
6. Find
Solution:
Let us consider,
 7. Evaluate the product
7. Evaluate the product
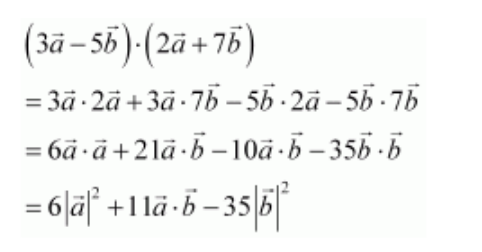 8. Find the magnitude of two vectors
8. Find the magnitude of two vectors
 Hence, the magnitude of the two vectors is 1.
Hence, the magnitude of the two vectors is 1.
 Solution:
Let us consider,
Solution:
Let us consider,
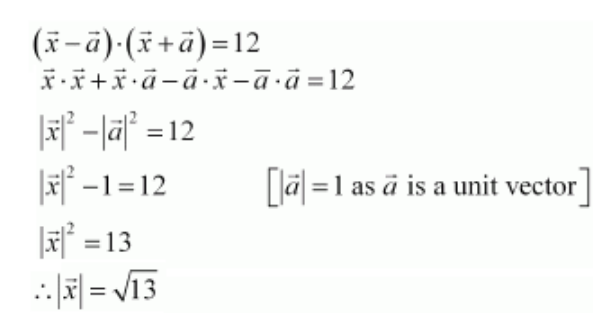 Hence, the value is
√
13.
Hence, the value is
√
13.
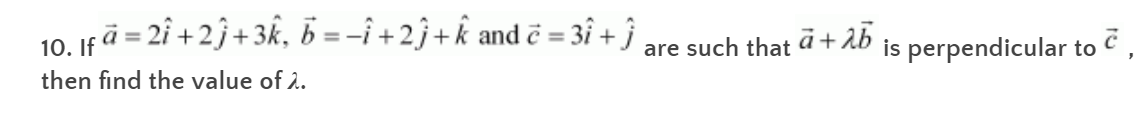 Solution:
We know that the
Solution:
We know that the

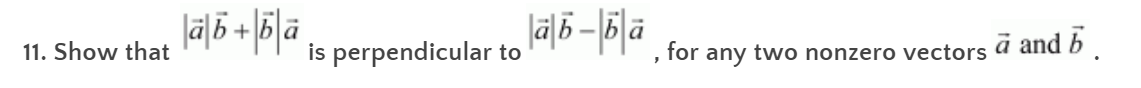 Solution:
Let us consider,
Solution:
Let us consider,
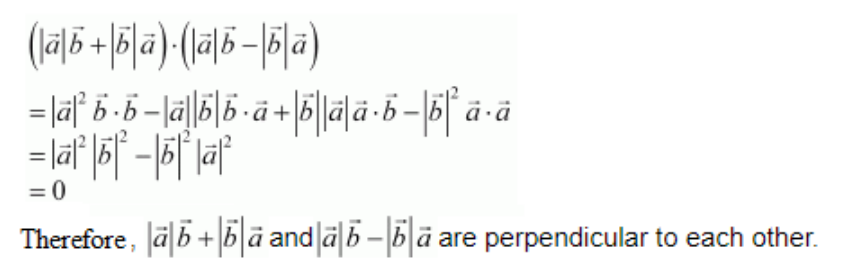
 Solution:
Consider the given vectors,
Solution:
Consider the given vectors,
 Hence, the value is -3/2.
Hence, the value is -3/2.
 Solution:
First,
Solution:
First,
 Solution:
We know,
Solution:
We know,
 Hence, the angle is cos
-1
(10/
√
102).
16. Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Solution:
Let us consider,
Given points are A (1, 2, 7), B (2, 6, 3), and C (3, 10, –1).
Now,
Hence, the angle is cos
-1
(10/
√
102).
16. Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Solution:
Let us consider,
Given points are A (1, 2, 7), B (2, 6, 3), and C (3, 10, –1).
Now,
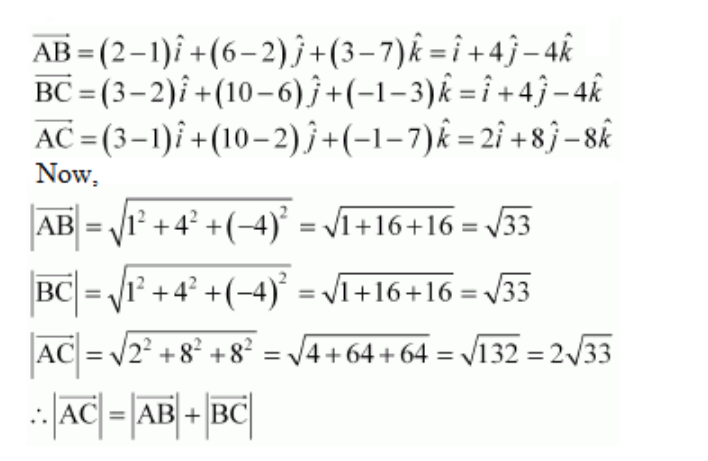 Therefore, the given points A, B, and C are collinear.
Therefore, the given points A, B, and C are collinear.
 Solution:
First, consider
Solution:
First, consider

 Solution:
Explanation:
Solution:
Explanation:

NCERT Solutions for Class 12 Maths Chapter 10 - Topics Included
The lesson here includes the concepts covered in Chapter 10 of Class 12 as laid out by NCERT. The details are given below.10.1 Introduction
10.2 Basic Concepts
- Position Vector
- Direction Cosines
10.3 Types of Vectors
- Zero Vector
- Unit Vector
- Coinitial Vectors
- Collinear Vectors
- Equal Vectors
- Negative of a Vector
10.4 Addition of Vectors
10.5 Multiplication of a Vector by a Scalar
10.5.1 Components of a vector
10.5.2 Vector joining two points
10.5.3 Section formula
10.6 Product of Two Vectors
10.6.1 Scalar (or dot) product of two vectors
10.6.2 Projection of a vector on a line
10.6.3 Vector (or cross) product of two vectors
NCERT Solutions for Class 12 Maths Chapter 10 – Vector Algebra
The Vector Algebra chapter is a part of the Unit Vectors and Three-Dimensional Geometry which carry 14 marks of the total. This chapter also includes a miscellaneous exercise apart from 4 exercises. It goes a long way in helping students form a clear understanding of Vector Algebra and Vectors. We have mentioned some of the major topics covered in Chapter 10 of Vector Algebra Class 12 .- The scalar components of a vector are its direction ratios and represent its projections along the respective axes.
- The magnitude (r), direction ratios (a, b, c) and direction cosines (l, m, n) of any vector are related as l=(a/r), m=(b/r) n=(c/r)
- The vector sum of the three sides of a triangle taken in order is 0.
- The vector sum of two coinitial vectors is given by the diagonal of the parallelogram whose adjacent sides are the given vectors.
- The multiplication of a given vector by a scalar λ changes the magnitude of the vector by the multiple |λ| and keeps the direction the same (or makes it opposite) accordingly, as the value of λ is positive (or negative).
NCERT Solutions for Class 12 Maths Chapter 10 Vector Algebra- Key Features
Students can refer to the solutions for Vector Algebra Class 12 which shall enable them to understand the following clearly.- Vectors and scalars,
- Magnitude and direction of a vector.
- Direction cosines and direction ratios of a vector.
- Types of vectors (equal, unit, zero, parallel and collinear vectors),
- position vector of a point, negative of a vector,
- components of a vector,
- the addition of vectors,
- multiplication of a vector by a scalar,
- Position vector of a point dividing a line segment in a given ratio.
- Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors,
- vector (cross) product of vectors,
- The scalar triple product of vectors.
NCERT Solutions for Class 12 Maths Chapter 10 FAQs
What do students learn from the Class 12 Maths Chapter 10 Vector Algebra solutions?
Students get to learn about how scalar and vector quantities differ, what their properties are, vector operations and other concepts. With a clear understanding of these concepts, the students can handle the chapter on Vector Algebra with ease.
What’s an effective strategy to learn Vector Algebra well?
Going through the chapter helps a great deal. Apart from that, regular practice is a must. Refer to the Vector Algebra Class 12 solutions here to form a clear understanding of the major concepts. There’s no substitute to regular practice. Do so diligently.
Do my chances of doing well in the exams rise if I refer to the solutions here?
Our experts have prepared theMaths class 12 chapter 10 Vector Algebra solutionstaking care to see that no step is skipped. That helps explain all the concepts clearly. Detailed explanations help form a deep understanding of the subject and do well in the exams.
Do the solutions really help students get better at dealing with Maths?
Our team of experts has prepared the solutions to Vector Algebra Class 12 from the students’ perspective. The team has put itself in the students’ shoes and that has helped them gauge what challenges students face. It has helped the team prepare the answers more effectively.
Will the solutions here help score better in the exams?
We need to get to the root of the problem. Students suffer when their base in Maths is weak. Hence, the process of teaching Maths in easy to understand methods should begin in the lower classes itself. Keeping this in mind, we have kept our approach to Vector Algebra Class 12 very simple. Not a single step has been skipped in the solutions. Such detailed answers shall surely help score better in the exams. A thorough and systematic answer does indeed raise the chances of scoring higher in the exams.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.









