
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise (Vector Algebra)
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise Vector Algebra is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of Chapter 10. Given below are step-by-step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise.NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.1
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise Overview
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Excercise addresses these significant subjects. In order to fully comprehend the concepts presented in the chapter and make effective use of the provided solutions, it is recommended that students go over each topic in great detail. The intention is for students to effortlessly achieve excellent exam scores after reviewing and practicing these responses.NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise:
Question 1. Write down a unit vector in XY-plane making an angle of 30° with the positive direction of x-axis. Solution : If is a unit vector in the XY-plane, then
is a unit vector in the XY-plane, then
 Here,
θ
is the angle made by the unit vector with the positive direction of the
x
-axis.
Therefore, for
θ
= 30°:
Here,
θ
is the angle made by the unit vector with the positive direction of the
x
-axis.
Therefore, for
θ
= 30°:
 Question
2. Find the scalar components and magnitude of the vector joining the points
Question
2. Find the scalar components and magnitude of the vector joining the points
 Solution :
Given points are
Solution :
Given points are

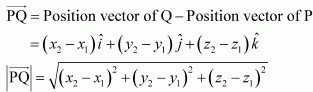 Hence, the scalar components and the magnitude of the vector joining the given points are respectively
Hence, the scalar components and the magnitude of the vector joining the given points are respectively

NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.2
Question 3. A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure. Solution : Let O and B be the initial and final positions of the girl respectively. Then, the girl’s position can be shown as: Hence, the girl’s displacement from her initial point of departure is
Hence, the girl’s displacement from her initial point of departure is

 Question 4. If
Question 4. If
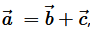 then is it true that
then is it true that
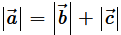 Justify your answer.
Solution :
Justify your answer.
Solution :

NCERT Solutions for Class 12 Maths Chapter 10 Exercise 10.3
Question 5. Find the value of x for which x (.png) ) is a unit vector.
Solution :
x (
) is a unit vector.
Solution :
x (
.png) )
is a unit vector if |
x (
)
is a unit vector if |
x (
.png) )| = 1
)| = 1
 Hence, the required value of
x
is ± 1/√3.
Question 6. Find a vector of magnitude 5 units and parallel to the resultant of the vectors
Hence, the required value of
x
is ± 1/√3.
Question 6. Find a vector of magnitude 5 units and parallel to the resultant of the vectors
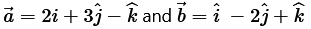 Solution :
Given: Vectors
Solution :
Given: Vectors
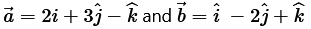 Let
Let
.png) be the resultant of
be the resultant of
.png) and
and
.png)
 Hence, the vector of magnitude 5 units and parallel to the resultant of vectors
Hence, the vector of magnitude 5 units and parallel to the resultant of vectors
.png) and
and
.png) is
is
 Question 7. If
Question 7. If
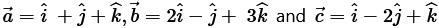 find a unit vector parallel to the vector
find a unit vector parallel to the vector
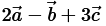 Solution :
Given: Vectors
Solution :
Given: Vectors
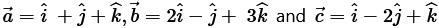
 Question 8. Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear and find the ratio in which B divides AC.
Solution :
The given points are A (1, –2, –8), B (5, 0, –2), and C (11, 3, 7).
Question 8. Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear and find the ratio in which B divides AC.
Solution :
The given points are A (1, –2, –8), B (5, 0, –2), and C (11, 3, 7).
 Hence, point B divides AC in the ratio 2 : 3.
Hence, point B divides AC in the ratio 2 : 3.
Question 9. Find the position vector of a point R which divides the line joining the two points P and Q whose position vectors are (2
.png) +
+
.png) ) and (
) and (
.png) - 3
- 3
.png) ) externally in the ratio 1 : 2. Also, show that P is the middle point of line segment RQ.
) externally in the ratio 1 : 2. Also, show that P is the middle point of line segment RQ.
 .
It is given that point R divides a line segment joining two points P and Q externally in the ratio 1: 2. Then, on using the section formula, we get:
.
It is given that point R divides a line segment joining two points P and Q externally in the ratio 1: 2. Then, on using the section formula, we get:
 Therefore, the position vector of point R is
Therefore, the position vector of point R is
 .
Position vector of the mid-point of RQ =
.
Position vector of the mid-point of RQ =

 Hence, P is the mid-point of the line segment RQ.
Question 10. Two adjacent sides of a parallelogram are
Hence, P is the mid-point of the line segment RQ.
Question 10. Two adjacent sides of a parallelogram are
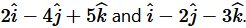 Find the unit vector parallel to its diagonal. Also, find its area.
Solution :
Adjacent sides of a parallelogram are given as:
Find the unit vector parallel to its diagonal. Also, find its area.
Solution :
Adjacent sides of a parallelogram are given as:
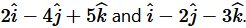 Then, the diagonal of a parallelogram is given by
Then, the diagonal of a parallelogram is given by
.png) +
+
.png) .
.
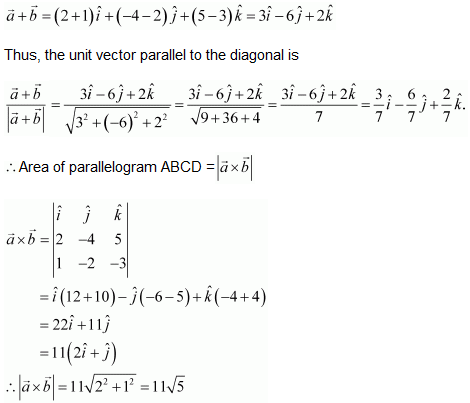 Hence, the area of the parallelogram is 11√5 square units.
Question 11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are
Hence, the area of the parallelogram is 11√5 square units.
Question 11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are
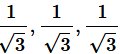 Solution :
Let a vector be equally inclined to axes OX, OY, and OZ at angle
α
.
Then, the direction cosines of the vector are cos
α
, cos
α
, and cos
α
.
Solution :
Let a vector be equally inclined to axes OX, OY, and OZ at angle
α
.
Then, the direction cosines of the vector are cos
α
, cos
α
, and cos
α
.
 Hence, the direction cosines of the vector which are equally inclined to the axes are
Hence, the direction cosines of the vector which are equally inclined to the axes are
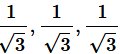 .
Question 12. Let
.
Question 12. Let
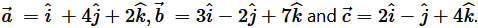 Find a vector
Find a vector
.png) which is perpendicular to both
which is perpendicular to both
.png) and
and
.png) and
and
.png) .
.
.png) = 15
Solution :
= 15
Solution :
 Question 13. The scalar product of the vector
Question 13. The scalar product of the vector
.png) with a unit vector along the sum of vectors
with a unit vector along the sum of vectors
 is equal to one. Find the value of λ.
Solution :
is equal to one. Find the value of λ.
Solution :
 Hence, the value of
λ
is 1.
Question 14. If are mutually perpendicular vectors of equal magnitudes, show that the vector
Hence, the value of
λ
is 1.
Question 14. If are mutually perpendicular vectors of equal magnitudes, show that the vector
.png) +
+
.png) +
+
.png) is equally inclined to
is equally inclined to
.png) ,
,
.png) , and
, and
.png) .
Solution :
Since
.
Solution :
Since
.png) ,
,
.png) , and
, and
.png) are mutually perpendicular vectors, we have
are mutually perpendicular vectors, we have
.png) .
.
.png) =
=
.png) .
.
.png) =
=
.png) .
.
.png) = 0
It is given that:
|
= 0
It is given that:
|
.png) | = |
| = |
.png) | = |
| = |
.png) |
Let vector
|
Let vector
.png) +
+
.png) +
+
.png) be inclined to
be inclined to
.png) ,
,
.png) ,
and
,
and
.png) at angles θ
1
,θ
2
and θ
3
respectively.
Then, we have:
at angles θ
1
,θ
2
and θ
3
respectively.
Then, we have:
 Hence, the vector (
Hence, the vector (
.png) +
+
.png) +
+
.png) )
is equally inclined to
)
is equally inclined to
.png) ,
,
.png) ,
and
,
and
.png) .
Question 15. Prove that
.
Question 15. Prove that
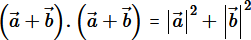 if and only if
if and only if
.png) ,
,
.png) are perpendicular given
are perpendicular given
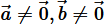 .
Solution :
.
Solution :
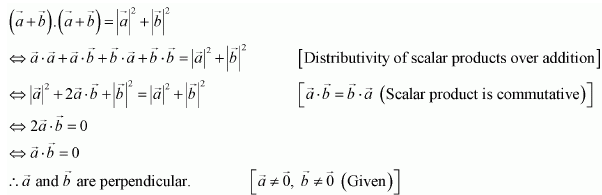 Question 16. Choose the correct answer:
If
θ
is the angle between two vectors
Question 16. Choose the correct answer:
If
θ
is the angle between two vectors
.png) and
and
.png) then
then
.png) .
.
.png) ≥0
only when:
≥0
only when:
 Solution :
Let
θ
be the angle between two vectors
Solution :
Let
θ
be the angle between two vectors
.png) and
and
.png) .
Then, without loss of generality,
.
Then, without loss of generality,
.png) and
and
.png) are non-zero vectors so that |
are non-zero vectors so that |
.png) | and |
| and |
.png) | are positives
It is known that
| are positives
It is known that
.png) ..
..
.png) = |
= |
.png) ||
||
.png) |cosθ
|cosθ
 Therefore, option (B) is correct.
Question 17. Choose the correct answer:
Let
Therefore, option (B) is correct.
Question 17. Choose the correct answer:
Let
.png) and
and
.png) be two unit vectors and
θ
is the angle between them. Then
be two unit vectors and
θ
is the angle between them. Then
.png) +
+
.png) is a unit vector if
(A) θ = π/4
(B) θ = π/3
(C) θ = π/2
(D) θ = π/3
Solution :
Let
is a unit vector if
(A) θ = π/4
(B) θ = π/3
(C) θ = π/2
(D) θ = π/3
Solution :
Let
.png) and
and
.png) be two unit vectors and
θ
be the angle between them.
Then, |
be two unit vectors and
θ
be the angle between them.
Then, |
.png) | = |
| = |
.png) | = 1
Now,
| = 1
Now,
.png) +
+
.png) is a unit vector if |
is a unit vector if |
.png) +
+
.png) | = 1
| = 1
 Hence,
Hence,
.png) +
+
.png) is a unit vector if θ = 2π/3.
Therefore, option (D) is correct.
Question 18. Choose the correct answer:
The value of
is a unit vector if θ = 2π/3.
Therefore, option (D) is correct.
Question 18. Choose the correct answer:
The value of
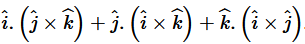 is:
(A) 0
(B) -1
(C) 1
(D) 3
Solution :
is:
(A) 0
(B) -1
(C) 1
(D) 3
Solution :
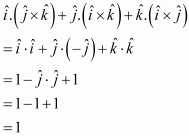 Therefore, option (C) is correct.
Question 19. If θ be the angle between any two vectors
Therefore, option (C) is correct.
Question 19. If θ be the angle between any two vectors
.png) and
and
.png) , then
, then
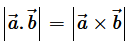 when
θ is equal to:
(A) 0
(B) π/4
(C) π/2
(D) π
Solution :
Let
θ
be the angle between two vectors
when
θ is equal to:
(A) 0
(B) π/4
(C) π/2
(D) π
Solution :
Let
θ
be the angle between two vectors
.png) and
and
.png) .
Then, without loss of generality,
.
Then, without loss of generality,
.png) and
and
.png) are non-zero vectors, so that
|
are non-zero vectors, so that
|
.png) | and |
| and |
.png) | are positive.
| are positive.
 Therefore, option (B) is correct.
Therefore, option (B) is correct.
NCERT Solutions for Class 12 Maths Chapter 10 Miscellaneous Exercise FAQs
What is the hardest chapter in 12 Maths?
For most of the students, the hardest chapter is integrals.
How many exercises are there in Chapter 10 Maths class 12?
NCERT Solutions Class 12 Maths Chapter 10 Vector Algebra has a total of 63 questions that have been spread across 5 exercises including a miscellaneous one.
Which is the most important chapter in Maths class 12?
Students must give priority to those chapters primarily that consist of major weightage of marks. Algebra, Calculus, Vectors, and Three-Dimensional Geometry are the most vital chapters from this perspective.
What is a collinear vector?
Vectors that lie along the same line or parallel lines are known to be collinear vectors. They are also known as parallel vectors. Two vectors are collinear if they are parallel to the same line irrespective of their magnitudes and direction.
What is a vector in 12th maths?
Vector Algebra for class 12 is all about the study of vectors and scalars. There are various quantities, which involves magnitude as well as direction. If the quantity that has magnitude, as well as direction, is known as vectors. Such quantities are known as Vector Quantities.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App










