NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming
NCERT Solutions for Class 12 Maths Chapter 12 are a detailed explanation of the problems the chapter includes. Physics Wallah experts have come up with simply laid out solutions that shall help students of Class 12 CBSE understand mathematical concepts. The article here is intended to be a ready reference for students that shall help them understand Linear Programming.
Jasdeep Bhatia25 Jan, 2024
Share
NCERT Solutions for Class 12 Maths Chapter 12
NCERT Solutions for Class 12 Maths Chapter 12 : The solutions given here help form a clear understanding of Linear Programming Class 12 . As a helpful reference tool, the article makes it easier for students to grasp the concepts of Linear Programming. The best method that can be used for achieving the best outcome in a mathematical model where linear relationships explain represent the requirements is called Linear Programming. This article helps students learn the fundamentals of Linear Programming much better. Repeated practice of the solutions given here by Physics Wallah experts help students ace the board exams. This article’s Maths Class 12 Chapter 12 Linear Programming solutions are given in easy to understand steps that help form a clear concept of Linear Programming. The Physics Wallah experts have taken care to see to it that the simplest methods are used in explaining the problems. As such, this article shall be of great help to even the weaker students of Linear Programming. Linear Programming Class 12 becomes a much easier challenge to face with our Class 12 Maths Chapter 12 Linear Programming solutions . The solutions are in accordance with the Class 12 CBSE syllabus. Physics Wallah also gives students the option to download the PDF file free so they can refer to it offline whenever they study.NCERT Solutions for Class 12 Maths Chapter 12 Overview
The experts at Physics Wallah seek to help students clarify their doubts about Linear Programming Class 12 with the solutions that this article contains. The experts have put themselves in the weaker students’ shoes and that has helped keep the solutions very simple. The methods used to solve the problems are indeed very easy to understand. The Class 12 Maths Chapter 12 Linear Programming solutions Class 12 Maths Chapter 12 Linear Programming solutions given here help students overcome their doubts about Linear Programming. Students can always refer to this article, available both online and offline and practice regularly so that they can improve their skills at solving Linear Programming problems. The Linear Programming Class 12 solutions from Physics Wallah help students a lot when it comes to forming a clear and thorough understanding of the subject. Students have for long found this chapter confusing. The easy solutions given in this article help even the weaker students understand Linear Programming deeply since every aspect is discussed in details.NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming
Exercise 12.1 Page No. 513 1. Maximise Z = 3 x + 4 y Subject to the constraints: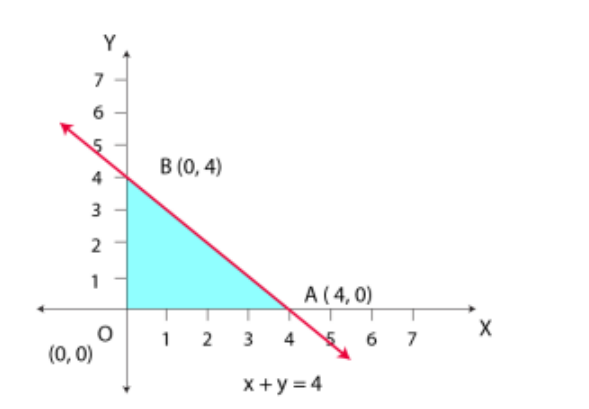
Solution:
The feasible region determined by the constraints, x + y ≤ 4, x ≥ 0, y ≥ 0, is given below.
O (0, 0), A (4, 0), and B (0, 4) are the corner points of the feasible region. The values of Z at these points are given below.
| Corner point | Z = 3x + 4y | |
| O (0, 0) | 0 | |
| A (4, 0) | 12 | |
| B (0, 4) | 16 | Maximum |
The feasible region determined by the system of constraints,
given below.
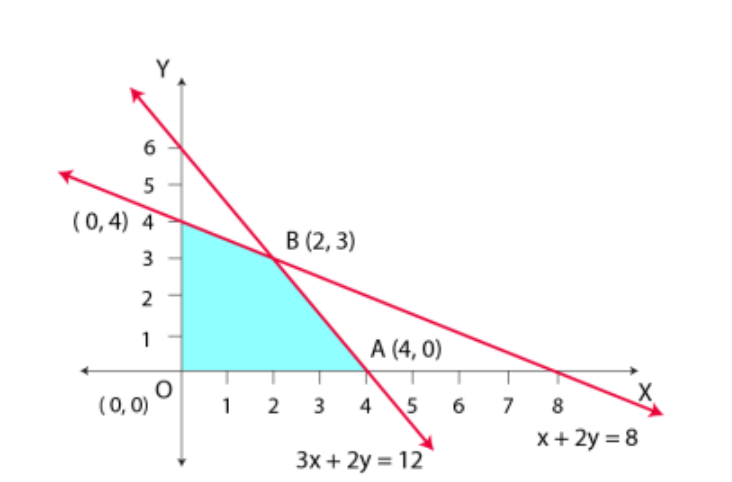O (0, 0), A (4, 0), B (2, 3) and C (0, 4) are the corner points of the feasible region.
The values of Z at these corner points are given below.
| Corner point | Z = – 3x + 4y | |
| O (0, 0) | 0 | |
| A (4, 0) | -12 | Minimum |
| B (2, 3) | 6 | |
| C (0, 4) | 16 |
Solution:
The feasible region determined by the system of constraints, 3
x
+ 5
y
≤ 15, 5
x
+ 2
y
≤ 10,
x
≥ 0, and
y
≥ 0, is given below.
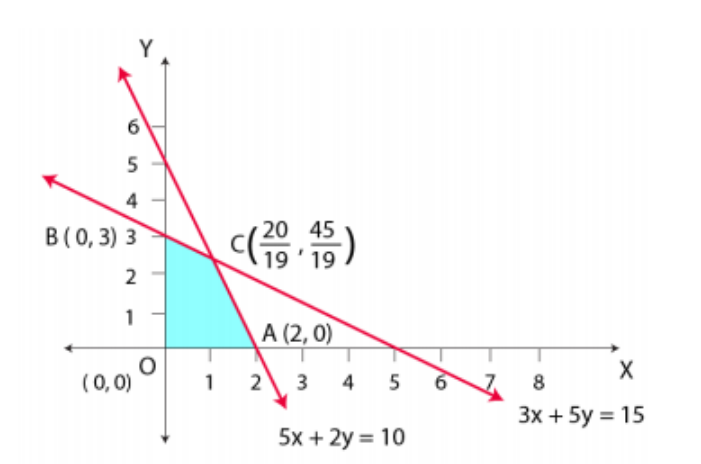O (0, 0), A (2, 0), B (0, 3) and C (20 / 19, 45 / 19) are the corner points of the feasible region. The values of Z at these corner points are given below.
| Corner point | Z = 5x + 3y | |
| O (0, 0) | 0 | |
| A (2, 0) | 10 | |
| B (0, 3) | 9 | |
| C (20 / 19, 45 / 19) | 235 / 19 | Maximum |
Solution:
The feasible region determined by the system of constraints, x + 3y ≥ 3, x + y ≥ 2, and x, y ≥ 0, is given below.
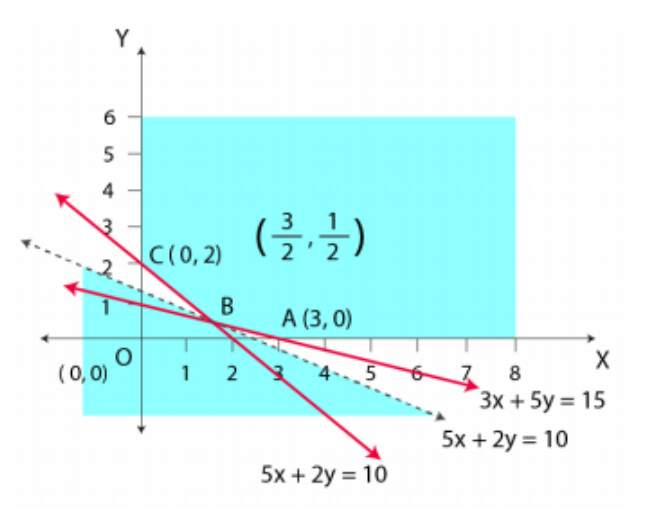It can be seen that the feasible region is unbounded.
The corner points of the feasible region are A (3, 0), B (3 / 2, 1 / 2) and C (0, 2).
The values of Z at these corner points are given below.
| Corner point | Z = 3x + 5y | |
| A (3, 0) | 9 | |
| B (3 / 2, 1 / 2) | 7 | Smallest |
| C (0, 2) | 10 |
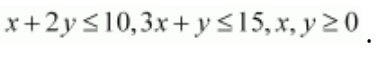Solution:
The feasible region determined by the constraints,
x
+ 2
y
≤ 10, 3
x
+
y
≤ 15,
x
≥ 0, and
y
≥ 0, is given below.
A (5, 0), B (4, 3), C (0, 5) and D (0, 0) are the corner points of the feasible region.
The values of Z at these corner points are given below.
| Corner point | Z = 3x + 2y | |
| A (5, 0) | 15 | |
| B (4, 3) | 18 | Maximum |
| C (0, 5) | 10 |
Solution:
The feasible region determined by the constraints, 2
x
+
y
≥ 3,
x
+ 2
y
≥ 6,
x
≥ 0, and
y
≥ 0, is given below.
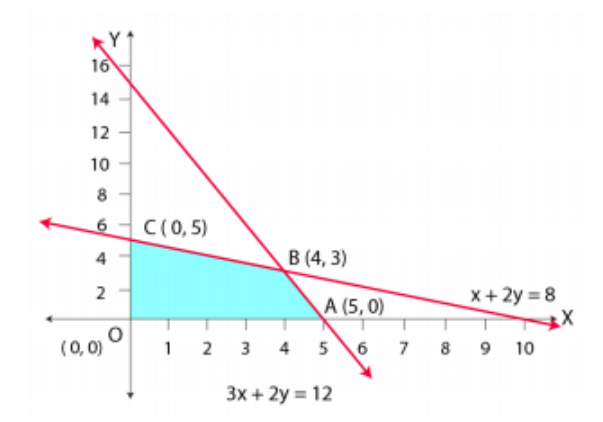
A (6, 0) and B (0, 3) are the corner points of the feasible region.
The values of Z at the corner points are given below.
| Corner point | Z = x + 2y |
| A (6, 0) | 6 |
| B (0, 3) | 6 |
Solution:
The feasible region determined by the constraints,
x
+ 2
y
≤ 120,
x
+
y
≥ 60,
x
− 2
y
≥ 0,
x
≥ 0, and
y
≥ 0, is given below.
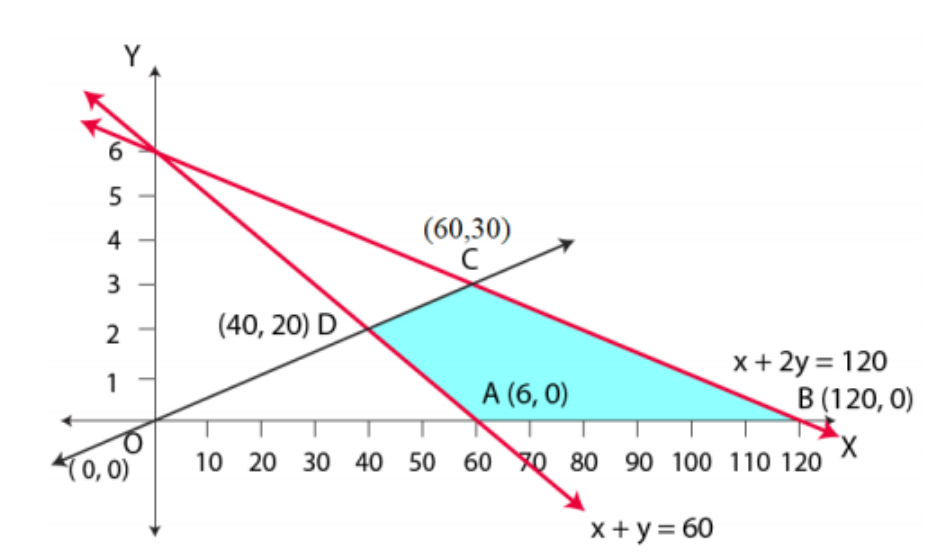A (60, 0), B (120, 0), C (60, 30), and D (40, 20) are the corner points of the feasible region. The values of Z at these corner points are given below.
| Corner point | Z = 5x + 10y | |
| A (60, 0) | 300 | Minimum |
| B (120, 0) | 600 | Maximum |
| C (60, 30) | 600 | Maximum |
| D (40, 20) | 400 |
Solution:
The feasible region determined by the constraints,
x
+ 2
y
≥ 100, 2
x
−
y
≤ 0, 2
x
+
y
≤ 200,
x
≥ 0, and
y
≥ 0, is given below.
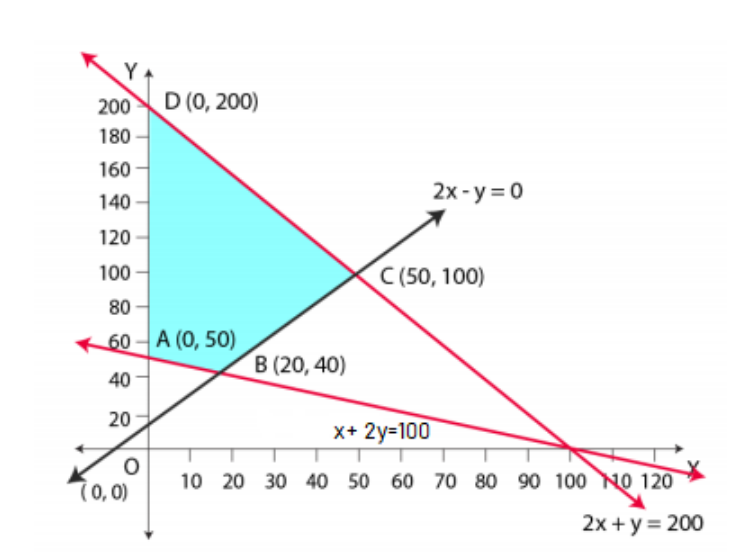A (0, 50), B (20, 40), C (50, 100) and D (0, 200) are the corner points of the feasible region. The values of Z at these corner points are given below.
| Corner point | Z = x + 2y | |
| A (0, 50) | 100 | Minimum |
| B (20, 40) | 100 | Minimum |
| C (50, 100) | 250 | |
| D (0, 200) | 400 | Maximum |
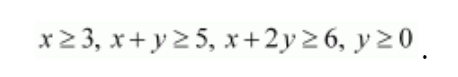Solution:
The feasible region determined by the constraints,
is given below.
Here, it can be seen that the feasible region is unbounded.
The values of Z at corner points A (6, 0), B (4, 1) and C (3, 2) are given below.
| Corner point | Z = – x + 2y |
| A (6, 0) | Z = – 6 |
| B (4, 1) | Z = – 2 |
| C (3, 2) | Z = 1 |
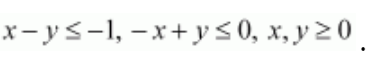Solution:
The region determined by the constraints
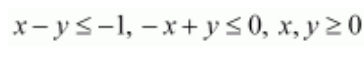
There is no feasible region, and therefore, z has no maximum value.
Exercise 12.2 page no: 519
1. Reshma wishes to mix two types of food, P and Q, in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A, and 11 units of vitamin B. Food P costs Rs 60/kg, and Food Q costs Rs 80/kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture? Solution: Let the mixture contain x kg of food P and y kg of food Q. Hence, x ≥ 0 and y ≥ 0 The given information can be compiled in a table, as given below.| Vitamin A (units/kg) | Vitamin B (units/kg | Cost (Rs/kg) | |
| Food P | 3 | 5 | 60 |
| Food Q | 4 | 2 | 80 |
| Requirement (units/kg) | 8 | 11 |
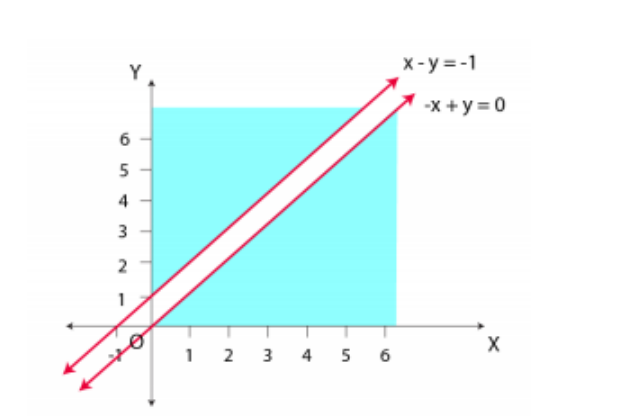
Clearly, we can see that the feasible region is unbounded.
A (8 / 3, 0), B (2, 1 / 2) and C (0, 11 / 2)
The values of Z at these corner points are given below.
| Corner point | Z = 60x + 80 y | |
| A (8 / 3, 0) | 160 | Minimum |
| B (2, 1 / 2) | 160 | Minimum |
| C (0, 11 / 2) | 440 |
| Flour (g) | Fat (g) | |
| Cakes of the first kind, x | 200 | 25 |
| Cakes of the second kind, y | 100 | 50 |
| Availability | 5000 | 1000 |
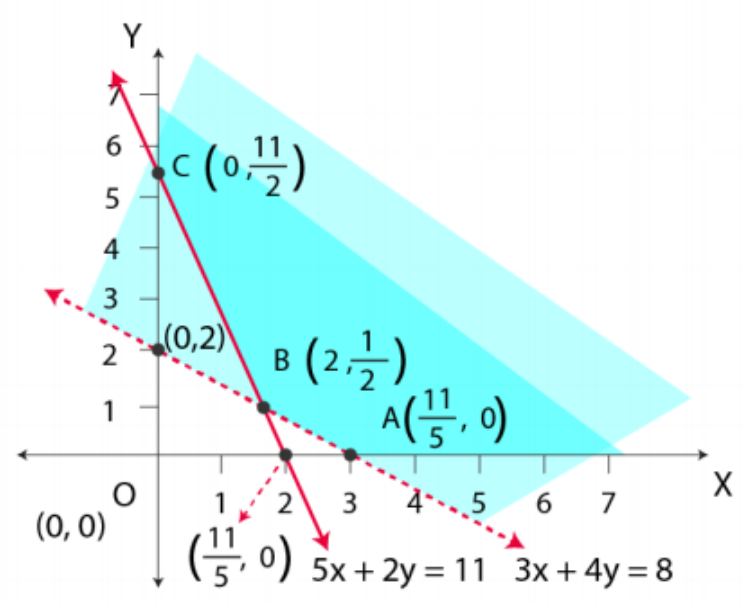
A (25, 0), B (20, 10), O (0, 0) and C (0, 20) are the corner points.
The values of Z at these corner points are as given below.
| Corner point | Z = x + y | |
| A (25, 0) | 25 | |
| B (20, 10) | 30 | Maximum |
| C (0, 20) | 20 | |
| O (0,0) | 0 |
Topics Included in NCERT Solutions for Class 12 Maths Chapter 12
The following Linear Programming topics have been included in this article in accordance with the Linear Programming guidelines mentioned by NCERT.12.1 Introduction
12.2 Linear Programming Problem and its Mathematical Formulation12.2.1 Mathematical formulation of the problem
12.2.2 Graphical method of solving linear programming problems
12.3 Different Types of Linear Programming Problems12.3.1 Manufacturing problems
12.3.2 Diet problems
12.3.3 Transportation problems
NCERT Solutions for Class 12 Maths Chapter 12- Linear Programming
The chapter on Linear Programming is a complete unit carrying five marks of the total marks of eighty. With the miscellaneous exercise, there are two exercises as well. These shall help students form a clear understanding of the concept of Linear Programming. This article on Linear Programming Class 12 discusses the following—- Introduction,
- Related terminology, such as constraints, objective function, optimization,
- Different types of linear programming (L.P.) problems,
- Mathematical formulation of L.P. problems,
- Graphical method of solution for problems in two variables,
- Feasible and infeasible regions (bounded or unbounded),
- Feasible and infeasible solutions, and
- Optimal feasible solutions (up to three non-trivial constraints)
NCERT Solutions for Class 12 Maths Chapter 12- Key Features of Linear Programming
This article on Class 12 Maths Chapter 12 Linear Programming solutions helps students gain a clear understanding of the vital concepts of the subject. It touches upon the key concepts including,- Diet problems
- Manufacturing problems
- Transportation problems
NCERT Solutions for Class 12 Maths Chapter 12 FAQs
What is the concept of Linear Programming?
Linear Programming involves subjecting mathematical functions to constraints which are then maximized or minimized accordingly. This chapter covers objective functions and constraints that are completely linear. The linear functions’ maximum and minimum values are plotted on the xy coordinate for further deductions. Optimising the mathematical functions exposed to linear constraints happens to be the main objective of Linear Programming.
How can I access the NCERT Solutions for Class 12 Maths Chapter 11?
You’ll simply have to visit the Physics Wallah website from where you can download the entire chapter. All the solutions given here have been worked on by experts at Physics Wallah and they are very helpful in understanding Linear Programming.
How does this article help students?
Students can refer to Linear Programming Class 12 solutions included in this article and clear their doubts about the subject. Coupled with regular practice, referring to this article goes a long way in acing Linear Programming.
How much do Class 12 Maths Chapter 12 Linear Programming solutions help students score well in the board exams?
The solutions given here are simple and easy to understand. Well explained solutions to the problems like the ones included here do help score higher marks in the board exams. Of course, regular practice is a must.
How can I form a deep and thorough understanding of Linear Programming?
While referring to this article and regular practice of the solutions help, to go deep into the subject, students shall have to study the textbook thoroughly. Only doing so can help form a strong foundation on Linear Programming.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.