
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1 Applications of Integrals is prepared by academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter-8. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1.NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1 Overview
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1 covers these important topics. Students are encouraged to review each topic thoroughly in order to fully understand the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the outcome of the dedicated effort that the Physics Wallah teachers have been doing to aid students in understanding the ideas covered in this chapter. After going over and rehearsing these responses, the goal is for students to easily score outstanding exam results.NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1: Question 1. Find the area of the region bounded by the curve y 2 = x and the lines x = 1, x = 4 and the x -axis. Solution : The area of the region bounded by the curve,
y
2
=
x
, the lines,
x
= 1 and
x
= 4, and the
x
-axis is the area ABCD.
The area of the region bounded by the curve,
y
2
=
x
, the lines,
x
= 1 and
x
= 4, and the
x
-axis is the area ABCD.

NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
Question 2. Find the area of the region bounded by
y
2
= 9
x
,
x
= 2,
x
= 4 and the
x
-axis in the first quadrant.
Solution :

 Question 3.
Find the area of the region bounded by
x
2
= 4
y
,
y
= 2,
y
= 4 and the
y
-axis in the first quadrant.
Solution :
Question 3.
Find the area of the region bounded by
x
2
= 4
y
,
y
= 2,
y
= 4 and the
y
-axis in the first quadrant.
Solution :
 The area of the region bounded by the curve,
x
2
= 4
y
,
y
= 2, and
y
= 4, and the
y
-axis is the area ABCD.
The area of the region bounded by the curve,
x
2
= 4
y
,
y
= 2, and
y
= 4, and the
y
-axis is the area ABCD.
 Question 4. Find the area of the region bounded by the ellipse
Question 4. Find the area of the region bounded by the ellipse
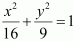 Solution :
The given equation of the ellipse,
Solution :
The given equation of the ellipse,
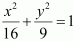 , can be represented as
, can be represented as
 It can be observed that the ellipse is symmetrical about
x
-axis and
y
-axis.
∴ Area bounded by ellipse = 4 × Area of OAB
It can be observed that the ellipse is symmetrical about
x
-axis and
y
-axis.
∴ Area bounded by ellipse = 4 × Area of OAB
 Therefore, area bounded by the ellipse = 4 × 3π = 12π units
Question 5. Find the area of the region bounded by the ellipse
Therefore, area bounded by the ellipse = 4 × 3π = 12π units
Question 5. Find the area of the region bounded by the ellipse
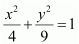 Solution :
The given equation of the ellipse can be represented as
Solution :
The given equation of the ellipse can be represented as
 It can be observed that the ellipse is symmetrical about
x
-axis and
y
-axis.
∴ Area bounded by ellipse = 4 × Area OAB
It can be observed that the ellipse is symmetrical about
x
-axis and
y
-axis.
∴ Area bounded by ellipse = 4 × Area OAB
 Therefore, area bounded by the ellipse = 4 x3π/2 = 6π units.
Question 6.
Find the area of the region in the first quadrant enclosed by
x
-axis, line x = √3y and the circle x
2
+ y
2
= 4
Solution :
The area of the region bounded by the circle, x
2
+ y
2
= 4,x = √3y and the
x
-axis is the area OAB.
Therefore, area bounded by the ellipse = 4 x3π/2 = 6π units.
Question 6.
Find the area of the region in the first quadrant enclosed by
x
-axis, line x = √3y and the circle x
2
+ y
2
= 4
Solution :
The area of the region bounded by the circle, x
2
+ y
2
= 4,x = √3y and the
x
-axis is the area OAB.
 The point of intersection of the line and the circle in the first quadrant is (√3,1).
Area OAB = Area ΔOCA + Area ACB
The point of intersection of the line and the circle in the first quadrant is (√3,1).
Area OAB = Area ΔOCA + Area ACB
 Question 7. Find the area of the smaller part of the circle
x
2
+
y
2
=
a
2
cut off by the line x = a/√2
Solution :
The area of the smaller part of the circle,
x
2
+
y
2
=
a
2
, cut off by the line, x = a/√2, is the area ABCDA.
Question 7. Find the area of the smaller part of the circle
x
2
+
y
2
=
a
2
cut off by the line x = a/√2
Solution :
The area of the smaller part of the circle,
x
2
+
y
2
=
a
2
, cut off by the line, x = a/√2, is the area ABCDA.
 It can be observed that the area ABCD is symmetrical about
x
-axis.
∴ Area ABCD = 2 × Area ABC
It can be observed that the area ABCD is symmetrical about
x
-axis.
∴ Area ABCD = 2 × Area ABC
 Therefore, the area of smaller part of the circle,
x
2
+
y
2
=
a
2
, cut off by the line,
Therefore, the area of smaller part of the circle,
x
2
+
y
2
=
a
2
, cut off by the line,
 Question
8. The area between
x
=
y
2
and
x
= 4 is divided into two equal parts by the line
x
=
a
, find the value of
a
.
Solution :
The line,
x
=
a
, divides the area bounded by the parabola and
x
= 4 into two equal parts.
∴ Area OAD = Area ABCD
Question
8. The area between
x
=
y
2
and
x
= 4 is divided into two equal parts by the line
x
=
a
, find the value of
a
.
Solution :
The line,
x
=
a
, divides the area bounded by the parabola and
x
= 4 into two equal parts.
∴ Area OAD = Area ABCD
 It can be observed that the given area is symmetrical about
x
-axis.
⇒ Area OED = Area EFCD
It can be observed that the given area is symmetrical about
x
-axis.
⇒ Area OED = Area EFCD
 Question
9. Find the area of the region bounded by the parabola
y
=
x
2
and y = |x|
Solution :
The area bounded by the parabola,
x
2
=
y
,and the line,y = |x|, can be represented as
Question
9. Find the area of the region bounded by the parabola
y
=
x
2
and y = |x|
Solution :
The area bounded by the parabola,
x
2
=
y
,and the line,y = |x|, can be represented as
 The given area is symmetrical about
y
-axis.
∴ Area OACO = Area ODBO
The point of intersection of parabola,
x
2
=
y
, and line,
y
=
x
, is A (1, 1).
Area of OACO = Area ΔOAM – Area OMACO
The given area is symmetrical about
y
-axis.
∴ Area OACO = Area ODBO
The point of intersection of parabola,
x
2
=
y
, and line,
y
=
x
, is A (1, 1).
Area of OACO = Area ΔOAM – Area OMACO
 Therefore, required area = 2[1/6] = 1/3 units
Question
10. Find the area bounded by the curve
x
2
= 4
y
and the line
x
= 4
y
– 2
Solution :
The area bounded by the curve,
x
2
= 4
y
, and line,
x
= 4
y
– 2, is represented by the shaded area OBAO.
Therefore, required area = 2[1/6] = 1/3 units
Question
10. Find the area bounded by the curve
x
2
= 4
y
and the line
x
= 4
y
– 2
Solution :
The area bounded by the curve,
x
2
= 4
y
, and line,
x
= 4
y
– 2, is represented by the shaded area OBAO.
 Let A and B be the points of intersection of the line and parabola.
Coordinates of point A are (-1, 1/4).
Coordinates of point B are (2, 1).
We draw AL and BM perpendicular to
x
-axis.
It can be observed that,
Area OBAO = Area OBCO + Area OACO … (1)
Then, Area OBCO = Area OMBC – Area OMBO
Let A and B be the points of intersection of the line and parabola.
Coordinates of point A are (-1, 1/4).
Coordinates of point B are (2, 1).
We draw AL and BM perpendicular to
x
-axis.
It can be observed that,
Area OBAO = Area OBCO + Area OACO … (1)
Then, Area OBCO = Area OMBC – Area OMBO
 Similarly, Area OACO = Area OLAC – Area OLAO
Similarly, Area OACO = Area OLAC – Area OLAO
 Therefore, required area =
Therefore, required area =
 units
Question
11.
Find the area of the region bounded by the curve
y
2
= 4
x
and the line
x
= 3
Solution :
The region bounded by the parabola,
y
2
= 4
x
, and the line,
x
= 3, is the area OACO.
units
Question
11.
Find the area of the region bounded by the curve
y
2
= 4
x
and the line
x
= 3
Solution :
The region bounded by the parabola,
y
2
= 4
x
, and the line,
x
= 3, is the area OACO.
 The area OACO is symmetrical about
x
-axis.
∴ Area of OACO = 2 (Area of OAB)
The area OACO is symmetrical about
x
-axis.
∴ Area of OACO = 2 (Area of OAB)
 Therefore, the required area is 8√3 units.
Question
12. Choose the correct answer:
Therefore, the required area is 8√3 units.
Question
12. Choose the correct answer:
Area lying in the first quadrant and bounded by the circle x 2 + y 2 = 4 and the lines x = 0 and x = 2 is
A. π
B. π/2
C. π/3
D. π/4
Solution : The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as Therefore, option (A) is correct.
Question
13. Choose the correct answer:
Therefore, option (A) is correct.
Question
13. Choose the correct answer:
Area of the region bounded by the curve y 2 = 4 x , y -axis and the line y = 3 is
A. 2
B. 9/4
C. 9/3
D. 9/2
Solution : The area bounded by the curve, y 2 = 4 x , y -axis, and y = 3 is represented as Therefore, option (B) is correct.
Therefore, option (B) is correct.
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1 FAQs
How many exercise are there in application of integrals?
What is the application of integrals?
What is the area under the curve class 12 maths?
What are the two types of integrals?
Why do we use integrals in work?










