
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 (Applications of Integrals)
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 Applications of Integrals is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercises of Chapter 8. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2.NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 Overview
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 covers these important topics. Students are encouraged to review each topic thoroughly in order to fully understand the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the outcome of the dedicated effort that the Physics Wallah teachers have been doing to aid students in understanding the ideas covered in this chapter. After going over and rehearsing these responses, the goal is for students to easily score outstanding exam results.NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2:
Question 1. Find the area of the circle 4 x 2 + 4 y 2 = 9 which is interior to the parabola x 2 = 4 y Solution : The required area is represented by the shaded area OBCDO. Solving the given equation of circle, 4
x
2
+ 4
y
2
= 9, and parabola,
x
2
= 4
y
, we obtain the point of intersection as B(√2,1/2) and D (-√2,1/2).
It can be observed that the required area is symmetrical about
y
-axis.
∴ Area OBCDO = 2 × Area OBCO
We draw BM perpendicular to OA.
Therefore, the coordinates of M are (√2,0).
Therefore, Area OBCO = Area OMBCO – Area OMBO
Solving the given equation of circle, 4
x
2
+ 4
y
2
= 9, and parabola,
x
2
= 4
y
, we obtain the point of intersection as B(√2,1/2) and D (-√2,1/2).
It can be observed that the required area is symmetrical about
y
-axis.
∴ Area OBCDO = 2 × Area OBCO
We draw BM perpendicular to OA.
Therefore, the coordinates of M are (√2,0).
Therefore, Area OBCO = Area OMBCO – Area OMBO
 Therefore, the required area OBCDO is
Therefore, the required area OBCDO is

NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1
Question 2. Find the area bounded by curves ( x – 1) 2 + y 2 = 1 and x 2 + y 2 = 1 Solution : The area bounded by the curves, ( x – 1) 2 + y 2 = 1 and x 2 + y 2 = 1, is represented by the shaded area as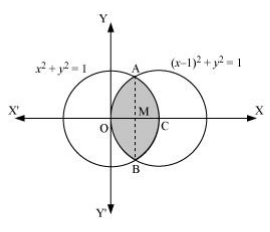 On solving the equations, (
x
– 1)
2
+
y
2
= 1 and
x
2
+
y
2
= 1, we obtain the point of intersection as A (1/2,√3/2) and B (1/2,√3/2) .
It can be observed that the required area is symmetrical about
x
-axis.
∴ Area OBCAO = 2 × Area OCAO
We join AB, which intersects OC at M, such that AM is perpendicular to OC.
The coordinates of M are (1/2,0).
On solving the equations, (
x
– 1)
2
+
y
2
= 1 and
x
2
+
y
2
= 1, we obtain the point of intersection as A (1/2,√3/2) and B (1/2,√3/2) .
It can be observed that the required area is symmetrical about
x
-axis.
∴ Area OBCAO = 2 × Area OCAO
We join AB, which intersects OC at M, such that AM is perpendicular to OC.
The coordinates of M are (1/2,0).
 Therefore, required area OBCAO =
Therefore, required area OBCAO =
 units.
Question 3. Find the area of the region bounded by the curves
y
=
x
2
+ 2,
y
=
x
,
x
= 0 and
x
= 3
Solution :
The area bounded by the curves,
y
=
x
2
+ 2,
y
=
x
,
x
= 0, and
x
= 3, is represented by the shaded area OCBAO as
units.
Question 3. Find the area of the region bounded by the curves
y
=
x
2
+ 2,
y
=
x
,
x
= 0 and
x
= 3
Solution :
The area bounded by the curves,
y
=
x
2
+ 2,
y
=
x
,
x
= 0, and
x
= 3, is represented by the shaded area OCBAO as
 Then, Area OCBAO = Area ODBAO – Area ODCO
Then, Area OCBAO = Area ODBAO – Area ODCO
 Question 4. Using integration, find the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
Solution :
BL and CM are drawn perpendicular to
x
-axis.
It can be observed in the following figure that,
Area (ΔACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)
Question 4. Using integration, find the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
Solution :
BL and CM are drawn perpendicular to
x
-axis.
It can be observed in the following figure that,
Area (ΔACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)

 Therefore, from equation (1), we obtain
Area (ΔABC) = (3 + 5 – 4) = 4 units.
5. Using integration, find the area of the triangular region whose sides have the equations
y
= 2
x
+1,
y
= 3
x
+ 1 and
x
= 4.
Solution :
The equations of sides of the triangle are
y
= 2
x
+1,
y
= 3
x
+ 1, and
x
= 4.
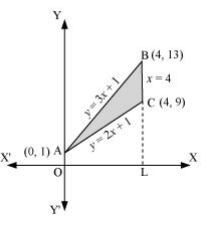
On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13), and C (4, 9).
Therefore, from equation (1), we obtain
Area (ΔABC) = (3 + 5 – 4) = 4 units.
5. Using integration, find the area of the triangular region whose sides have the equations
y
= 2
x
+1,
y
= 3
x
+ 1 and
x
= 4.
Solution :
The equations of sides of the triangle are
y
= 2
x
+1,
y
= 3
x
+ 1, and
x
= 4.
On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13), and C (4, 9).
 It can be observed that,
Area (ΔACB) = Area (OLBAO) –Area (OLCAO)
It can be observed that,
Area (ΔACB) = Area (OLBAO) –Area (OLCAO)
 Question 6. Choose the correct answer:
Smaller area enclosed by the circle
x
2
+
y
2
= 4 and the line
x
+
y
= 2 is
Question 6. Choose the correct answer:
Smaller area enclosed by the circle
x
2
+
y
2
= 4 and the line
x
+
y
= 2 is
(A)2 (π – 2)
(B). π – 2
(C). 2π – 1
(D). 2 (π + 2)
Solution : The smaller area enclosed by the circle, x 2 + y 2 = 4, and the line, x + y = 2, is represented by the shaded area ACBA as It can be observed that,
Area ACBA = Area OACBO – Area (ΔOAB)
It can be observed that,
Area ACBA = Area OACBO – Area (ΔOAB)
 Therefore, option (B) is correct.
Question 7. Choose the correct answer:
Area lying between the curves
y
2
= 4
x
and
y
= 2
x
is
(A) 2/3
(B) 1/3
(C) 1/4
(D) 3/4
Solution :
The area lying between the curve,
y
2
= 4
x
and
y
= 2
x
, is represented by the shaded area OBAO as
Therefore, option (B) is correct.
Question 7. Choose the correct answer:
Area lying between the curves
y
2
= 4
x
and
y
= 2
x
is
(A) 2/3
(B) 1/3
(C) 1/4
(D) 3/4
Solution :
The area lying between the curve,
y
2
= 4
x
and
y
= 2
x
, is represented by the shaded area OBAO as
 The points of intersection of these curves are O (0, 0) and A (1, 2).
We draw AC perpendicular to
x
-axis such that the coordinates of C are (1, 0).
∴ Area OBAO = Area (OCABO) – Area (ΔOCA)
The points of intersection of these curves are O (0, 0) and A (1, 2).
We draw AC perpendicular to
x
-axis such that the coordinates of C are (1, 0).
∴ Area OBAO = Area (OCABO) – Area (ΔOCA)
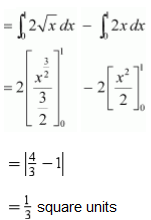 Therefore, option (B) is correct.
Therefore, option (B) is correct.
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 FAQs
Where can I find NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2?
NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 are available on Physics Wallah.
Why are NCERT Solutions important for Class 12 Maths Chapter 8 Exercise 8.2?
NCERT Solutions provide step-by-step explanations and solutions to the questions given in the textbook. They help students understand the concepts better, clarify doubts, and practice solving problems effectively. NCERT Solutions are aligned with the CBSE curriculum, making them essential for exam preparation.
How should I use NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 effectively?
To use NCERT Solutions effectively, students should first attempt to solve the questions on their own. After attempting the questions, they can refer to the NCERT Solutions to verify their answers, understand the solution approach, and learn alternate methods of solving problems. Regular practice with NCERT Solutions enhances problem-solving skills and boosts confidence.
Are NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 helpful for competitive exams?
Yes, NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2 are helpful for various competitive exams, especially those that have a syllabus aligned with the CBSE curriculum.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.









