
NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise (Applications of Integrals)
NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise Applications of Integrals is prepared by academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter-8. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise.NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1
NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise Overview
NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Excercise addresses these significant subjects. In order to fully comprehend the concepts presented in the chapter and make effective use of the provided solutions, it is recommended that students go over each topic in great detail. The intention is for students to effortlessly achieve excellent exam scores after reviewing and practicing these responses.NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise Question 1. Find the area under the given curves and given lines:(i) y = x 2 , x = 1, x = 2 and x -axis
(ii) y = x 4 , x = 1, x = 5 and x –axis
Solution : (i)The required area is represented by the shaded area ADCBA as (ii)The required area is represented by the shaded area ADCBA as
(ii)The required area is represented by the shaded area ADCBA as

NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.2
Question 2. Find the area between the curves y = x and y = x 2 Solution : The required area is represented by the shaded area OBAO as The points of intersection of the curves,
y
=
x
and
y
=
x
2
, is A (1, 1).
We draw AC perpendicular to
x
-axis.
∴ Area (OBAO) = Area (ΔOCA) – Area (OCABO) … (1)
The points of intersection of the curves,
y
=
x
and
y
=
x
2
, is A (1, 1).
We draw AC perpendicular to
x
-axis.
∴ Area (OBAO) = Area (ΔOCA) – Area (OCABO) … (1)
 Question 3. Find the area of the region lying in the first quadrant and bounded by
y
= 4
x
2
,
x
= 0,
y
= 1 and
y
= 4
Solution :
The area in the first quadrant bounded by
y
= 4
x
2
,
x
= 0,
y
= 1, and
y
= 4 is represented by the shaded area ABCDA as
Question 3. Find the area of the region lying in the first quadrant and bounded by
y
= 4
x
2
,
x
= 0,
y
= 1 and
y
= 4
Solution :
The area in the first quadrant bounded by
y
= 4
x
2
,
x
= 0,
y
= 1, and
y
= 4 is represented by the shaded area ABCDA as
 Question 4. Sketch the graph of y = |x + 3| and evaluate
Question 4. Sketch the graph of y = |x + 3| and evaluate
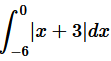 Solution :
The given equation is y = |x + 3|
The corresponding values of
x
and
y
are given in the following table.
Solution :
The given equation is y = |x + 3|
The corresponding values of
x
and
y
are given in the following table.
 On plotting these points, we obtain the graph of y = |x + 3| as follows.
On plotting these points, we obtain the graph of y = |x + 3| as follows.
 Question 5. Find the area bounded by the curve
y
= sin
x
between
x
= 0 and
x
= 2π
Solution :
The graph of
y
= sin
x
can be drawn as
Question 5. Find the area bounded by the curve
y
= sin
x
between
x
= 0 and
x
= 2π
Solution :
The graph of
y
= sin
x
can be drawn as
 ∴ Required area = Area OABO + Area BCDB
∴ Required area = Area OABO + Area BCDB
 Question 6. Find the area enclosed between the parabola
y
2
= 4
ax
and the line
y
=
mx
Solution :
The area enclosed between the parabola,
y
2
= 4
ax
, and the line,
y
=
mx
, is represented by the shaded area OABO as
Question 6. Find the area enclosed between the parabola
y
2
= 4
ax
and the line
y
=
mx
Solution :
The area enclosed between the parabola,
y
2
= 4
ax
, and the line,
y
=
mx
, is represented by the shaded area OABO as
 The points of intersection of both the curves are (0, 0) and
The points of intersection of both the curves are (0, 0) and
 .
We draw AC perpendicular to
x
-axis.
∴ Area OABO = Area OCABO – Area (ΔOCA)
.
We draw AC perpendicular to
x
-axis.
∴ Area OABO = Area OCABO – Area (ΔOCA)
 Question 7. Find the area enclosed by the parabola 4
y
= 3
x
2
and the line 2
y
= 3
x
+ 12
Solution :
The area enclosed between the parabola, 4
y
= 3
x
2
, and the line, 2
y
= 3
x
+ 12, is represented by the shaded area OBAO as
Question 7. Find the area enclosed by the parabola 4
y
= 3
x
2
and the line 2
y
= 3
x
+ 12
Solution :
The area enclosed between the parabola, 4
y
= 3
x
2
, and the line, 2
y
= 3
x
+ 12, is represented by the shaded area OBAO as
 The points of intersection of the given curves are A (–2, 3) and (4, 12).
We draw AC and BD perpendicular to
x-
axis.
∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)
The points of intersection of the given curves are A (–2, 3) and (4, 12).
We draw AC and BD perpendicular to
x-
axis.
∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)
 Question 8. Find the area of the smaller region bounded by the ellipse
Question 8. Find the area of the smaller region bounded by the ellipse
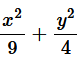 and the line
and the line
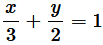 Solution :
The area of the smaller region bounded by the ellipse,
Solution :
The area of the smaller region bounded by the ellipse,
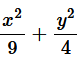 = 1
, and the line,
= 1
, and the line,
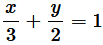 , is represented by the shaded region BCAB as
, is represented by the shaded region BCAB as
 ∴ Area BCAB = Area (OBCAO) – Area (OBAO)
∴ Area BCAB = Area (OBCAO) – Area (OBAO)
 Question 9. Find the area of the smaller region bounded by the ellipse
Question 9. Find the area of the smaller region bounded by the ellipse
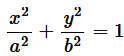 and the line
and the line
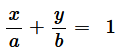 Solution :
The area of the smaller region bounded by the ellipse,
Solution :
The area of the smaller region bounded by the ellipse,
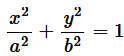 , and the line,
, and the line,
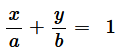 , is represented by the shaded region BCAB as
, is represented by the shaded region BCAB as
 ∴ Area BCAB = Area (OBCAO) – Area (OBAO)
∴ Area BCAB = Area (OBCAO) – Area (OBAO)
 Question 10. Find the area of the region enclosed by the parabola
x
2
=
y
, the line
y
=
x
+ 2 and
x
-axis
Solution :
The area of the region enclosed by the parabola,
x
2
=
y
, the line,
y
=
x
+ 2, and
x
-axis is represented by the shaded region OACO as
Question 10. Find the area of the region enclosed by the parabola
x
2
=
y
, the line
y
=
x
+ 2 and
x
-axis
Solution :
The area of the region enclosed by the parabola,
x
2
=
y
, the line,
y
=
x
+ 2, and
x
-axis is represented by the shaded region OACO as
 The point of intersection of the parabola,
x
2
=
y
, and the line,
y
=
x
+ 2, is A (–1, 1) and C(2, 4).
The point of intersection of the parabola,
x
2
=
y
, and the line,
y
=
x
+ 2, is A (–1, 1) and C(2, 4).
 Question 11.Using the method of integration, find the area enclosed by the curve |x| + |y| = 1
Question 11.Using the method of integration, find the area enclosed by the curve |x| + |y| = 1
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
Solution : The area bounded by the curve, |x| + |y| = 1, is represented by the shaded region ADCB as The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0).
It can be observed that the given curve is symmetrical about
x
-axis and
y
-axis.
∴ Area ADCB = 4 × Area OBAO
The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0).
It can be observed that the given curve is symmetrical about
x
-axis and
y
-axis.
∴ Area ADCB = 4 × Area OBAO
 Question 12. Find the area bounded by curves {(x, y) : y ≥ x
2
and y = |x|}.
Solution :
The area bounded by the curves, {(x, y) : y ≥ x
2
and y = |x|}
.
, is represented by the shaded region as
Question 12. Find the area bounded by curves {(x, y) : y ≥ x
2
and y = |x|}.
Solution :
The area bounded by the curves, {(x, y) : y ≥ x
2
and y = |x|}
.
, is represented by the shaded region as
 It can be observed that the required area is symmetrical about
y
-axis.
It can be observed that the required area is symmetrical about
y
-axis.
 Question 13.Using the method of integration, find the area of the triangle whose vertices are A (2, 0), B (4, 5) and C (6, 3).
Solution :
Vertices of the given triangle are A (2, 0), B (4, 5) and C (6, 3).
Question 13.Using the method of integration, find the area of the triangle whose vertices are A (2, 0), B (4, 5) and C (6, 3).
Solution :
Vertices of the given triangle are A (2, 0), B (4, 5) and C (6, 3).
 Equation of side AB is
Equation of side AB is
 Equation of side BC
Equation of side BC
 Equation of side CA is
Equation of side CA is
 Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)
Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)
 Question 14.Using the method of integration, find the area of the region bounded by the lines: 2
x
+
y
= 4, 3
x
– 2
y
= 6 and
x
– 3
y
+ 5 = 0
Solution :
The given equations of lines are
2
x
+
y
= 4 … (1)
3
x
– 2
y
= 6 … (2)
And,
x
– 3
y
+ 5 = 0 … (3)
Question 14.Using the method of integration, find the area of the region bounded by the lines: 2
x
+
y
= 4, 3
x
– 2
y
= 6 and
x
– 3
y
+ 5 = 0
Solution :
The given equations of lines are
2
x
+
y
= 4 … (1)
3
x
– 2
y
= 6 … (2)
And,
x
– 3
y
+ 5 = 0 … (3)
 The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on
x
-axis.
Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)
The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on
x
-axis.
Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)
 Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}.
Solution :
The area bounded by the curves, {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}, is represented as
Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}.
Solution :
The area bounded by the curves, {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}, is represented as
 The points of intersection of both the curves are (1/2,√2) and (1/2, -√2).
The required area is given by OABCO.
It can be observed that area OABCO is symmetrical about
x
-axis.
∴ Area OABCO = 2 × Area OBC
Area OBCO = Area OMC + Area MBC
The points of intersection of both the curves are (1/2,√2) and (1/2, -√2).
The required area is given by OABCO.
It can be observed that area OABCO is symmetrical about
x
-axis.
∴ Area OABCO = 2 × Area OBC
Area OBCO = Area OMC + Area MBC
 Therefore, the required area is
Therefore, the required area is
 units.
Question 16.Choose the correct answer:
units.
Question 16.Choose the correct answer:
Area bounded by the curve y = x 3 , the x -axis and the ordinates x = –2 and x = 1 is
(A) -9 (B) -15/4 (C) 15/4 (D) 17/4 Solution : Therefore, option (D) is correct.
Question 17.Choose the correct answer:
The area bounded by the curve y = x|x|, axis and the ordinates
x
= –1 and
x
= 1 is given by:
Therefore, option (D) is correct.
Question 17.Choose the correct answer:
The area bounded by the curve y = x|x|, axis and the ordinates
x
= –1 and
x
= 1 is given by:
[Hint: y = x 2 if x > 0 and y = – x 2 if x < 0]
(A) 0 (B) 1/3 (C) 2/3 (D) 4/3 Solution : Therefore, option (C) is correct.
Question 18.Choose the correct answer:
Therefore, option (C) is correct.
Question 18.Choose the correct answer:
The area of the circle x 2 + y 2 = 16 exterior to the parabola y 2 = 6 x is
 Solution :
The given equations are
x
2
+
y
2
= 16 … (1)
y
2
= 6
x
… (2)
Solution :
The given equations are
x
2
+
y
2
= 16 … (1)
y
2
= 6
x
… (2)
 Area bounded by the circle and parabola
Area bounded by the circle and parabola
 Thus, the correct answer is C.
Question 19.Choose the correct answer:
Thus, the correct answer is C.
Question 19.Choose the correct answer:
The area bounded by the y -axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2.
(A) 2(√2 - 1) (B) √2 - 1 (C) √2 + 1 (D) √2 Solution : The given equations are y = cos x … (1) And, y = sin x … (2) Required area = Area (ABLA) + area (OBLO)
Required area = Area (ABLA) + area (OBLO)
 Required area = Area (AB
Therefore, option (B) is correct.
Required area = Area (AB
Therefore, option (B) is correct.
NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise FAQs
What is the Miscellaneous Exercise in Class 12 Maths Chapter 8 about?
Why is it important to practice the Miscellaneous Exercise in Class 12 Maths Chapter 8?
How can NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise aid in exam preparation?
Can NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise be used for self-study?










