Physics Wallah

NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1

Access NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1, covering the basics of trigonometry. Get step by step solutions to help you understand trigonometric ratios and their applications.
NCERT Solutions
Notes
PYQ
Important Questions
Sample Paper

Chapter 8 Introduction to Trigonometry Exercise 8.1 Class 10 Solutions: NCERT Solutions of Chapter 8 Exercise 8.1 introduces students to fundamental trigonometric ratios—sine, cosine, tangent, secant, cosecant, and cotangent—based on a right-angled triangle. This exercise 8.1 solutions explain each ratio step-by-step, making it simple for learners to understand how sides of a triangle relate to each ratio.

Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1 Solutions

Below are the detailed NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1. These step-by-step explanations will help students understand the basics of trigonometric ratios and apply them accurately while solving problems
 
1. In Δ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C

Answer:

Let us draw a right-angled triangle ABC, right-angled at B. Using Pythagoras' theorem
, chapter 8-Introduction to Trigonometry Exercise 8.1/image004.png
(i) chapter 8-Introduction to Trigonometry Exercise 8.1/image005.png
 chapter 8-Introduction to Trigonometry Exercise 8.1/image008.png


(ii) chapter 8-Introduction to Trigonometry Exercise 8.1/image009.png chapter 8-Introduction to Trigonometry Exercise 8.1/image010.png ,
 2. In the adjoining figure, find tan P – cot R.
  chapter 8-Introduction to Trigonometry Exercise 8.1/image013.png

Answer:

chapter 8-Introduction to Trigonometry Exercise 8.1/image015.png
chapter 8-Introduction to Trigonometry Exercise 8.1/image007.png

 
3. If sin A =3/4, calculate cos A and tan A. 

Answer:

Given: A triangle ABC in which
 chapter 8-Introduction to Trigonometry Exercise 8.1/image024.png
B =90. We know that sin A = BC/AC = 3/4.
Let BC be 3k, and AC will be 4k, where k is a positive real number.
By Pythagoras theorem we get, AC  2 = AB 2 + BC 2 (4k) 2 = AB 2 + (3k) 2 16k 2 - 9k 2 = AB 2 AB 2 = 7k 2 AB = √7 k cos A = AB/AC = √7 k/4k = √7/4 tan A = BC/AB = 3k/√7 k = 3/√7

 
4. Given 15 cot A = 8, find sin A and sec A. 

Answer:

NCERT solutions for class 10 maths/image040.jpg

Let ΔABC be a right-angled triangle, right-angled at B. 
We know that cot A = AB/BC = 8/15  

(Given). Let AB be 8k, and BC will be 15k, where k is a positive real number.
By Pythagoras theorem we get, AC  2 = AB 2 + BC 2 AC 2 = (8k) 2 + (15k) 2 AC 2 = 64k 2 + 225k 2 AC 2 = 289k 2 AC = 17 k sin A = BC/AC = 15k/17k = 15/17 sec A = AC/AB = 17k/8 k = 17/8
 
5. Given sec θ = 13/12, calculate all other trigonometric ratios.

Answer:

Consider a triangle ABC in which
 NCERT solutions for class 10 maths/image024.png

We know that the sec function is the reciprocal of the cos function, which is equal to the ratio of the length of the hypotenuse side to the adjacent side

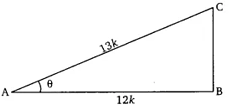
Let us assume a right-angled triangle ABC, right-angled at B

sec θ =13/12 = Hypotenuse/Adjacent side = AC/AB

Let AC be 13k and AB will be 12k

Where k is a positive real number.

According to the Pythagoras theorem, the square of the hypotenuse side is equal to the sum of the squares of the other two sides of a right-angle triangle, and we get,

AC2=AB2 + BC2

Substitute the value of AB and AC

(13k)2= (12k)2 + BC2

169k2= 144k2 + BC2

169k2= 144k2 + BC2

BC2 = 169k2 – 144k2

BC2= 25k2

Therefore, BC = 5k

Now, substitute the corresponding values in all other trigonometric ratios

So,

Sin θ = Opposite Side/Hypotenuse = BC/AC = 5/13

Cos θ = Adjacent Side/Hypotenuse = AB/AC = 12/13

tan θ = Opposite Side/Adjacent Side = BC/AB = 5/12

Cosec θ = Hypotenuse/Opposite Side = AC/BC = 13/5

cot θ = Adjacent Side/Opposite Side = AB/BC = 12/5

 
6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
  NCERT solutions for class 10 maths/image065.jpg

Answer:

cos  A = cos But NCERT solutions for class 10 maths/image068.png
 
7. If cot θ =7/8, evaluate :  (i)(1+sin θ )(1-sin θ)/(1+cos θ)(1-cos θ) (ii) cot 2 θ

Answer:

Consider a triangle ABC
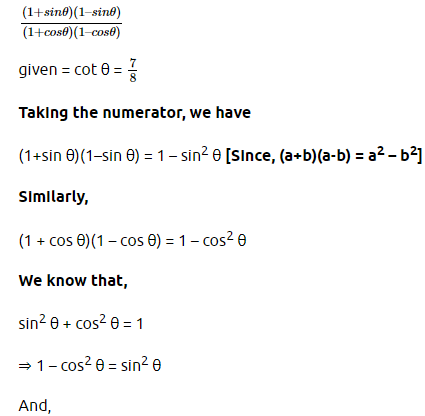 NCERT solutions for class 10 maths/image051.png NCERT solutions for class 10 maths/image073.png (ii) NCERT solutions for class 10 maths/image074.png NCERT solutions for class 10 maths/image041.png

 8. If 3cot A = 4/3 , check whether (1-tan 2 A)/(1+tan 2 A) = cos 2 A – sin 2 A or not.

Answer:



Consider a triangle ABC AB=4cm, BC= 3cm NCERT solutions for class 10 maths/image024.png . NCERT solutions for class 10 maths/image090.png And NCERT solutions for class 10 maths/image091.png NCERT solutions for class 10 maths/image007.png NCERT solutions for class 10 maths/image092.png
 
9. In triangle ABC, right-angled at B, if tan A =1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C

Answer:

Consider a triangle ABC in which NCERT solutions for class 10 maths/image024.png .
(i) NCERT solutions for class 10 maths/image112.png
(ii) NCERT solutions for class 10 maths/image113.png
10. In Δ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Answer:

Given that, PR + QR = 25 , PQ = 5. Let PR be x.  ∴ QR = 25 - x By Pythagoras theorem , PR2 = PQ 2 + QR 2 x 2 = (5)2 + (25 - x) 2 x 2 = 25 + 625 + x 2 - 50x 50x = 650 x = 13 ∴ PR = 13 cm QR = (25 - 13) cm = 12 cm sin P = QR/PR = 12/13 cos P = PQ/PR = 5/13 tan P = QR/PQ = 12/5

11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A. "
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A. (v) sin θ = 4/3 for some angle θ.

Answer:

i) False. In ΔABC in which ∠B = 90º, AB = 3, BC = 4 and AC = 5 Value of tan A = 4/3 which is greater than. The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem. AC 2 = AB 2 + BC 2 5 2 = 3 2 + 4 2 25 = 9 + 16 25 = 25

(ii) True. Let a ΔABC in which ∠B = 90º,AC be 12k and AB be 5k, where k is a positive real number. By Pythagoras' theorem, we get, AC 2 = AB 2 + BC 2 (12k) 2 = (5k) 2 + BC 2 BC 2 + 25k 2 = 144k 2 BC 2 = 119k 2 Such a triangle is possible as it will follow the Pythagoras theorem.

(iii) False. Abbreviation used for cosecant of angle A is cosec A.cos A is the abbreviation used for cosine of angle A.

(iv) False. cot A is not the product of cot and A. It is the cotangent of ∠A. (v) False. sin θ = Height/Hypotenuse. We know that in a right-angled triangle, the Hypotenuse is the longest side. ∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.
 

Exercise 8.1 Introduction to Trigonometry Class 10 PDF

These NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1 help students understand the basics of trigonometric ratios through clear, step-by-step explanations. Aligned with the latest CBSE syllabus, these solutions make it easier to grasp concepts, practice accurately, and prepare confidently for exams. Click below to download the PDF for quick revision and effective learning. These are ideal for students looking for an introduction to trigonometry class 10 NCERT solutions.

 
Exercise 8.1 Introduction to Trigonometry Class 10 PDF


Introduction to Trigonometry Class 10 Maths Chapter 8 Exercise 8.1 FAQs

What is trigonometry?

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles.

Why is trigonometry important?

Trigonometry is crucial for solving problems in various fields, including physics, engineering, architecture, astronomy, and navigation. It helps in calculating heights, distances, and angles accurately.

What does Exercise 8.1 in Chapter 8 cover?

Exercise 8.1 introduces the definitions of basic trigonometric ratios with respect to a right-angled triangle and helps students understand their properties and relationships.

Are trigonometric ratios applicable to all triangles?

Trigonometric ratios are specifically defined for right-angled triangles, but their principles can be extended using laws like the sine law and cosine law for any triangle.
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App