CBSE Class 10 Maths Notes Chapter 8 Introduction to Trigonometry
Here, we have provided CBSE Class 10 Maths Notes Chapter 8. Students can view these CBSE Class 10 Maths Notes Chapter 8 Introduction to Trigonometry before exams for better understanding of the chapter.
Neha Tanna19 Apr, 2024
Share
CBSE Class 10 Maths Notes Chapter 8: Here are the notes for Class 10 Math's trigonometry unit. One of the areas of mathematics where we study the relationships between a triangle's angles and sides is trigonometry. The Greek terms "tri" (meaning three), "gon" (meaning sides), and "metron" (meaning measure) are the root of the word trigonometry. We shall study the fundamentals of trigonometry in this chapter.
Learn the entire trigonometry topic that is taught in maths class 10. Get the different trigonometric ratios for different angles as well as the trigonometric function relationships, trigonometry tables, and other identities provided here.CBSE Class 10 Syllabus 2024-25
CBSE Class 10 Maths Notes Chapter 8 PDF
To gain a clear understanding of these concepts, you can refer to our Class 10 Maths Chapter 8 Notes for shortcut methods and detailed instructions. For future use, you can also download our CBSE Class 10 Maths Notes Chapter 8.CBSE Class 10 Maths Notes Chapter 8 PDF
CBSE Class 10 Maths Notes Chapter 8
The hypotenuse is AC, the side next to ∠A is AB, and the side opposite ∠A is BC in the ΔABC right-angled at B.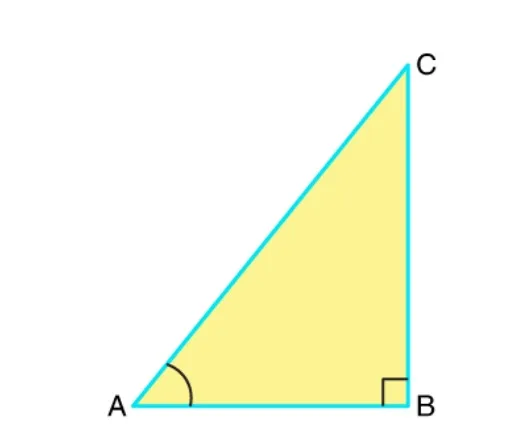
Trigonometric Ratios
For the right Δ A B C , right-angled at ∠ B , the trigonometric ratios of the ∠ A are as follows:- sin A=opposite side/hypotenuse=BC/AC
- cos A=adjacent side/hypotenuse=AB/AC
- tan A=opposite side/adjacent side=BC/AB
- cosec A=hypotenuse/opposite side=AC/BC
- sec A=hypotenuse/adjacent side=AC/AB
- cot A=adjacent side/opposite side=AB/BC
Relation between Trigonometric Ratios
- cosec θ =1/sin θ
- sec θ = 1/cos θ
- tan θ = sin θ/cos θ
- cot θ = cos θ/sin θ=1/tan θ
Visualization of Trigonometric Ratios Using a Unit Circle
Draw a circle with the origin in its centre and a radius of one unit. Examine a line segment OP that forms an angle with the x-axis by connecting a point P on the circle to the centre. To cut it at Q, draw a perpendicular from P to the x-axis.- sin θ=PQ/OP=PQ/1=PQ
- cos θ=OQ/OP=OQ/1=OQ
- tan θ=PQ/OQ=sin θ/cos θ
- cosec θ=OP/PQ=1/PQ
- sec θ=OP/OQ=1/OQ
- cot θ=OQ/PQ=cos θ/sin θ
Trigonometric Ratios of Specific Angles
The specific angles that are defined for trigonometric ratios are 0°, 30°, 45°, 60° and 90°.Trigonometric Ratios of 45°
If one of the angles of a right-angled triangle is 45°, then another angle will also be equal to 45°.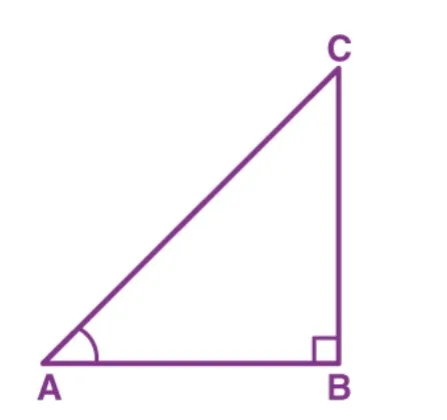
Let us say ABC is a right-angled triangle at B, such that;
∠ A = ∠ C = 45°
Thus, BC = AB = a (say)
Using Pythagoras theorem, we have;
AC
2
= AB
2
+ BC
2
= a
2
+ a
2
= 2a
2
AC = a√2
Now, from the trigonometric ratios, we have;
- sin 45° = (Opp. side to angle 45°)/Hypotenuse = BC/AC = a/a√2 = 1/√2
- cos 45° = (Adj. side to angle 45°)/Hypotenuse = AB/AC = a/a√2 = 1/√2
- tan 45° = BC/AB = a/a = 1
- cosec 45° = 1/sin 45° = √2
- sec 45° = 1/cos 45° = √2
- cot 45° = 1/tan 45° = 1
Trigonometric Ratios of 30° and 60°
Here, we will consider an equilateral triangle ABC, such that; AB = BC = AC = 2a ∠A = ∠B = ∠C = 60° Now, draw a perpendicular AD from vertex A that meets BC at D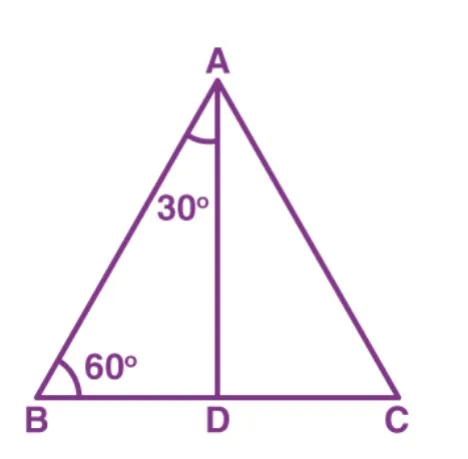
According to the congruency of the triangle, we can say;
Δ ABD ≅ Δ ACD
Hence,
BD = DC
∠ BAD = ∠ CAD (By CPCT)
Now, in triangle ABD, ∠ BAD = 30° and ∠ ABD = 60°
Using Pythagoras theorem,
AD
2
= AB
2
– BD
2
= (2a)
2
– (a)
2
= 3a
2
AD = a√3
So, the trigonometric ratios for a 30-degree angle will be;
sin 30° = BD/AB = a/2a = 1/2
cos 30° = AD/AB = a√3/2a = √3/2
tan 30° = BD/AD = a/a√3 = 1/√3
Also,
cosec 30° = 1/sin 30 = 2
sec 30° = 1/cos 30 = 2/√3
cot 30° = 1/tan 30 = √3
Similarly, we can derive the values of trigonometric ratios for 60°.
- sin 60° = √3/2
- cos 60° = 1/2
- tan 60° = √3
- cosec 60° = 2/√3
- sec 60° = 2
- cot 60° = 1/√3
Trigonometric Ratios of 0° and 90°
In the event that ∠A is decreased and ABC forms a right-angled triangle at B, side AC will approach side AB. Accordingly, when ∠ A approaches zero, AC approaches AB and BC approaches zero. Hence, Sin A = BC /AC = 0 and cos A = AB/AC = 1 tan A = sin A/cos A = 0/1 = 0 Also, cosec A = 1/sin A = 1/0 = not defined sec A = 1/cos A = 1/1 = 1 cot A = 1/tan A = 1/0 = not defined The values of trigonometric ratios for a 90-degree angle can be found in a similar manner. In this case, angle C becomes zero, and side AB will approach side BC to make angle A nearly 90 degrees and side AB almost zero.Range of Trigonometric Ratios from 0 to 90 Degrees
For 0∘≤θ≤90∘,- 0 ≤ sin θ ≤ 1
- 0 ≤ cos θ ≤ 1
- 0 ≤ tan θ < ∞ 1 ≤ sec θ < ∞
- 0 ≤ cot θ < ∞
- 1 ≤ cosec θ < ∞
Standard Values of Trigonometric Ratios
| ∠A | 0 o | 30 o | 45 o | 60 o | 90 o |
| sin A | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| cos A | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| tan A | 0 | 1/√3 | 1 | √3 | not defined |
| cosec A | not defined | 2 | √2 | 2/√3 | 1 |
| sec A | 1 | 2/√3 | √2 | 2 | not defined |
| cot A | not defined | √3 | 1 | 1/√3 | 0 |
Benefits of CBSE Class 10 Maths Notes Chapter 8
Experts in the field have put together our Class 10 PDF Trigonometry Notes to provide you with the best review materials. They are aware of the challenges students have when studying trigonometry because they have instructed thousands of students in more than a thousand cities. For this reason, the Class 10 Maths Chapter 8 Notes include step-by-step compilation and shortcut procedures. It will be easier for you to comprehend the same if you revise from here. This is a synopsis of the main points of the chapter for your knowledge.CBSE Class 10 Maths Notes Chapter 8 FAQs
What is the 8th chapter of maths class 10?
Chapter 8 consists of the discussion of basic trigonometry, opposite & adjacent sides in a right-angled triangle, basic trigonometric ratios, and standard values of trigonometric ratios and complementary trigonometric ratios.
What is the introduction of trigonometry class?
Trigonometry is one of the most important branches in mathematics.
Is class 10 trigonometry hard?
Trigonometry in Class 10 can seem challenging to some students, but with proper understanding and practice, it can become manageable. The difficulty level may vary from student to student based on their familiarity with mathematical concepts and their problem-solving skills.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App