Introduction to Trigonometry Class 10 Exercise 8.2: NCERT Class 10 Maths Chapter 8 Exercise 8.2 is a crucial part of the CBSE syllabus on Introduction to Trigonometry, focusing on trigonometric ratios for standard angles (0°, 30°, 45°, 60°, 90°) through evaluation, true/false, and application problems that frequently appear in board exams.
This exercise is essential for scoring 4-6 marks in short-answer questions, as it reinforces quick recall of sin, cos, tan values and their complementary angle relationships, directly linking to heights/distances in Chapter 9. Regular practice ensures exam readiness. These solutions provide clear explanations and step-by-step methods to help students grasp the concepts effectively and build confidence in solving trigonometric problems.
Class 10 Maths Introduction to Trigonometry Exercise 8.2
Below are the NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry Exercise 8.2, presented in a clear and student-friendly manner.Solve the following Questions.
1. Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60

Solution:
(i) sin 60° cos 30° + sin 30° cos 60°
First, find the values of the given trigonometric ratios
sin 30° = 1/2
cos 30° = √3/2
sin 60° = 3/2
cos 60°= 1/2
Now, substitute the values in the given problem
sin 60° cos 30° + sin 30° cos 60° = √3/2 ×√3/2 + (1/2) ×(1/2 ) = 3/4+1/4 = 4/4 =1
(ii) 2 tan2 45° + cos2 30° – sin2 60
We know that the values of the trigonometric ratios are:
sin 60° = √3/2
cos 30° = √3/2
tan 45° = 1
Substitute the values in the given problem
2 tan2 45° + cos2 30° – sin2 60 = 2(1)2 + (√3/2)2-(√3/2)2
2 tan2 45° + cos2 30° – sin2 60 = 2 + 0
2 tan2 45° + cos2 30° – sin2 60 = 2
(iii) cos 45°/(sec 30°+cosec 30°)
We know that,
cos 45° = 1/√2
sec 30° = 2/√3
cosec 30° = 2
Substituting the values, we get

Now, multiply both the numerator and denominator by √2 , we get

Therefore, cos 45°/(sec 30°+cosec 30°) = (3√2 – √6)/8

We know that,
sin 30° = 1/2
tan 45° = 1
cosec 60° = 2/√3
sec 30° = 2/√3
cos 60° = 1/2
cot 45° = 1
Substituting the values in the given problem, we get


We know that,
cos 60° = 1/2
sec 30° = 2/√3
tan 45° = 1
sin 30° = 1/2
cos 30° = √3/2
Now, substitute the values in the given problem, we get
(5cos260° + 4sec230° – tan245°)/(sin2 30° + cos2 30°)
= 5(1/2)2+4(2/√3)2-12/(1/2)2+(√3/2)2
= (5/4+16/3-1)/(1/4+3/4)
= (15+64-12)/12/(4/4)
= 67/12
2. Choose the correct option and justify your choice :
(i) 2tan 30°/1+tan 2 30° = (A) sin 60° (B) cos 60° (C) tan 60° (D) sin 30°
(iii) sin 2 A = 2 sin A is true when A = (A) 0° (B) 30° (C) 45° (D) 60°
(iv) 2tan30°/1-tan 2 30° = (A) cos 60° (B) sin 60° (C) tan 60° (D) sin 30°
Answer:
(i) 2tan 30°/1+tan 2 30° = (A) sin 60° (B) cos 60° (C) tan 60° (D) sin 30° =

(iii) sin 2 A = 2 sin A is true when A = (A) 0° (B) 30° (C) 45° (D) 60°


3. If tan (A + B) = √3 and tan (A – B) = 1/√3; 0° < A + B ≤ 90°; A > B, find A and B.
Answer:
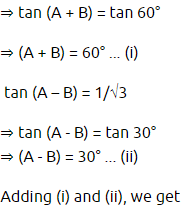


(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Answer:
(i) False. Let A = 30° and B = 60°, then sin (A + B) = sin (30° + 60°) = sin 90° = 1 and, sin A + sin B = sin 30° + sin 60° = 1/2 + √3/2 = 1+√3/2(ii) True. sin 0° = 0 sin 30° = 1/2 sin 45° = 1/√2 sin 60° = √3/2 sin 90° = 1 Thus the value of sin θ increases as θ increases.
(iii) False. cos 0° = 1 cos 30° = √3/2 cos 45° = 1/√2 cos 60° = 1/2 cos 90° = 0 Thus the value of cos θ decreases as θ increases.
(iv) True. cot A = cos A/sin A cot 0° = cos 0°/sin 0° = 1/0 = undefined.
Class 10 Introduction to Trigonometry Exercise 8.2 PDF
The Class 10 Introduction to Trigonometry Exercise 8.2 PDF offers clear, step-by-step solutions designed as per the CBSE Class 10 Maths syllabus. It covers essential trigonometric identities and fundamental ratio transformations, helping students revise quickly and strengthen accuracy. This PDF is ideal for focused practice and effective exam preparation.
Introduction to Trigonometry Class 10 Exercise 8.2 PDF
Explore More Chapters|
|
