
Platonic Solids, also referred to as regular solids or regular polyhedra, are three-dimensional geometric shapes characterized by identical faces, each made up of congruent and convex regular polygons. These polyhedra were originally explored by ancient Greeks, who sometimes referred to them as cosmic solids. There are five distinct types of Platonic solids. It has been suggested that these five Platonic solids, believed to exist in the natural world, symbolize the five classical elements: earth, air, fire, water, and the universe. In this discussion, we will delve into the realm of Platonic solids, exploring their properties, various types, and solving a few illustrative examples.
Definition of Platonic Solids
A Platonic solid is a three-dimensional shape characterized by identical faces, each of which is a regular polygon, and an equal number of faces meeting at each vertex. These regular, convex polyhedra are named Platonic solids. There are five distinct types of Platonic solids, each identified by the number of faces it possesses. These five solids are traditionally associated with the five elements of nature: Earth, Air, Fire, Water, and the Universe. The philosopher Plato, who closely studied Platonic solids, linked each of these shapes to aspects of the natural world. The five types of Platonic solids are as follows:
- Tetrahedron
- Cube
- Octahedron
- Dodecahedron
- Icosahedron
Plato attributed the element of fire to the tetrahedron, associated earth with the cube, connected water with the icosahedron, linked air to the octahedron, and saw the universe represented by the dodecahedron.
Properties of Platonic Solids
Platonic solids possess distinct properties that set them apart from other geometric shapes, and these characteristics include:
All faces are regular and congruent.
Platonic solids are convex polyhedra.
Faces of Platonic solids do not intersect except at their edges.
The same number of faces meet at each vertex.
Platonic solids have polygonal faces that are similar in shape, height, angles, and edges.
They are three-dimensional, convex, and regular solid shapes.
Types of Platonic Solids
Let's delve into the five types of Platonic solids, each with its unique properties and distinct shapes:
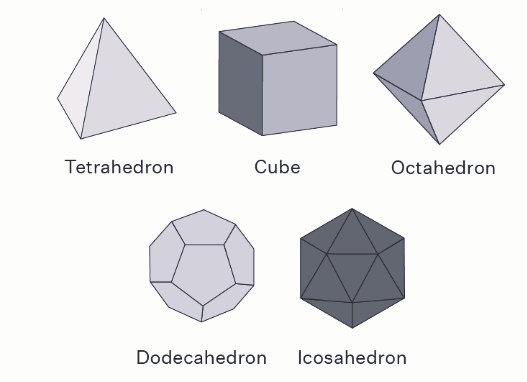
Tetrahedron
The tetrahedron, often referred to as a triangular pyramid in geometry, is one of the Platonic solids. It is characterized by the following properties:
Faces, Edges, and Vertices:
A tetrahedron has 4 triangular faces.
It possesses 6 straight edges.
There are 4 vertices (corners).
Equidistant Vertices:
All four vertices are equidistant from each other. This means that the distances between any pair of vertices are the same.
Symmetry:
A tetrahedron has 6 planes of symmetry, which are planes that divide it into two equal halves.
Parallel Faces:
Unlike some other Platonic solids, a tetrahedron does not have parallel faces. All of its faces are triangular and none run parallel to each other.
Regular Tetrahedron:
In the case of a regular tetrahedron, all of its faces are equilateral triangles, meaning they have equal sides and equal angles.
The tetrahedron is a simple yet intriguing geometric shape with these unique characteristics, making it a fundamental building block in the study of three-dimensional geometry.
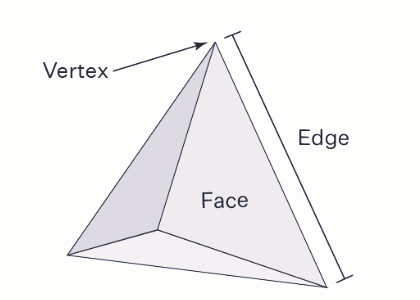
Cube
A cube is a three-dimensional solid object with distinct properties:
Faces, Edges, and Vertices:
A cube consists of 6 square faces.
It possesses 12 edges.
There are 8 vertices (corners).
Equal-Sided Faces:
All the faces of a cube are square-shaped, which means that the length, breadth, and height are the same. In other words, all sides of the cube are of equal length.
Right Angles:
The angles between any two faces or surfaces of a cube are 90 degrees, forming right angles at the edges.
Parallel Faces and Edges:
The opposite faces of a cube are parallel to each other, and the opposite edges are also parallel.
Intersecting Faces:
Each face of the cube meets the other four faces, sharing edges and vertices.
Vertex Connectivity:
Each vertex of the cube is connected to three faces and three edges, contributing to the cube's regular and symmetrical structure.
Cubes are a fundamental geometric shape and are often associated with symmetry, simplicity, and stability. These properties make them important in various fields, including mathematics, engineering, and design.
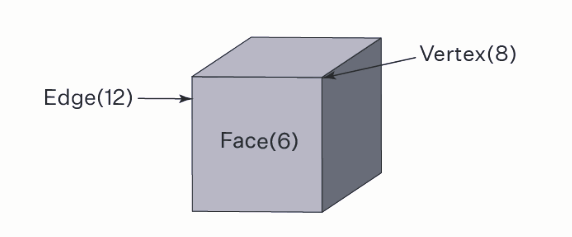
Octahedron
An octahedron is a polyhedron characterized by the following properties:
Faces, Edges, and Vertices:
An octahedron has 8 faces.
It possesses 12 edges.
There are 6 vertices (corners).
Vertex Connectivity:
At each vertex of an octahedron, 4 edges meet, creating a unique vertex arrangement.
Equilateral Triangle Faces:
In the case of a regular octahedron, all 8 faces are shaped like equilateral triangles. This means that all sides of these triangles are of equal length, and all angles within these triangles are equal.
The octahedron is a fascinating geometric shape with a symmetrical and distinctive structure. Its properties make it an important element in geometry and various other fields of study and application.
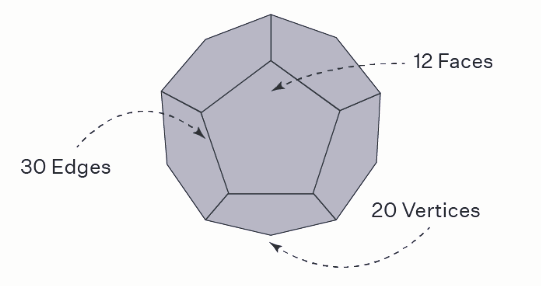
Dodecahedron
A dodecahedron is one of the Platonic solids with distinct properties:
Faces, Edges, and Vertices:
A dodecahedron has 12 pentagonal faces, meaning it consists of 12 sides, each in the shape of a regular pentagon.
It possesses 30 edges.
There are 20 vertices (corners), where three edges meet at each vertex.
Diagonals:
A dodecahedron has a total of 160 diagonals. Diagonals are line segments connecting non-adjacent vertices within the dodecahedron.
Dodecahedra, with their unique pentagonal faces, are encountered in various real-life situations, such as the Roman dodecahedron and dodecahedron-shaped dice, illustrating their relevance and application in different contexts.
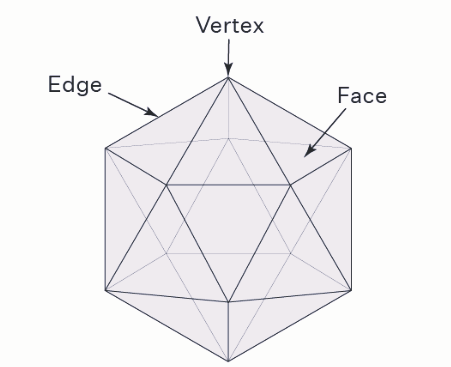
Icosahedron
An icosahedron is another one of the Platonic solids with its own set of properties:
Faces, Edges, and Vertices:
An icosahedron has 20 equilateral triangular faces, which means it consists of 20 sides.
It possesses 30 edges.
There are 12 vertices (corners), where five edges meet at each vertex.
Triangular Faces:
All 20 faces of an icosahedron are in the shape of equilateral triangles. This means that all sides of these triangles are of equal length, and all angles within these triangles are equal.
The icosahedron is a distinctive geometric solid known for its 20 triangular faces and the symmetrical arrangement of its vertices and edges. Its properties make it a fundamental shape in geometry and are relevant in various applications and studies.
Proof of Existence of 5 Platonic Solids
Platonic solids are indeed limited to five unique shapes, and there are mathematical reasons for this limitation:
Vertex Connectivity: For each of the five Platonic solids, at least three faces meet at each vertex. This high degree of connectivity is a key characteristic of Platonic solids and contributes to their geometric stability and symmetry.
Vertex Angles: The internal angles that meet at a vertex in these solids are less than 360 degrees. This angular constraint is a result of the regular and congruent polygons that make up the faces of Platonic solids. In contrast, more complex polyhedra with irregular or non-congruent faces would have internal angles exceeding 360 degrees at their vertices, which is mathematically inconsistent.
Flattening at 360 Degrees: All five Platonic solids have a unique property where their faces flatten out to a full 360 degrees, making them tessellate perfectly without overlaps or gaps. This is due to the fact that the interior angles of the regular polygons forming the faces are such that they can be assembled together seamlessly.
These mathematical constraints, combined with the requirement for regularity and symmetry, limit the number of Platonic solids to just five, setting them apart from other more complex polyhedral shapes.
| Platonic Solid | Meet at Vertex | Angles at Vertex (less than 360°) |
| Tetrahedron | 3 regular triangles meet | Internal angles = 60° 60 × 3 = 180° |
| Cube | 3 squares meet | Internal angles = 90° 90 × 3 = 270° |
| Octahedron | 4 regular triangles meet | Internal angles = 60° 60 × 4 = 240° |
| Dodecahedron | 3 pentagons meet | Internal angles = 108° 108 × 3 = 324° |
| Icosahedron | 5 regular triangles meet | Internal angles = 60° 60 × 5 = 300° |
Euler's Formula for Proof of Existence
Euler's formula correctly to the icosahedron. Euler's formula, which states that F + V - E = 2 for any convex polyhedron, holds true for all such solids, including the icosahedron. In the case of the icosahedron, with 20 faces, 12 vertices, and 30 edges, when you calculate F + V - E, it indeed equals 2:
F + V - E = 20 + 12 - 30 = 2
This equation demonstrates the relationship between the number of faces, vertices, and edges in a polyhedron, and it serves as a fundamental principle in the study of three-dimensional geometry.
| Related Links | |
| Coin Toss Probability Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Platonic Solids Formula FAQs
Q1. What are Platonic Solids?
Q2. What is Euler's Formula and how is it applied to Platonic solids?
Q3. What is the sum of the interior angles at a vertex in Platonic solids?
Q4. Are there any other regular polyhedra besides the five Platonic solids?










