
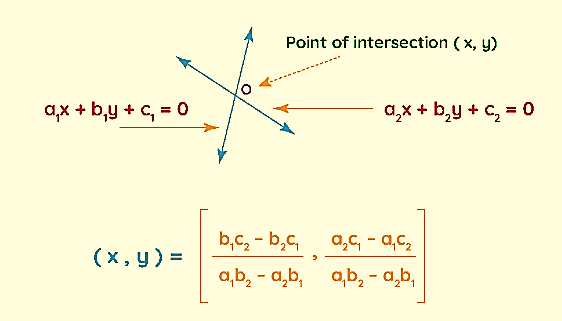
The Point of Intersection Formula is used to find the point where two lines meet, and these two lines can be represented by the equations:
Line 1: a 1 x + b 1 y + c 1 = 0
Line 2: a 2 x + b 2 y + c 2 = 0
What Is the Point of Intersection Formula?
The point of intersection formula is a mathematical method used to find the point at which two lines in a 2D plane intersect. This point is where the two lines cross or meet each other. The formula is based on solving a system of linear equations representing the two lines.
Line 1: a 1 x + b 1 y + c 1 = 0
Line 2: a 2 x + b 2 y + c 2 = 0
The general form of the equations for two lines is as follows:
To find the point of intersection, you typically follow these steps:
Solve one of the equations for one of the variables (usually y or x). This will give you an expression for one variable in terms of the other.
Substitute this expression into the other equation. This results in a single equation with one variable.
Solve this equation for the variable you haven't eliminated.
Once you've found the value of one variable, plug it back into the expression you found in step 1 to determine the value of the other variable.
The solution of this system of equations is the point of intersection (x,y) where the two lines intersect.
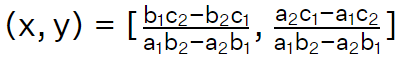
The point of intersection formula is fundamental in geometry, algebra, and other fields where the intersection of lines or curves is relevant. It is used to solve various problems, such as finding the point where two roads intersect, determining where two lines of sight meet, or finding the solution to a pair of linear equations.
Point of Intersection Formula Applications
The point of intersection formula is commonly used in various applications, such as mathematics, engineering, computer graphics, and geography, whenever you need to find the point where two lines intersect in a 2D space. Here are a few practical applications of this formula:
Geometry and Trigonometry: In geometry and trigonometry, the point of intersection formula is used to find the intersection of lines and segments. For example, it can be applied to calculate the intersection of diagonals in a quadrilateral or determine where lines of sight intersect.
Engineering: In engineering, this formula is used to solve problems related to structural design, such as determining the intersection points of beams, cables, or trusses. It is also valuable for navigation, including finding the intersection point of two paths or routes.
Computer Graphics: In computer graphics and game development, this formula is used to determine where lines, vectors, or rays intersect in a 2D space. This is crucial for rendering graphics, simulating physics, and creating visual effects.
Geographical Information Systems (GIS): In GIS, the point of intersection formula is applied to analyze and process geographic data. It can be used to find the intersections of roads, borders, or other geographical features.
Network Routing: In networking and telecommunications, this formula is used to determine the intersection points in a network, helping in routing and optimizing data transmission.
Optics and Light Rays: In optics and physics, this formula helps determine where light rays intersect, which is crucial for designing lenses, mirrors, and optical systems.
Game Development: In game development, this formula is used to calculate collision detection between objects, projectiles, or characters within a game world.
Robotics and Autonomous Vehicles: Autonomous vehicles and robots often use this formula to compute collision avoidance and path planning, ensuring that they do not collide with obstacles.
Surveying: Surveyors use this formula to find the intersection points of lines of sight, essential for accurately measuring distances and angles in land surveying.
Mathematical Problem Solving: The point of intersection formula is fundamental in mathematics and is used to solve systems of linear equations. It has applications in a wide range of mathematical problems, from algebra to calculus.
In each of these applications, the point of intersection formula plays a crucial role in solving problems and making informed decisions, especially when dealing with 2D spatial relationships and line intersections.
Point of Intersection Formula Examples
Example 1:
Let's find the point of intersection of the following two lines:
Line 1: 3x + 2y - 7 = 0
Line 2: 2x - 3y + 5 = 0
Solve Line 1 for y:
2y = -3x + 7
y = (-3/2)x + 7/2
Substitute this expression for y into Line 2:
2x - 3((-3/2)x + 7/2) + 5 = 0
Solve for x:
2x + (9/2)x - 21/2 + 5 = 0
(13/2)x - 21/2 + 5 = 0
(13/2)x - 11/2 = 0
(13/2)x = 11/2
x = (11/13)
Find y using the expression for y:
y = (-3/2)(11/13) + 7/2
y = -33/26 + 91/26
y = 58/26
y = 29/13
So, the point of intersection is (11/13, 29/13).
Example 2:
Let's find the point of intersection of the following two lines:
Line 1: 4x - 5y + 12 = 0
Line 2: 2x + 3y - 6 = 0
Solve Line 1 for y:
-5y = -4x - 12
y = (4/5)x + 12/5
Substitute this expression for y into Line 2:
2x + 3((4/5)x + 12/5) - 6 = 0
Solve for x:
2x + (12/5)x + 36/5 - 6 = 0
(22/5)x + 36/5 - 6 = 0
(22/5)x + 36/5 - 30/5 = 0
(22/5)x + 6/5 = 0
(22/5)x = -6/5
x = (-6/5) * (5/22)
x = -6/22
x = -3/11
Find y using the expression for y:
y = (4/5) * (-3/11) + 12/5
y = -12/55 + 12/5
y = 60/11 - 12/55
y = (300/55) - (12/55)
y = 288/55
So, the point of intersection is (-3/11, 288/55).
| Related Links | |
| Decimal to Fraction Formula | Cost Price Formula |
| Decay Formula | Calculus Formula |
Point of Intersection Formula FAQs
Q1. What is the point of the intersection formula?
Q2. When is the point of intersection formula used?
Q3. How do you find the point of intersection using the formula?
Q4. What are some practical applications of the point of intersection formula?
Q5. Can the point of intersection formula be used for finding the intersection of more than two lines?










