
Quadratic Function Formula: Quadratic functions serve essential roles in various engineering and scientific domains for determining diverse parameters. Visually, they manifest as a parabolic curve. The direction of this curve is determined by the coefficient of the highest degree. The term "quadratic" originates from "quad," signifying "square." Essentially, a quadratic function represents a "polynomial function of degree 2." Their application spans across numerous scenarios, including the depiction of a rocket's trajectory, which follows a quadratic function.
What is Quadratic Function Formula
A quadratic function is a type of polynomial function containing one or more variables where the highest power of the variable is two. As the highest term in a quadratic function is of the second degree, it is referred to as a polynomial of degree 2. Typically, a quadratic function comprises at least one term of the second degree, forming an algebraic function.
The fundamental or parent quadratic function is represented as f(x) = x 2 , linking points whose coordinates follow the pattern (number, number^2). Transformations can be applied to this function, often appearing as f(x) = a(x - h) 2 + k. It can further be manipulated into the form f(x) = ax 2 + bx + c. Each of these forms will be extensively explored in the forthcoming sections for a comprehensive understanding.
Standard Form Quadratic Function Formula
The typical representation of a quadratic function takes the form f(x) = ax 2 + bx + c, where a, b, and c represent real numbers, and a is a non-zero value.

Examples of Quadratic Functions:
f(x)=2x 2 +4x−5; where a=2, b=4, and c=−5.
f(x)=3x 2 −9; where a=3, b=0, and c=−9.
f(x)=x 2 −x; where a=1, b=−1, and c=0.
Now, let's consider f(x)=4x−11; Here, a=0, therefore f(x) is NOT a quadratic function.
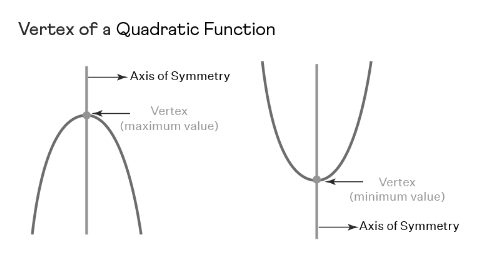
Vertex of Quadratic Function
The vertex of a quadratic function, which typically forms a U shape, signifies the point where the function reaches either its maximum or minimum value. The axis of symmetry of the quadratic function runs through the vertex, intersecting the parabolic curve at that specific point.
Quadratic Function Formula
A quadratic function can often be factored, yet the process might become challenging when dealing with non-integer real or non-real number zeros. In such instances, the quadratic formula serves as a helpful tool to determine these zeroes. The standard form of a quadratic function is expressed as f(x) = ax 2 + bx + c, where a, b, and c represent real numbers and a is not equal to zero. The roots of the quadratic function f(x) can be found using the quadratic formula:
x= [−b± √b 2 −4ac] /2a
Different Types of Quadratic Function
A quadratic function can manifest in various forms: standard form, vertex form, and intercept form. Here are the general representations of each:
Standard form: f(x)=ax 2 +bx+c, where a ≠ 0.
Vertex form: f(x)=a(x−h) 2 +k, where a ≠ 0 (h,k) denotes the vertex of the parabola depicting the quadratic function.
Intercept form: f(x)=a(x−p)(x−q), where a ≠ 0 (p,0) and (q,0) represent the x-intercepts of the parabola portraying the quadratic function.
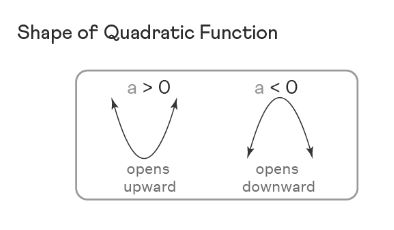
The orientation of the parabola, whether opening upward or downward, depends on the value of 'a': When a>0, the parabola opens upward. When a<0, the parabola opens downward.
One form of a quadratic function can be transformed into another form by straightforwardly simplifying the algebraic expressions. Let's explore the conversion of the standard form into both the vertex form and the intercept form.
Converting Standard Form of Quadratic Function Into Vertex Form
Converting the Standard Form of a Quadratic Function to Vertex Form can be done by using the formulas h = -b/2a and k = f(-b/2a) for a quadratic function f(x) = ax 2 + bx + c. Here's an example:
Example: Let's convert the quadratic function f(x) = 2x 2 - 8x + 3 into the vertex form.
Step 1: Given function: f(x) = 2x 2 - 8x + 3. Compare f(x) = ax 2 + bx + c to determine a = 2, b = -8, and c = 3.
Step 2: Calculate 'h' using the formula: h = -b/2a = -(-8)/2(2) = 2.
Step 3: Determine 'k' using the formula: k = f(-b/2a) = f(2) = 2(2) 2 - 8(2) + 3 = 8 - 16 + 3 = -5.
Step 4: Substitute the values into the vertex form: f(x) = 2(x - 2) 2 - 5.
Converting Standard Form of Quadratic Function Into Intercept Form
To transform the Standard Form of a Quadratic Function into the Intercept Form, you can use the x-intercepts (values p and q) obtained by solving the quadratic equation ax 2 + bx + c = 0. Here's an example:
Example: Converting the quadratic function f(x) = x 2 - 5x + 6 into the intercept form.
Step 1: For the given function f(x) = x 2 - 5x + 6, identify a = 1.
Step 2: Solve the quadratic equation: x 2 - 5x + 6 = 0.
Factoring the left-hand side gives: (x - 3)(x - 2) = 0
The solutions are: x = 3 and x = 2.
Step 3: Substituting the values into the intercept form yields: f(x) = 1(x - 3)(x - 2).
Domain of Quadratic Function
The domain of a quadratic function encompasses all x-values for which the function is defined. As a polynomial function, a quadratic function is defined for all real values of x. Hence, the domain of a quadratic function spans the entire set of real numbers, denoted as R. In interval notation, the domain of any quadratic function is (-∞, ∞).
Range of Quadratic Function
The range of a quadratic function relies on its graph's orientation and the position of its vertex. To determine the range, identify the highest and lowest f(x) values on the function's graph. For a quadratic function with a vertex at (h, k) and an equation in the form f(x) = a(x - h) 2 + k, the range is as follows:
When a > 0 (indicating an upward opening parabola): y ≥ k (or) [k, ∞).
When a < 0 (indicating a downward opening parabola): y ≤ k (or) (-∞, k].
Graphing a Quadratic Function
The graph of a quadratic function takes the shape of a parabola, opening either upwards or downwards in a U-shaped curve. Here are the steps to graph a quadratic function:
Step 1: Determine the vertex.
Step 2: Create a table for the quadratic function with two columns, x and y, including multiple rows (at least five). The table should include the vertex and additional points obtained by choosing values on either side of the vertex.
Step 3: Calculate the corresponding y-values by substituting each x-value into the given quadratic function.
Step 4: Having obtained points on both sides of the vertex, plot these points on a coordinate plane and connect them with a curve, creating the shape of the parabola. Extend the graph on both sides. This constitutes the graph of the quadratic function.
Example: Graphing the quadratic function f(x) = 2x 2 - 8x + 3.
Solution:
Comparing the given function f(x) = 2x 2 - 8x + 3 with f(x) = ax 2 + bx + c, we obtain a = 2, b = -8, and c = 3.
Step 1: Finding the vertex.
x-coordinate of the vertex = -b/2a = 8/4 = 2
y-coordinate of the vertex = f(-b/2a) = 2(2) 2 - 8(2) + 3 = 8 - 16 + 3 = -5.
Hence, the vertex is (2, -5).
Step 2: Create a table with the vertex in the middle row.
Step 3: Fill the first column with arbitrary numbers, one on each side of the x-coordinate, which is 2.
Step 4: Calculate the corresponding y-values by substituting each x-value into the provided quadratic function. For instance, when x = 0, y = 2(0) 2 - 8(0) + 3 = 3.
Step 5: Plot the obtained points on the graph and connect them using a smooth curve.
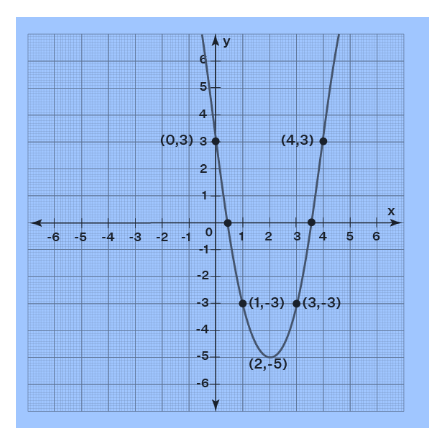
Note: Plotting the x-intercepts and y-intercept of the quadratic function can contribute to refining the graph's shape.
Additionally, quadratic functions' graphs can also be generated using a quadratic functions calculator.
Maxima and Minima of Quadratic Function
Maxima and minima of quadratic functions occur at their respective vertices. These extremities can also be determined using differentiation.
To illustrate this concept, let's consider the example of the quadratic function f(x) = 3x 2 + 4x + 7 and solve it.
By differentiating the function: f ′ (x)=6x+4 Setting the derivative equal to zero:
6x+4=0
x=− 2/3
Upon double differentiation: f ′′ (x)=6>0
Since the second derivative of the function is positive (as per the second derivative test), at x = -2/3, the function exhibits a minimum, and the parabola opens upwards. Conversely, if the second derivative at the stationary point were negative, the function would demonstrate a maximum. Therefore, differentiation provides a means to identify the minimum or maximum of a quadratic function.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Hexagonal Pyramid Formula | Hypothesis Testing Formula |
| Interquartile Range Formula | Inverse Variation Formula |
Quadratic Function Formula FAQs
What is a quadratic function?
How can you find the vertex of a quadratic function?
What is the axis of symmetry of a quadratic function?
How do you determine the roots/zeros of a quadratic function?










