RD Sharma Solutions Class 9 Maths Chapter 4:
In RD Sharma Class 9 Maths Chapter 4, you'll find solutions for algebraic identities. These solutions help explain the problems in the textbook. They make it easier to understand algebraic equations that are always true, no matter the values of the variables. By using these solutions, you can better understand algebraic concepts and how to solve related math problems. They're designed to be easy to follow and help you prepare well for exams.
By using RD Sharma Class 9 Solutions, students can practice important questions for their final exams, improve time management, and enhance logical thinking skills.
These solutions are created by experts at Physics Wallah to help students understand concepts easily. They are available in PDF format for easy access both online and offline.
CBSE Class 9 Science Syllabus 2024-25
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities PDF
Here we have provided RD Sharma Class 9 Solutions Maths Chapter 4 solutions for the students to help them ace their examinations. Students can refer to these solutions and practice these questions to score better in the exams.
RD Sharma Solutions Class 9 Maths Chapter 4 PDF
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1 Page No: 4.6
Question 1: Evaluate each of the following using identities:
(i) (2x – 1/x)
2
(ii) (2x + y) (2x – y)
(iii) (a
2
b – b
2
a)
2
(iv) (a – 0.1) (a + 0.1)
(v) (1.5.x
2
– 0.3y
2
) (1.5x
2
+ 0.3y
2
)
Solution
:
(i)
(2x – 1/x)
2
[Use identity: (a – b)
2
= a
2
+ b
2
– 2ab ]
(2x – 1/x)
2
= (2x)
2
+ (1/x)
2
– 2 (2x)(1/x)
= 4x
2
+ 1/x
2
– 4
(ii)
(2x + y) (2x – y)
[Use identity: (a – b)(a + b) = a
2
– b
2
]
(2x + y) (2x – y) = (2x )
2
– (y)
2
= 4x
2
– y
2
(iii)
(a
2
b – b
2
a)
2
[Use identity: (a – b)
2
= a
2
+ b
2
– 2ab ]
(a
2
b – b
2
a)
2
= (a
2
b)
2
+ (b
2
a)
2
– 2 (a
2
b)( b
2
a)
= a
4
b
2
+ b
4
a
2
– 2 a
3
b
3
(iv)
(a – 0.1) (a + 0.1)
[Use identity: (a – b)(a + b) = a
2
– b
2
]
(a – 0.1) (a + 0.1) = (a)
2
– (0.1)
2
= (a)
2
– 0.01
(v)
(1.5 x
2
– 0.3y
2
) (1.5 x
2
+ 0.3y
2
)
[Use identity: (a – b)(a + b) = a
2
– b
2
]
(1.5 x
2
– 0.3y
2
) (1.5x
2
+ 0.3y
2
) = (1.5 x
2
)
2
– (0.3y
2
)
2
= 2.25 x
4
– 0.09y
4
CBSE Class 10 Result 2024 Expected To Be Out Soon
Question 2: Evaluate each of the following using identities:
(i) (399)
2
(ii) (0.98)
2
(iii) 991 x 1009
(iv) 117 x 83
Solution
:
(i)
(ii)
(iii)
(iv)
Question 3: Simplify each of the following:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
(iv)
Solution
:
(i)
175 x 175 +2 x 175 x 25 + 25 x 25 = (175)
2
+ 2 (175) (25) + (25)
2
= (175 + 25)
2
[Because a
2
+ b
2
+2ab = (a+b)
2
]
= (200)
2
= 40000
So, 175 x 175 +2 x 175 x 25 + 25 x 25 = 40000.
(ii)
322 x 322 – 2 x 322 x 22 + 22 x 22
= (322)
2
– 2 x 322 x 22 + (22)
2
= (322 – 22)
2
[Because a
2
+ b
2
-2ab = (a-b)
2
]
= (300)
2
= 90000
So, 322 x 322 – 2 x 322 x 22 + 22 x 22= 90000.
(iii)
0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
= (0.76)
2
+ 2 x 0.76 x 0.24 + (0.24)
2
= (0.76+0.24)
2
[ Because a
2
+ b
2
+2ab = (a+b)
2
]
= (1.00)
2
= 1
So, 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24 = 1.
(iv)
Question 4: If x + 1/x = 11, find the value of x
2
+1/x
2
.
Solution:
Question 5: If x – 1/x = -1, find the value of x
2
+1/x
2
.
Solution:
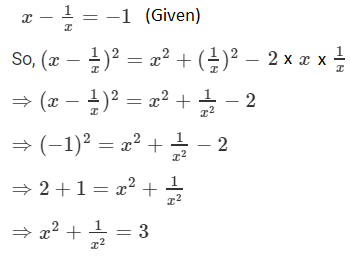
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.2 Page No: 4.11
Question 1: Write the following in the expanded form:
(i) (a + 2b + c)
2
(ii) (2a − 3b − c)
2
(iii) (−3x+y+z)
2
(iv) (m+2n−5p)
2
(v) (2+x−2y)
2
(vi) (a
2
+b
2
+c
2
)
2
(vii) (ab+bc+ca)
2
(viii) (x/y+y/z+z/x)2
(ix) (a/bc + b/ac + c/ab)
2
(x) (x+2y+4z)
2
(xi) (2x−y+z)
2
(xii) (−2x+3y+2z)
2
Solution
:
Using identities:
(x + y + z)
2
= x
2
+ y
2
+ z
2
+ 2xy + 2yz + 2xz
(i)
(a + 2b + c)
2
= a
2
+ (2b)
2
+ c
2
+ 2a(2b) + 2ac + 2(2b)c
= a
2
+ 4b
2
+ c
2
+ 4ab + 2ac + 4bc
(ii)
(2a − 3b − c)
2
= [(2a) + (−3b) + (−c)]
2
= (2a)
2
+ (−3b)
2
+ (−c)
2
+ 2(2a)(−3b) + 2(−3b)(−c) + 2(2a)(−c)
= 4a
2
+ 9b
2
+ c
2
− 12ab + 6bc − 4ca
(iii)
(−3x+y+z)
2
= [(−3x)
2
+ y
2
+ z
2
+ 2(−3x)y + 2yz + 2(−3x)z
= 9x
2
+ y
2
+ z
2
− 6xy + 2yz − 6xz
(iv)
(m+2n−5p)
2
= m
2
+ (2n)
2
+ (−5p)
2
+ 2m × 2n + (2×2n×−5p) + 2m × −5p
= m
2
+ 4n
2
+ 25p
2
+ 4mn − 20np − 10pm
(v)
(2+x−2y)
2
= 2
2
+ x
2
+ (−2y)
2
+ 2(2)(x) + 2(x)(−2y) + 2(2)(−2y)
= 4 + x
2
+ 4y
2
+ 4 x − 4xy − 8y
(vi)
(a
2
+b
2
+c
2
)
2
= (a
2
)
2
+ (b
2
)
2
+ (c
2
)
2
+ 2a
2
b
2
+ 2b
2
c
2
+ 2a
2
c
2
= a
4
+ b
4
+ c
4
+ 2a
2
b
2
+ 2b
2
c
2
+ 2c
2
a
2
(vii)
(ab+bc+ca)
2
= (ab)
2
+ (bc)
2
+ (ca)
2
+ 2(ab)(bc) + 2(bc)(ca) + 2(ab)(ca)
= a
2
b
2
+ b
2
c
2
+ c
2
a
2
+ 2(ac)b
2
+ 2(ab)(c)
2
+ 2(bc)(a)
2
(viii)
(x/y+y/z+z/x)
2
(ix)
(a/bc + b/ac + c/ab)
2
(x)
(x+2y+4z)
2
= x
2
+ (2y)
2
+ (4z)
2
+ (2x)(2y) + 2(2y)(4z) + 2x(4z)
= x
2
+ 4y
2
+ 16z
2
+ 4xy + 16yz + 8xz
(xi)
(2x−y+z)
2
= (2x)
2
+ (−y)
2
+ (z)
2
+ 2(2x)(−y) + 2(−y)(z) + 2(2x)(z)
= 4x
2
+ y
2
+ z
2
− 4xy−2yz+4xz
(xii)
(−2x+3y+2z)
2
= (−2x)
2
+ (3y)
2
+ ( 2z)
2
+ 2(−2x)(3y)+2(3y)(2z)+2(−2x)(2z)
= 4x
2
+ 9y
2
+ 4z
2
−12xy+12yz−8xz
Question 2: Simplify
(i) (a + b + c)
2
+ (a − b + c)
2
(ii) (a + b + c)
2
− (a − b + c)
2
(iii) (a + b + c)
2
+ (a – b + c)
2
+ (a + b − c)
2
(iv) (2x + p − c)
2
− (2x − p + c)
2
(v) (x
2
+ y
2
− z
2
)
2
− (x
2
− y
2
+ z
2
)
2
Solution:
(i)
(a + b + c)
2
+ (a − b + c)
2
= (a
2
+ b
2
+ c
2
+ 2ab+2bc+2ca) + (a
2
+ (−b)
2
+ c
2
−2ab−2bc+2ca)
= 2a
2
+ 2 b
2
+ 2c
2
+ 4ca
(ii)
(a + b + c)
2
− (a − b + c)
2
= (a
2
+ b
2
+ c
2
+ 2ab+2bc+2ca) − (a
2
+ (−b)
2
+ c
2
−2ab−2bc+2ca)
= a
2
+ b
2
+ c
2
+ 2ab + 2bc + 2ca − a
2
− b
2
− c
2
+ 2ab + 2bc − 2ca
= 4ab + 4bc
(iii)
(a + b + c)
2
+ (a – b + c)
2
+ (a + b − c)
2
= a
2
+ b
2
+ c
2
+ 2ab + 2bc + 2ca + (a
2
+ b
2
+ (c)
2
− 2ab − 2cb + 2ca) + (a
2
+ b
2
+ c
2
+ 2ab − 2bc – 2ca)
= 3 a
2
+ 3b
2
+ 3c
2
+ 2ab − 2bc + 2ca
(iv)
(2x + p − c)
2
− (2x − p + c)
2
= [4x
2
+ p
2
+ c
2
+ 4xp − 2pc − 4xc] − [4x
2
+ p
2
+ c
2
− 4xp− 2pc + 4xc]
= 4x
2
+ p
2
+ c
2
+ 4xp − 2pc − 4cx − 4x
2
− p
2
− c
2
+ 4xp + 2pc− 4cx
= 8xp − 8xc
= 8(xp − xc)
(v)
(x
2
+ y
2
− z
2
)
2
− (x
2
− y
2
+ z
2
)
2
= (x
2
+ y
2
+ (−z)
2
)
2
− (x
2
− y
2
+ z
2
)
2
= [x
4
+ y
4
+ z
4
+ 2x
2
y
2
– 2y
2
z
2
– 2x
2
z
2
− [x
4
+ y
4
+ z
4
− 2x
2
y
2
− 2y
2
z
2
+ 2x
2
z
2
]
= 4x
2
y
2
– 4z
2
x
2
Question 3: If a + b + c = 0 and a
2
+ b
2
+ c
2
= 16, find the value of ab + bc + ca.
Solution
:
a + b + c = 0 and a
2
+ b
2
+ c
2
= 16 (given)
Choose a + b + c = 0
Squaring both sides,
(a + b + c)
2
= 0
a
2
+ b
2
+ c
2
+ 2(ab + bc + ca) = 0
16 + 2(ab + bc + c) = 0
2(ab + bc + ca) = -16
ab + bc + ca = -16/2 = -8
or
ab + bc + ca = -8
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3 Page No: 4.19
Question 1: Find the cube of each of the following binomial expressions:
(i) (1/x + y/3)
(ii) (3/x – 2/x
2
)
(iii) (2x + 3/x)
(iv) (4 – 1/3x)
Solution:
[Using identities: (a + b)
3
= a
3
+ b
3
+ 3ab(a + b) and (a – b)
3
= a
3
– b
3
– 3ab(a – b) ]
(i)
(ii)
(iii)
(iv)
Question 2: Simplify each of the following:
(i) (x + 3)
3
+ (x – 3)
3
(ii) (x/2 + y/3)
3
– (x/2 – y/3)
3
(iii) (x + 2/x)
3
+ (x – 2/x)
3
(iv) (2x – 5y)
3
– (2x + 5y)
3
Solution:
[Using identities:
a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)
a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab)
(a + b)(a-b) = a
2
– b
2
(a + b)
2
= a
2
+ b
2
+ 2ab and
(a – b)
2
= a
2
+ b
2
– 2ab]
(i)
(x + 3)
3
+ (x – 3)
3
Here a = (x + 3), b = (x – 3)
(ii)
(x/2 + y/3)
3
– (x/2 – y/3)
3
Here a = (x/2 + y/3) and b = (x/2 – y/3)
(iii)
(x + 2/x)
3
+ (x – 2/x)
3
Here a = (x + 2/x) and b = (x – 2/x)
(iv)
(2x – 5y)
3
– (2x + 5y)
3
Here a = (2x – 5y) and b = 2x + 5y
Question 3: If a + b = 10 and ab = 21, find the value of a
3
+ b
3
.
Solution
:
a + b = 10, ab = 21 (given)
Choose a + b = 10
Cubing both sides,
(a + b)
3
= (10)
3
a
3
+ b
3
+ 3ab(a + b) = 1000
a
3
+ b
3
+ 3 x 21 x 10 = 1000 (using given values)
a
3
+ b
3
+ 630 = 1000
a
3
+ b
3
= 1000 – 630 = 370
or
a
3
+ b
3
= 370
Question 4: If a – b = 4 and ab = 21, find the value of a
3
– b
3
.
Solution
:
a – b = 4, ab= 21 (given)
Choose a – b = 4
Cubing both sides,
(a – b)
3
= (4)
3
a
3
– b
3
– 3ab (a – b) = 64
a
3
– b
3
– 3 × 21 x 4 = 64 (using given values)
a
3
– b
3
– 252 = 64
a
3
– b
3
= 64 + 252
= 316
Or
a
3
– b
3
= 316
Question 5: If x + 1/x = 5, find the value of x
3
+ 1/x
3
.
Solution
:
Given: x + 1/x = 5
Apply Cube on x + 1/x
Question 6: If x – 1/x = 7, find the value of x
3
– 1/x
3
.
Solution
:
Given: x – 1/x = 7
Apply Cube on x – 1/x
Question 7: If x – 1/x = 5, find the value of x
3
– 1/x
3
.
Solution:
Given: x – 1/x = 5
Apply Cube on x – 1/x
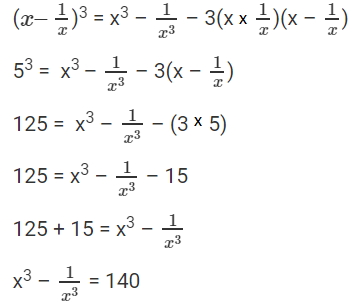
Question 8: If (x
2
+ 1/x
2
) = 51, find the value of x
3
– 1/x
3
.
Solution:
We know that: (x – y)
2
= x
2
+ y
2
– 2xy
Replace y with 1/x, we get
(x – 1/x)
2
= x
2
+ 1/x
2
– 2
Since (x
2
+ 1/x
2
) = 51 (given)
(x – 1/x)
2
= 51 – 2 = 49
or (x – 1/x) = ±7
Now, Find x
3
– 1/x
3
We know that, x
3
– y
3
= (x – y)(x
2
+ y
2
+ xy)
Replace y with 1/x, we get
x
3
– 1/x
3
= (x – 1/x)(x
2
+ 1/x
2
+ 1)
Use (x – 1/x) = 7 and (x
2
+ 1/x
2
) = 51
x
3
– 1/x
3
= 7 x 52 = 364
x
3
– 1/x
3
= 364
Question 9: If (x
2
+ 1/x
2
) = 98, find the value of x
3
+ 1/x
3
.
Solution:
We know that: (x + y)
2
= x
2
+ y
2
+ 2xy
Replace y with 1/x, we get
(x + 1/x)
2
= x
2
+ 1/x
2
+ 2
Since (x
2
+ 1/x
2
) = 98 (given)
(x + 1/x)
2
= 98 + 2 = 100
or (x + 1/x) = ±10
Now, Find x
3
+ 1/x
3
We know that, x
3
+ y
3
= (x + y)(x
2
+ y
2
– xy)
Replace y with 1/x, we get
x
3
+ 1/x
3
= (x + 1/x)(x
2
+ 1/x
2
– 1)
Use (x + 1/x) = 10 and (x
2
+ 1/x
2
) = 98
x
3
+ 1/x
3
= 10 x 97 = 970
x
3
+ 1/x
3
= 970
Question 10: If 2x + 3y = 13 and xy = 6, find the value of 8x
3
+ 27y
3
.
Solution:
Given: 2x + 3y = 13, xy = 6
Cubing 2x + 3y = 13 both sides, we get
(2x + 3y)
3
= (13)
3
(2x)
3
+ (3y)
3
+ 3( 2x )(3y) (2x + 3y) = 2197
8x
3
+ 27y
3
+ 18xy(2x + 3y) = 2197
8x
3
+ 27y
3
+ 18 x 6 x 13 = 2197
8x
3
+ 27y
3
+ 1404 = 2197
8x
3
+ 27y
3
= 2197 – 1404 = 793
8x
3
+ 27y
3
= 793
Question 11: If 3x – 2y= 11 and xy = 12, find the value of 27x
3
– 8y
3
.
Solution:
Given: 3x – 2y = 11 and xy = 12
Cubing 3x – 2y = 11 both sides, we get
(3x – 2y)
3
= (11)
3
(3x)
3
– (2y)
3
– 3 ( 3x)( 2y) (3x – 2y) =1331
27x
3
– 8y
3
– 18xy(3x -2y) =1331
27x
3
– 8y
3
– 18 x 12 x 11 = 1331
27x
3
– 8y
3
– 2376 = 1331
27x
3
– 8y
3
= 1331 + 2376 = 3707
27x
3
– 8y
3
= 3707
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.4 Page No: 4.23
Question 1: Find the following products:
(i) (3x + 2y)(9x
2
– 6xy + 4y
2
)
(ii) (4x – 5y)(16x
2
+ 20xy + 25y
2
)
(iii) (7p
4
+ q)(49p
8
– 7p
4
q + q
2
)
(iv) (x/2 + 2y)(x
2
/4 – xy + 4y
2
)
(v) (3/x – 5/y)(9/x
2
+ 25/y
2
+ 15/xy)
(vi) (3 + 5/x)(9 – 15/x + 25/x
2
)
(vii) (2/x + 3x)(4/x
2
+ 9x
2
– 6)
(viii) (3/x – 2x
2
)(9/x
2
+ 4x
4
– 6x)
(ix) (1 – x)(1 + x + x
2
)
(x) (1 + x)(1 – x + x
2
)
(xi) (x
2
– 1)(x
4
+ x
2
+1)
(xii) (x
3
+ 1)(x
6
– x
3
+ 1)
Solution:
(i)
(3x + 2y)(9x
2
– 6xy + 4y
2
)
= (3x + 2y)[(3x)
2
– (3x)(2y) + (2y)
2
)]
We know, a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)
= (3x)
3
+ (2y)
3
= 27x
3
+ 8y
3
(ii)
(4x – 5y)(16x
2
+ 20xy + 25y
2
)
= (4x – 5y)[(4x)
2
+ (4x)(5y) + (5y)
2
)]
We know, a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab)
= (4x)
3
– (5y)
3
= 64x
3
– 125y
3
(iii)
(7p
4
+ q)(49p
8
– 7p
4
q + q
2
)
= (7p
4
+ q)[(7p
4
)
2
– (7p
4
)(q) + (q)
2
)]
We know, a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)
= (7p
4
)
3
+ (q)
3
= 343 p
12
+ q
3
(iv)
(x/2 + 2y)(x
2
/4 – xy + 4y
2
)
We know,
a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab)
(x/2 + 2y)(x
2
/4 – xy + 4y
2
)
(v)
(3/x – 5/y)(9/x
2
+ 25/y
2
+ 15/xy)
[Using a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab) ]
(vi)
(3 + 5/x)(9 – 15/x + 25/x
2
)
[Using: a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)]
(vii)
(2/x + 3x)(4/x
2
+ 9x
2
– 6)
[Using: a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)]
(viii)
(3/x – 2x
2
)(9/x
2
+ 4x
4
– 6x)
[Using : a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab)]
(ix)
(1 – x)(1 + x + x
2
)
And we know, a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab)
(1 – x)(1 + x + x
2
) can be written as
(1 – x)[(1
2
+ (1)(x)+ x
2
)]
= (1)
3
– (x)
3
= 1 – x
3
(x)
(1 + x)(1 – x + x
2
)
And we know,
a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab)]
(1 + x)(1 – x + x
2
) can be written as,
(1 + x)[(1
2
– (1)(x) + x
2
)]
= (1)
3
+ (x)
3
= 1 + x
3
(xi)
(x
2
– 1)(x
4
+ x
2
+1) can be written as,
(x
2
– 1)[(x
2
)
2
– 1
2
+ (x
2
)(1)]
= (x
2
)
3
– 1
3
= x
6
– 1
[using a
3
– b
3
= (a – b)(a
2
+ b
2
+ ab) ]
(xii)
(x
3
+ 1)(x
6
– x
3
+ 1) can be written as,
(x
3
+ 1)[(x
3
)
2
– (x
3
)(1) + 1
2
]
= (x
3
)
3
+ 1
3
= x
9
+ 1
[using a
3
+ b
3
= (a + b)(a
2
+ b
2
– ab) ]
Question 2: If x = 3 and y = -1, find the values of each of the following using in identity:
(i) (9y
2
– 4x
2
)(81y
4
+ 36x
2
y
2
+ 16x
4
)
(ii) (3/x – x/3)(x
2
/9 + 9/x
2
+ 1)
(iii) (x/7 + y/3)(x
2
/49 + y
2
/9 – xy/21)
(iv) (x/4 – y/3)(x
2
/16 + xy/12 + y
2
/9)
(v) (5/x + 5x)(25/x
2
– 25 + 25x
2
)
Solution:
(i)
(9y
2
– 4x
2
)(81y
4
+ 36x
2
y
2
+ 16x
4
)
= (9y
2
– 4x
2
) [(9y
2
)
2
+ 9y
2
x 4x
2
+ (4x
2
)
2
]
= (9y
2
)
3
– (4x
2
)
3
= 729 y
6
– 64 x
6
Put x = 3 and y = -1
= 729 – 46656
= – 45927
(ii)
Put x = 3 and y = -1
(3/x – x/3)(x
2
/9 + 9/x
2
+ 1)
(iii)
Put x = 3 and y = -1
(x/7 + y/3)(x
2
/49 + y
2
/9 – xy/21)
(iv)
Put x = 3 and y = -1
(x/4 – y/3)(x
2
/16 + xy/12 + y
2
/9)
(v)
Put x = 3 and y = -1
(5/x + 5x)(25/x
2
– 25 + 25x
2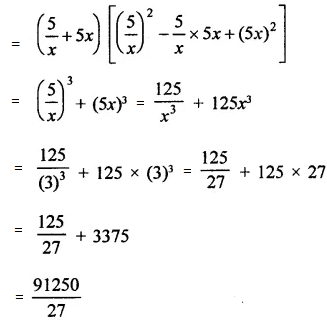
)
Question 3: If a + b = 10 and ab = 16, find the value of a
2
– ab + b
2
and a
2
+ ab + b
2
.
Solution:
a + b = 10, ab = 16
Squaring, a + b = 10, both sides
(a + b)
2
= (10)
2
a
2
+ b
2
+ 2ab = 100
a
2
+ b
2
+ 2 x 16 = 100
a
2
+ b
2
+ 32 = 100
a
2
+ b
2
= 100 – 32 = 68
a
2
+ b
2
= 68
Again, a
2
– ab + b
2
= a
2
+ b
2
– ab = 68 – 16 = 52 and
a
2
+ ab + b
2
= a
2
+ b
2
+ ab = 68 + 16 = 84
Question 4: If a + b = 8 and ab = 6, find the value of a
3
+ b
3
.
Solution:
a + b = 8, ab = 6
Cubing, a + b = 8, both sides, we get
(a + b)
3
= (8)
3
a
3
+ b
3
+ 3ab(a + b) = 512
a
3
+ b
3
+ 3 x 6 x 8 = 512
a
3
+ b
3
+ 144 = 512
a
3
+ b
3
= 512 – 144 = 368
a
3
+ b
3
= 368
RD Sharma Class 9 Solutions Maths Chapter 4 Algebraic Identities Exercise 4.5 Page No: 4.28
Question 1: Find the following products:
(i) (3x + 2y + 2z) (9x
2
+ 4y
2
+ 4z
2
– 6xy – 4yz – 6zx)
(ii) (4x – 3y + 2z) (16x
2
+ 9y
2
+ 4z
2
+ 12xy + 6yz – 8zx)
(iii) (2a – 3b – 2c) (4a
2
+ 9b
2
+ 4c
2
+ 6ab – 6bc + 4ca)
(iv) (3x -4y + 5z) (9x
2
+ 16y
2
+ 25z
2
+ 12xy- 15zx + 20yz)
Solution:
(i)
(3x + 2y + 2z) (9x
2
+ 4y
2
+ 4z
2
– 6xy – 4yz – 6zx)
= (3x + 2y + 2z) [(3x)
2
+ (2y)
2
+ (2z)
2
– 3x x 2y – 2y x 2z – 2z x 3x]
= (3x)
3
+ (2y)
3
+ (2z)
3
– 3 x 3x x 2y x 2z
= 27x
3
+ 8y
3
+ 8Z
3
– 36xyz
(ii)
(4x – 3y + 2z) (16x
2
+ 9y
2
+ 4z
2
+ 12xy + 6yz – 8zx)
= (4x -3y + 2z) [(4x)
2
+ (-3y)
2
+ (2z)
2
– 4x x (-3y) – (-3y) x (2z) – (2z x 4x)]
= (4x)
3
+ (-3y)
3
+ (2z)
3
– 3 x 4x x (-3y) x (2z)
= 64x
3
– 27y
3
+ 8z
3
+ 72xyz
(iii)
(2a -3b- 2c) (4a
2
+ 9b
2
+ 4c
2
+ 6ab – 6bc + 4ca)
= (2a -3b- 2c) [(2a)
2
+ (-3b)
2
+ (-2c)
2
– 2a x (-3b) – (-3b) x (-2c) – (-2c) x 2a]
= (2a)
3
+ (-3b)
3
+ (-2c)
3
-3x 2a x (-3 b) (-2c)
= 8a
3
– 21b
3
– 8c
3
– 36abc
(iv)
(3x – 4y + 5z) (9x
2
+ 16y
2
+ 25z
2
+ 12xy – 15zx + 20yz)
= [3x + (-4y) + 5z] [(3x)
2
+ (-4y)
2
+ (5z)
2
– 3x x (-4y) -(-4y) (5z) – 5z x 3x]
= (3x)
3
+ (-4y)
3
+ (5z)
3
– 3 x 3x x (-4y) (5z)
= 27x
3
– 64y
3
+ 125z
3
+ 180xyz
Question 2: If x + y + z = 8 and xy + yz+ zx = 20, find the value of x
3
+ y
3
+ z
3
– 3xyz.
Solution:
We know, x
3
+ y
3
+ z
3
– 3xyz = (x + y + z) (x
2
+ y
2
+ z
2
– xy – yz – zx)
Squaring, x + y + z = 8 both sides, we get
(x + y + z)
2
= (8)
2
x
2
+ y
2
+ z
2
+ 2(xy + yz + zx) = 64
x
2
+ y
2
+ z
2
+ 2 x 20 = 64
x
2
+ y
2
+ z
2
+ 40 = 64
x
2
+ y
2
+ z
2
= 24
Now,
x
3
+ y
3
+ z
3
– 3xyz = (x + y + z) [x
2
+ y
2
+ z
2
– (xy + yz + zx)]
= 8(24 – 20)
= 8 x 4
= 32
⇒ x
3
+ y
3
+ z
3
– 3xyz = 32
Question 3: If a +b + c = 9 and ab + bc + ca = 26, find the value of a
3
+ b
3
+ c
3
– 3abc.
Solution:
a + b + c = 9, ab + bc + ca = 26
Squaring, a + b + c = 9 both sides, we get
(a + b + c)
2
= (9)
2
a
2
+ b
2
+ c
2
+ 2 (ab + bc + ca) = 81
a
2
+ b
2
+ c
2
+ 2 x 26 = 81
a
2
+ b
2
+ c
2
+ 52 = 81
a
2
+ b
2
+ c
2
= 29
Now, a
3
+ b
3
+ c
3
– 3abc = (a + b + c) [(a
2
+ b
2
+ c
2
– (ab + bc + ca)]
= 9[29 – 26]
= 9 x 3
= 27
⇒ a
3
+ b
3
+ c
3
– 3abc = 27
RD Sharma Class 9 Solutions Maths Chapter 4 Algebraic Identities Exercise VSAQs Page No: 4.28
Question 1: If x + 1/x = 3, then find the value of x
2
+ 1/x
2
.
Solution:
x + 1/x = 3
Squaring both sides, we have
(x + 1/x)
2
= 3
2
x
2
+ 1/x
2
+ 2 = 9
x
2
+ 1/x
2
= 9 – 2 = 7
Question 2: If x + 1/x = 3, then find the value of x^6 + 1/x^6.
Solution
:
x + 1/x = 3
Squaring both sides, we have
(x + 1/x)
2
= 3
2
x
2
+ 1/x
2
+ 2 = 9
x
2
+ 1/x
2
= 9 – 2 = 7
x
2
+ 1/x
2
= 7 …(1)
Cubing equation (1) both sides,
Question 3: If a + b = 7 and ab = 12, find the value of a
2
+ b
2
.
Solution:
a + b = 7, ab = 12
Squaring, a + b = 7, both sides,
(a + b)
2
= (7)
2
a
2
+ b
2
+ 2ab = 49
a
2
+ b
2
+ 2 x 12 = 49
a
2
+ b
2
+ 24 = 49
a
2
+ b
2
= 25
Question 4: If a – b = 5 and ab = 12, find the value of a
2
+ b
2
.
Solution:
a – b = 5, ab = 12
Squaring, a – b = 5, both sides,
(a – b)
2
= (5)
2
a
2
+ b
2
– 2ab = 25
a
2
+ b
2
– 2 x 12 = 25
a
2
+ b
2
– 24 = 25
a
2
+ b
2
= 49
