
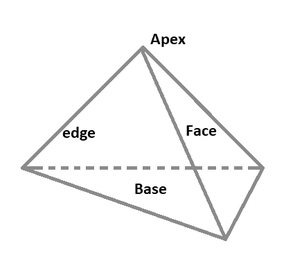
Regular Tetrahedron Formula: A regular tetrahedron consists of four equilateral triangular faces, all of which are identical and congruent to one another. This three-dimensional figure, also termed a triangular pyramid, comprises 4 faces, 6 edges, and 4 vertices. It's depicted in the figure below.
Formula for the Area of One Face of a Regular Tetrahedron
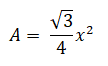
Here, 'x' represents the side length of a regular tetrahedron.
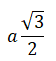
Height on the slant of a Regular Tetrahedron
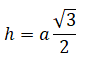
Here, 'a' stands for the base of the triangular face.
The height of a Regular Tetrahedron
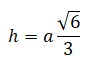
Here, 'a' represents the base of the triangular face.
The formula for the Total Surface Area of a Regular Tetrahedron:
As a regular tetrahedron consists of four identical equilateral triangles, its total surface area is the combined sum of these individual areas. The area of an equilateral triangle with a side length 'x' is calculated as follows:
Area of equilateral triangle =√3x²
Total surface area of regular tetrahedron TSA = 4*√3x²
where x is the length of the side of a regular tetrahedron.
Volume
V =(a³√2) / 12
where x is the length of the side of a regular tetrahedron.
Regular Tetrahedron Formula Solved Examples
Example 1: Find the Total Surface Area (TSA) of a tetrahedron with a side length of 4 cm.
Solution:
TSA of a tetrahedron = √3x²
Here, x = 4 cm
⇒ TSA = √3 x (4)²
= 27.712 cm²
Example 2: Determine the volume of a tetrahedron with a side length of 10 cm.
Solution:
Volume of a tetrahedron = (a³√2) / 12
Here, a = 10 cm
⇒ V = (10³√2) / 12
= 117.85 cm³
Example 3: Compute the Total Surface Area (TSA) of a tetrahedron with a side length of 10 cm.
Solution:
TSA of a tetrahedron = √3x²
Here, x = 10 cm
⇒ TSA = √3 x (10)²
= 173.20 cm²
Example 4: Calculate the Total Surface Area (TSA) of a tetrahedron with a side length of 30 cm.
Solution:
TSA of a tetrahedron = √3x²
Here, x = 30 cm
⇒ TSA = √3 x (30)²
= 1558.84 cm²
Example 5: Determine the volume of a tetrahedron with a side length of 20 cm.
Solution:
Volume of a tetrahedron = (a³√2) / 12
Here, a = 20 cm
⇒ V = (20³√2) / 12
= 942.809 cm³
Example 6: Calculate the volume of a tetrahedron with a side length of 50 cm.
Solution:
Volume of a tetrahedron = (a³√2) / 12
Here, a = 50 cm
⇒ V = (50³√2) / 12
= 14731.39 cm³
Example 7: Calculate the Total Surface Area (TSA) of a regular tetrahedron with a side length of 15 cm.
Solution: The formula for the Total Surface Area (TSA) of a regular tetrahedron is given as: √3x²
Given that x = 15 cm, Substitute the value into the formula:
√3×( 15 ) 2
TSA= √3 ×(15) 2
TSA= √3 ×225
TSA≈389.71cm 2
Example 8: Find the volume of a regular tetrahedron with a side length of 12 cm.
Solution: The formula for the volume of a regular tetrahedron is (a³√2) / 12 .
Given that a = 12 cm, Substitute the value into the formula: (12³√2) / 12
V= 12³√2) / 12
V= 1728 √2 / 12
V≈144 cm 3
The regular tetrahedron, a three-dimensional figure, is composed of four identical equilateral triangular faces, forming a triangular pyramid. It comprises 4 faces, 6 edges, and 4 vertices.
Formulas related to the regular tetrahedron:
Area of One Face: The area of a single face is given by the formula Area of an equilateral triangle = √3x² , where 'x' represents the side length of the tetrahedron.
Slant Height: Denoted by 'a', it signifies the base of the triangular face. Altitude: 'a' is the height of the tetrahedron, which coincides with the base of the triangular face.
Total Surface Area (TSA): The total surface area of the tetrahedron is calculated as TSA=4*√3x², with 'x' representing the side length.
Volume: The volume formula for the tetrahedron is V= (a³√2) / 12 , where 'a' signifies the side length.
Understanding these formulas allows for the precise calculation of the surface area and volume of a regular tetrahedron based on the given side lengths. These calculations prove valuable in geometry and engineering when dealing with triangular-based pyramids.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.
| Related Links | |
| Function Notation Formula | Hexagonal Pyramid Formula |
| Hypothesis Testing Formula | Interquartile Range Formula |
Regular Tetrahedron Formula FAQs
What is a regular tetrahedron?
What is the formula for the area of one face of a regular tetrahedron?
What does 'a' represent in a regular tetrahedron?
How is the total surface area (TSA) of a regular tetrahedron calculated?
What is the formula for the volume of a regular tetrahedron?










