
Resistivity Formula: When an object (conductor) experiences a potential difference, it initiates the movement of electrons, generating a current within the object. As these electrons move, they encounter collisions with other electrons, resulting in resistance to the electron flow. This resistance to the electron movement is termed as Resistance (R), measured in the SI unit ohm (Ω).
Factors Affecting the Resistance
The resistance (R) of a conductor exhibits a direct correlation to the length (l) of the conductor as expressed in (1). Simultaneously, when the conductor maintains a uniform shape, its resistance is inversely proportional to the area of its cross-section, as illustrated in (2).
The nature of the conductor and its temperature significantly impact the overall resistance of the conductor. Combining equations (1) and (2) reveals the relationship R ∝ l/A.
Expressed as the formula R = ρl/A, where ρ (rho) represents the constant term resistivity.
Resistivity Formula
Resistivity, denoted by the symbol ρ (rho), characterizes the inherent property of a material, indicating its capability to either impede or facilitate the flow of electric current. It quantifies the resistance of a material based on both the length and cross-sectional area at a specific temperature.
Another expression of resistivity is given by the formula ρ = (RA)/l, where 'R' signifies resistance, 'A' represents the cross-sectional area, and 'l' denotes the length.
Additionally, resistivity can be represented as Resistivity Formula ρ = 1/σ, where σ stands for conductivity.
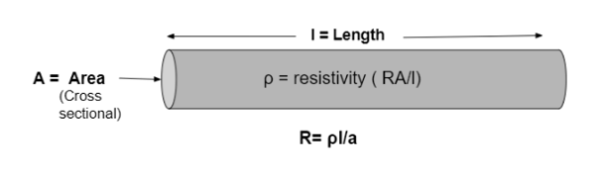
Derivation of Resistivity
We start with the given equation: R = ρl/A
In this equation:
R represents Resistance,
ρ stands for Resistivity,
l is the length of the material, and
A indicates the Area of cross-section.
Rearranging the equation yields: RA = ρl
Thus, ρl = RA
Hence, ρ = RA/l
The SI units are:
SI unit of R = ohm (Ω)
SI unit of A = m²
SI unit of l = m
Hence, the SI unit of ρ is (ohm × m²)/m, which simplifies to ohm meter (Ωm).
Therefore, the SI unit of resistivity is 'ohm meter (Ωm)'.
Factors Affecting the Resistivity
The resistivity of a conductor exhibits a direct correlation to its resistance [ρ ∝ R].
Similarly, the resistivity of a conductor demonstrates a direct proportionality to its uniform cross-sectional area [ρ ∝ A].
In contrast, the resistivity of a conductor shows an inverse relationship to its length [ρ ∝ 1/l].
Furthermore, resistivity is also contingent on the material's nature and temperature.
Resistivity Formula Solved Examples
Example 1: A wire with a resistance of 8 ohms has a length of 2 meters and an area of cross-section 0.5 m². Determine its resistivity.
Solution:
Given:
Resistance (R) = 8 ohms
Length (l) = 2 meters
Area of cross-section (A) = 0.5 m²
Using the Resistivity Formula ρ = RA / l:
ρ = (8 × 0.5) / 2 Ωm
ρ = 4 Ωm
Thus, the resistivity of the wire is 4 Ωm.
Example 2: An unknown material has a resistivity of 12 Ωm. Calculate its conductivity.
Solution:
Given:
Resistivity (ρ) = 12 Ωm
Using the relationship σ = 1 / ρ:
σ = 1 / 12 Ωm
σ ≈ 0.0833 S/m
Therefore, the conductivity of the material is approximately 0.0833 S/m (Siemens per meter).
Example 3: Given a wire with a resistivity of 20Ω⋅m and an area of 0.4m 2 , calculate the length of the wire if its resistance is 100 ohms.
Solution: Given: Resistivity (ρ) = 20 Ω ⋅ m Area (A) = 0.4 m 2 Resistance (R) = 100 ohms
Using the formula R=ρ× l/A , rearrange it to solve for the length
l= 100Ω×0.4m 2 / 20Ω⋅m
l=2m
Hence, the length of the wire is 2m.
| Related Links | |
| Thermal Expansion Formula | Hookes Law Formula |
| Spring Force Formula | Doppler Shift Formula |
Resistivity Formula FAQs
What is resistivity?
How is resistivity calculated?
What factors affect resistivity?
What is the relationship between resistivity and conductivity?
What are the SI units of resistivity?










