Spring Force Formula: Definition, Applications, Solved Examples

Spring Force Formula : Springs are commonly encountered in our daily lives, and understanding the Spring Force Formula is crucial for engineers, physicists, and anyone interested in mechanics. The Spring Force Formula is directly proportional to the displacement from the equilibrium position and follows Hooke's law, which states that the Spring Force Formula is directly proportional to the displacement.

Definition of Spring Force Formula

Spring Force Formula: Spring force, also known as the force exerted by a spring or Hooke's law, is a fundamental concept in physics and engineering. It describes the Spring Force Formula - the force required to compress or extend a spring from its equilibrium position. The Spring Force Formula is directly proportional to the displacement from the equilibrium position and follows Hooke's law, which states that the Spring Force Formula is directly proportional to the displacement. The Spring Force Formula can be expressed as:

F = -k x

Where:

- F is the Spring Force

- k is the Spring Constant (also known as the stiffness constant).

- x is the displacement from the equilibrium position.

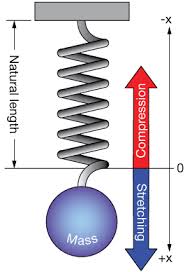
Spring Force Formula

As mentioned earlier, the Formula for the Spring Force Formula is given by:

F = -k * x

This Spring Force Formula tells us that the Spring Force is equal to the negative product of the Spring Constant and the displacement from the equilibrium position. The negative sign indicates that the Spring Force Formula acts in the opposite direction of the displacement. When the Spring Force Formula is compressed, the Spring Force Formula is directed outward, while when it's extended, the Spring Force Formula is directed inward.

Spring Constant (Stiffness Constant)

The Spring Constant, denoted by 'k,' is a measure of the stiffness of the Spring Force. The Spring Constant varies from one Spring Force Formula to another and depends on factors like the material, dimensions, and design of the Spring Force Formula. The higher the Spring Constant, the stiffer the Spring Force Formula and the more force is required to produce a given displacement.

Also Check – Voltage Drop Formula

Applications of the Spring Force Formula

The Spring Force  finds applications in various fields:

1. Mechanical Engineering: Springs are used in suspension systems, shock absorbers, and more.
2. Physics: Understanding the Spring Force Formula is crucial in studying mechanical oscillations and waves.
3. Consumer Products: Springs are used in everyday items like mattresses, trampolines, and door hinges.
4. Civil Engineering: In construction, springs are used in structures to absorb seismic forces
5. Medical Devices: Springs play a role in designing medical equipment like syringes and prosthetic limbs.

Also Check – Electric Field Formula

Solved Examples of the Spring Force Formula

Let's go through a few solved examples to understand how to use the Spring Force Formula in practical scenarios.

Example 1: Suppose you have a Spring Force Formula with a Spring Constant of 500 N/m, and you compress it by 0.2 meters from its equilibrium position. Calculate the Spring Force Formula using the Spring Force Formula.

Solution:

Using the Spring Force Formula:

Spring Force Formula: F = -k * x

F = -500 N/m * 0.2 m

F = -100 N

So, the Spring Force Formula is -100 N. The negative sign indicates that the Spring Force Formula is directed outward.

Example 2: Now, consider a different scenario. You have an extended Spring Force Formula with a Spring Constant of 800 N/m, and you compress it by 0.15 meters from its equilibrium position. Calculate the Spring Force Formula using the Spring Force Formula.

Solution:

Again, using the Spring Force Formula:

Spring Force Formula: F = -k * x

F = -800 N/m * 0.15 m

F = -120 N

In this case, the Spring Force Formula is -120 N, indicating that it's directed inward.

Example 3: You have a spring with a Spring Constant of 1000 N/m. If the spring is compressed by 0.1 meters from its equilibrium position, what is the Spring Force?

Solution:

Using the Spring Force Formula:

Spring Force Formula: F = -k * x

F = -1000 N/m * 0.1 m

F = -100 N

The Spring Force is -100 N, directed outward.

Also Check – sound Formula

Example 4: A Spring Force Formula has a Spring Constant of 1500 N/m. If it is extended by 0.25 meters from its equilibrium position, calculate the Spring Force.

Solution:

Using the Spring Force Formula:

Spring Force Formula: F = -k * x

F = -1500 N/m * 0.25 m

F = -375 N

The Spring Force is -375 N, directed inward.

Example 5: Suppose you have a spring with a Spring Constant of 800 N/m. It is compressed by 0.15 meters and then extended by 0.1 meters from the equilibrium position. Calculate the net Spring Force.

Solution:

For the compression:

F_compression = -k * x

F_compression = -800 N/m * 0.15 m

F_compression = -120 N

For the extension:

F_extension = -k * x

F_extension = -800 N/m * 0.1 m

F_extension = -80 N

To find the net Spring Force, subtract the force due to extension from the force due to compression:

Net Spring Force = F_compression - F_extension

Net Spring Force = (-120 N) - (-80 N)

Net Spring Force = -120 N + 80 N

Net Spring Force = -40 N

The net Spring Force is -40 N, directed outward.

Example 6: You have a spring with a Spring Constant of 1200 N/m. If it is extended by 0.3 meters and then compressed by 0.2 meters, calculate the total work done by the Spring Force.

Solution:

To find the total work done by the Spring Force, we need to calculate the work done during extension and compression and then add them together.

Work done during extension:

W_extension = (1/2) * k * x^2

W_extension = (1/2) * 1200 N/m * (0.3 m)^2

W_extension = 54 J

Work done during compression:

W_compression = (1/2) * k * x^2

W_compression = (1/2) * 1200 N/m * (0.2 m)^2

W_compression = 24 J

Total work done by the Spring Force:

Total Work = W_extension + W_compression

Total Work = 54 J + 24 J

Total Work = 78 J

The total work done by the Spring Force is 78 Joules.

Example 7: A spring with a Spring Constant of 600 N/m is compressed by 0.25 meters. Calculate the acceleration of an object with a mass of 2 kg attached to this spring.

Solution:

To find the acceleration of the object, we'll use Newton's second law, which states:

F = m * a

Where:

- F is the force (Spring Force).

- m is the mass of the object.

- a is the acceleration.

We already know the Spring Force using the Spring Force Formula:

Spring Force Formula: F = -k * x

F = -600 N/m * 0.25 m

F = -150 N

Now, we can calculate the acceleration:

-150 N = 2 kg * a

a = (-150 N) / (2 kg)

a = -75 m/s²

The acceleration of the object is -75 m/s², indicating that it's directed opposite to the compression of the spring.