Physics Wallah

Roots of x2-11x-28=0, How to Solve Quadratic Equations? Find Solution

Here we have provided Roots of x2-11x-28=0. Check this article to learn how to Solve Quadratic equations using various methods.
authorImageNeha Tanna10 May, 2024
Share

Share

Roots of x2-11x-28=0

Roots of x2-11x-28=0= Second-degree algebraic expressions in the form ax2 + bx + c = 0 are known as quadratic equations. The word "quadratic," which describes how the variable x is squared in the equation, is derived from the Latin word "quadratus," which means square. Put differently, an "equation of degree 2" is a quadratic equation.

There are numerous situations in which one uses a quadratic equation. Did you know that a quadratic equation can be used to explain the trajectory of a rocket when it is launched? A quadratic equation also has many uses in astronomy, engineering, physics, and other fields. There are two possible solutions to a quadratic equation, and they can both be real or complex integers. These two solutions (values of x) are denoted as (α, β) and are also known as the roots of the quadratic equations. In the content that follows, we will discover more about a quadratic equation's roots.

Question 1:

Find roots of equation x 2 − 11 x + 28 = 0 by quadratic formula.

Solution:

What is Quadratic Equation?

An algebraic equation of the second degree in x is called a quadratic equation. The conventional form of the quadratic equation is ax2 + bx + c = 0, where x is the variable, b and c are the coefficients, and c is the constant factor. The coefficient of x2 must be a non-zero term (a ≠ 0) in order for an equation to be considered quadratic. The x2 term is written first, then the x term, and lastly the constant term when expressing a quadratic equation in standard form.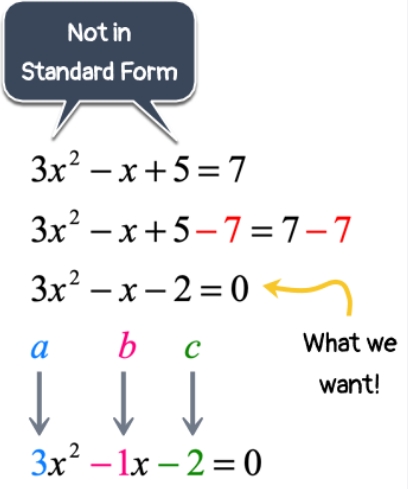

Roots of a Quadratic Equation

When a quadratic equation is solved, the two values of x that result are the problem's roots. The zeros in the equation are another name for these quadratic equation roots. For instance, since both x = -1 and x = 4 satisfy the equation, they are the roots of x2 - 3x - 4 = 0.

Also Check - How many Centimeters are in a Meter?

Quadratic Formula

The simplest method for determining a quadratic equation's roots is to use the quadratic formula. Sometimes it's difficult to factor a quadratic equation; in these cases, we can quickly and simply discover the roots by using this quadratic formula. The quadratic formula's two roots are given as a single statement. To find the two different roots of the equation, one can use either the positive or negative sign.

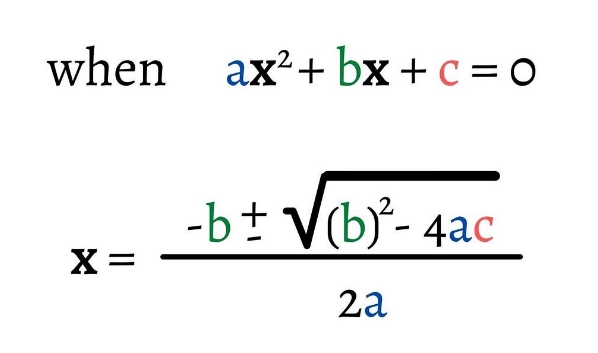
Nature of Roots of the Quadratic Equation

Typically, the symbols alpha (α) and beta (β) are used to indicate the roots of a quadratic equation. In this section, we will explore the process of determining the characteristics of a quadratic equation's roots without actually locating the equation's roots. It is possible to determine the nature of roots of a quadratic equation without actually locating the equation's roots (α, β). This can be accomplished by using the discriminant value, which is a component of the quadratic equation solution formula. 'D' stands for the discriminant of a quadratic equation, which is equal to b2 - 4ac. It is possible to predict the kind of roots of the quadratic equation based on the discriminant value.

Methods to Solve Quadratic Equations

Two values of x or the equation's two roots can be found by solving a quadratic equation. The roots of the quadratic equation can be found using one of four techniques. The following are the four approaches to solve the quadratic equations.
  • Factorizing of Quadratic Equation
  • Using quadratic formula (which we have seen already)
  • Method of Completing the Square
  • Graphing Method to Find the Roots

Solving Quadratic Equations by Factorization

The process of factorising a quadratic equation involves several phases. The middle word must first be divided into two terms so that the sum of the terms equals the constant term in order to obtain a generic form of the quadratic equation ax2 + bx + c = 0. In addition, we can extract the common words from the provided term to ultimately derive the necessary elements in the following way: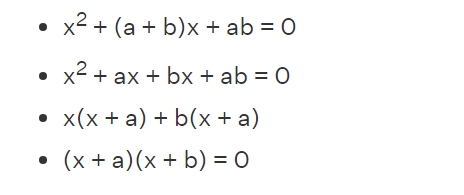
Rational Numbers Formula Linear Equation Formula
Quadrilaterals Formula Line and Angles Formula
Polynomials Formula Arithmetic Progressions Formul

Method of Completing the Square

Completing the square in a quadratic equation involves simplifying and algebraically squaring the problem to find the necessary equation roots. A quadratic equation is as follows: ax2 + bx + c = 0, a ≠ 0. We simplify this equation as follows in order to find its roots:

How to solve a Quadratic Equation involving Modulus

Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.