Physics Wallah

RS Aggarwal Solutions Class 9 Maths Chapter 7 Lines and Angles

Here, we have provided RS Aggarwal Solutions Class 9 Maths Chapter 7. Students can view these RS Aggarwal Solutions Class 9 Maths Chapter 7 before exams for better understanding of the chapter.
authorImageAnanya Gupta11 Apr, 2024
Share

Share

RS Aggarwal Solutions Class 9 Maths Chapter 7

RS Aggarwal Solutions Class 9 Maths Chapter 7: RS Aggarwal Solutions Class 9 Maths Chapter 7 - Lines and Angles is a helpful guide for students learning about lines and angles. In this chapter, you'll learn about different types of angles and properties of lines.

The solutions provided in this guide are easy to follow, with clear explanations for each problem. By practicing with these solutions, you can improve your understanding of geometry and become more confident in solving related problems.

RS Aggarwal Solutions Class 9 Maths Chapter 7 - Lines and Angles PDF

You can access the RS Aggarwal Solutions for Class 9 Maths Chapter 7 - Lines and Angles PDF through the provided link. These solutions provide detailed explanations and step-by-step guidance to help you understand and solve the exercises in your textbook. By using these solutions, you can enhance your understanding of lines and angles, sharpen your problem-solving skills, and prepare effectively for exams.

RS Aggarwal Solutions Class 9 Maths Chapter 7 - Lines and Angles PDF

RS Aggarwal Solutions Class 9 Maths Chapter 7 - Lines and Angles

Below, you'll find detailed solutions for RS Aggarwal Class 9 Maths Chapter 7 - Lines and Angles. These solutions are designed to help you understand the concepts better and solve problems step by step. They'll assist you in improving your problem-solving skills and preparing for exams effectively. Whether you're revising concepts or practicing exercises, these solutions will be a useful resource to support your learning in mathematics.

RS Aggarwal Solutions Class 9 Chapter 7 Lines and Angles Exercise- 4.1

RS Aggarwal Solutions Class 9 Chapter 7 Lines and Angles  Exercise- 4.2

Question 15.

Solution:

Given ∠AOC and ∠BOC are supplementary angles OE is the bisector of ∠BOC and OF is the bisector of ∠AOC To Prove : ∠EOF = 90° Proof : ∠1 = ∠2 ∠3 = ∠4 {OE and OF are the bisectors of ∠BOC and ∠AOC respectively} But ∠AOC + ∠BOC = 180° (Linear pair) => ∠1 + ∠2 + ∠3 + ∠4 = 180° => ∠1 + ∠1 + ∠3 + ∠3 = 180° => 2∠1 + 2∠3 = 180° => 2(∠1 + ∠3) = 180° => ∠1 + ∠3 = 180°/2 = 90° => ∠EOF = 90° Hence proved. RS Aggarwal Solutions Class 9 Chapter 7 Lines and Angles Exercise- 4.3

Question 1.

Solution:

Since AB and CD are given to be parallel lines and t is a transversal. So, ∠5 = ∠1 = 70o [Corresponding angles are equal] ∠3 = ∠1 = 70o [Vertically opp. Angles] ∠3 + ∠6 = 180o [Co-interior angles on same side] ∴ ∠6 = 180o – ∠3 = 180o – 70o = 110o ∠6 = ∠8 [Vertically opp. Angles] ⇒ ∠8 = 110o ⇒ ∠4 + ∠5 = 180o [Co-interior angles on same side] ∠4 = 180o – 70o = 110o ∠2 = ∠4 = 110o [ Vertically opposite angles] ∠5 = ∠7 [Vertically opposite angles] So, ∠7 = 70o ∴ ∠2 = 110o, ∠3 = 70o, ∠4 = 110o, ∠5 = 70o, ∠6 = 110o , ∠7 = 70o and ∠8 = 110o

Question 2.

Solution:

Since ∠2 : ∠1 = 5 : 4. Let ∠2 and ∠1 be 5x and 4x respectively. Now, ∠2 + ∠1 = 180, because ∠2 and ∠1 form a linear pair. So, 5x + 4x = 180o ⇒ 9x = 180o ⇒ x = 20o ∴ ∠1 = 4x = 4 × 20o = 80o And ∠2 = 5x = 5 × 20o = 100o ∠3 = ∠1 = 80o [Vertically opposite angles] And ∠4 = ∠2 = 100o [Vertically opposite angles] ∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles] So, ∠5 = 80o and ∠6 = 100o ∠8 = ∠6 = 100o [Vertically opposite angles] And ∠7 = ∠5 = 80o [Vertically opposite angles] Thus, ∠1 = 80o, ∠2 = 100o, ∠3 = ∠80o, ∠4 = 100o, ∠5 = 80o, ∠6 = 100o ∠7 = 80o and ∠8 = 100o

Question 3.

Solution:

Given: AB || CD and AD || BC To Prove: ∠ADC = ∠ABC Proof: Since AB || CD and AD is a transversal. So sum of consecutive interior angles is 180o . ⇒ ∠BAD + ∠ADC = 180o ....(i) Also, AD || BC and AB is transversal. So, ∠BAD + ∠ABC = 180o ....(ii) From (i) and (ii) we get: ∠BAD + ∠ADC = ∠BAD + ∠ABC ⇒ ∠ADC = ∠ABC (Proved)

Question 4.

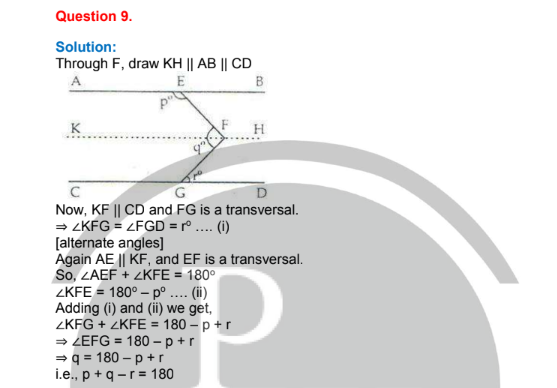
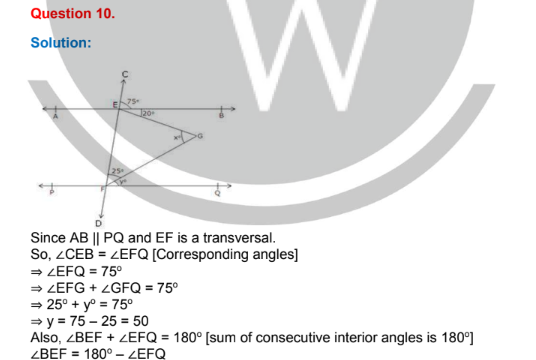
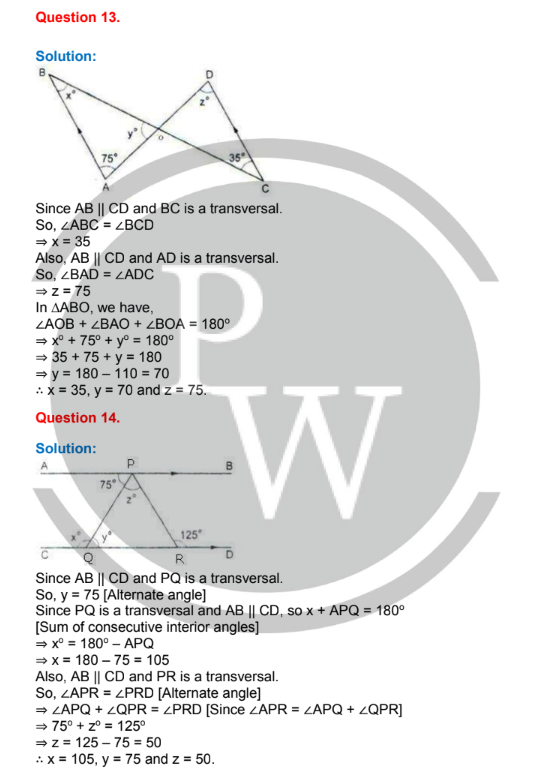
Question 15.

RS Aggarwal Solutions Class 9 Chapter 7 Lines and Angles Exercise- 4.3

Question 1.

Solution:

Since AB and CD are given to be parallel lines and t is a transversal. So, ∠5 = ∠1 = 70o [Corresponding angles are equal] ∠3 = ∠1 = 70o [Vertically opp. Angles] ∠3 + ∠6 = 180o [Co-interior angles on same side] ∴ ∠6 = 180o – ∠3 = 180o – 70o = 110o ∠6 = ∠8 [Vertically opp. Angles] ⇒ ∠8 = 110o ⇒ ∠4 + ∠5 = 180o [Co-interior angles on same side] ∠4 = 180o – 70o = 110o ∠2 = ∠4 = 110o [ Vertically opposite angles] ∠5 = ∠7 [Vertically opposite angles] So, ∠7 = 70o ∴ ∠2 = 110o , ∠3 = 70o , ∠4 = 110o , ∠5 = 70o, ∠6 = 110o , ∠7 = 70o and ∠8 = 110o

Question 2.

Solution:

Since ∠2 : ∠1 = 5 : 4. Let ∠2 and ∠1 be 5x and 4x respectively. Now, ∠2 + ∠1 = 180 because ∠2 and ∠1 form a linear pair. So, 5x + 4x = 180o ⇒ 9x = 180o ⇒ x = 20o ∴ ∠1 = 4x = 4 × 20o = 80o And ∠2 = 5x = 5 × 20o = 100o ∠3 = ∠1 = 80o [Vertically opposite angles] And ∠4 = ∠2 = 100o [Vertically opposite angles] ∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles] So, ∠5 = 80o and ∠6 = 100o ∠8 = ∠6 = 100o [Vertically opposite angles] And ∠7 = ∠5 = 80o [Vertically opposite angles] Thus, ∠1 = 80o , ∠2 = 100o, ∠3 = ∠80o, ∠4 = 100o, ∠5 = 80o, ∠6 = 100o,∠7 = 80o and ∠8 = 100o

Question 13.

Solution:

Question 15.

Benefits of RS Aggarwal Solutions Class 9 Maths Chapter 7 - Lines and Angles

RS Aggarwal Solutions for Class 9 Maths Chapter 7 - Lines and Angles provide several benefits to students:

Detailed Coverage: The solutions cover all the topics and concepts included in the chapter, ensuring a thorough understanding of the subject matter.

Step-by-Step Approach: Each solution is presented in a step-by-step manner, making it easier for students to follow and learn.

Clarity of Concepts: The solutions provide clear explanations and reasoning behind each step, helping students grasp the underlying concepts more effectively.

Practice Material: The solutions include ample practice questions and examples to help students reinforce their learning and improve their problem-solving skills.

Preparation for Exams: By practicing with RS Aggarwal Solutions, students can better prepare for their exams and gain confidence in tackling questions related to lines and angles.

CBSE Class 9 Maths Syllabus CBSE Class 9 Science Syllabus
CBSE Class 9 Computer Application Syllabus CBSE Class 9 Social Science Syllabus

RS Aggarwal Solutions Class 9 Maths Chapter 7 FAQs

How can RS Aggarwal Solutions for Class 9 Maths Chapter 7 help in exam preparation?

RS Aggarwal Solutions provide detailed explanations and step-by-step solutions to all the questions in the textbook. By practicing with these solutions, students can improve their understanding of the concepts and prepare effectively for exams.

Are the solutions provided in RS Aggarwal Solutions easy to understand?

Yes, RS Aggarwal Solutions are designed to be easy to understand. Each solution is presented in a clear and concise manner, with detailed explanations provided for each step. This makes it easier for students to follow along and grasp the concepts.

Can RS Aggarwal Solutions for Class 9 Maths Chapter 7 be used for self-study?

Yes, RS Aggarwal Solutions are suitable for self-study. Students can use these solutions to practice solving problems independently and test their understanding of the concepts covered in the chapter.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.