Solid States
have a definite shape and volume. They can be classified based on their bonding/intermolecular forces: ionic, metallic, covalent, or molecular. The focus in the solid state is usually on crystalline solids, where atoms, ions, or molecules are arranged in a specific pattern.
Crystal Lattices & Unit Cells
The entire crystalline solid can be generated by repeating its smallest portion, known as the unit cell.
Possible Variations in Unit Cells:
Primitive (or simple) Cubic:
Particles are only at the corners.
Body-Centered Cubic (BCC): Particles are at the corners and one in the center. Face-Centered Cubic (FCC): Particles are at the corners and at the center of the faces.
Bravais lattices with their respective axial distances (edge lengths) and axial angle
Cubic (Isometric):
Simple Cubic (Primitive) Edge lengths:
a = b = c
Axial angles:
α = β = γ = 90°
Body-Centered Cubic (BCC) Edge lengths:
a = b = c
Axial angles:
α = β = γ = 90°
Face-Centered Cubic (FCC) Edge lengths:
a = b = c
Axial angles:
α = β = γ = 90°
Tetragonal:
Simple Tetragonal (Primitive) Edge lengths:
a = b ≠ c
Axial angles:
α = β = γ = 90°
Body-Centered Tetragonal Edge lengths:
a = b ≠ c
Axial angles:
α = β = γ = 90°
Orthorhombic:
Simple Orthorhombic (Primitive) Edge lengths:
a ≠ b ≠ c
Axial angles:
α = β = γ = 90°
Body-Centered Orthorhombic Edge lengths:
a ≠ b ≠ c
Axial angles:
α = β = γ = 90°
Face-Centered Orthorhombic Edge lengths:
a ≠ b ≠ c
Axial angles:
α = β = γ = 90°
Base-Centered Orthorhombic Edge lengths:
a ≠ b ≠ c
Axial angles:
α = β = γ = 90°
Hexagonal:
Simple Hexagonal (Primitive) Edge lengths
: a = b ≠ c
Axial angles:
α = β = 90°, γ = 120°
Rhombohedral (Trigonal):
Simple Rhombohedral (Primitive) Edge lengths:
a = b = c
Axial angles:
α = β = γ ≠ 90°
Monoclinic:
Simple Monoclinic (Primitive) Edge lengths:
a ≠ b ≠ c
Axial angles:
α = γ = 90°, β ≠ 90°
Base-Centered Monoclinic Edge lengths:
a ≠ b ≠ c
Axial angles:
α = γ = 90°, β ≠ 90°
Triclinic:
Simple Triclinic (Primitive) Edge lengths
: a ≠ b ≠ c
Axial angles:
α ≠ β ≠ γ ≠ 90°
Bragg's Equation
2dsinθ=nλ
where d is the spacing between planes,
θ is the angle of incidence,
n is an integer, and
λ is the wavelength of incident X-rays
Number of Atoms in a Unit Cell
Primitive:
1 atom (each corner atom shared by 8 cells = 8×1/8=1)
BCC:
2 atoms (1 at center + 8 corner atoms × 1/8= 1+1=2)
FCC:
4 atoms (6 face-centered atoms × 1/2 + 8 corner atoms × 1/8= 3+1=4)
Also Read :
Malic Acid Formula
Voids
In close-packed structures, small gaps or voids exist between the spheres. These voids can be of two types:
Tetrahedral Void:
If a sphere is surrounded by four spheres, a tetrahedral void is formed.
Number of tetrahedral voids = 2N
Octahedral Void:
If a sphere is surrounded by six spheres, an octahedral void is formed.
Number of Octahedral voids = N
Packing Efficiency
For FCC (and HCP):
An FCC structure has 8 corner atoms (each shared by 8 cells) and 6 face-centred atoms (each shared by 2 cells). So, 8×1/8 + 6×1/2 = 4 atoms.
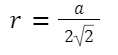
volume of 4 spheres =
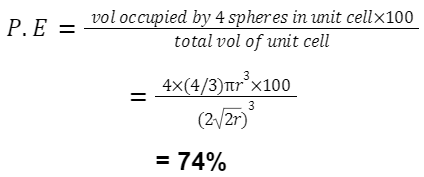
Packing Efficiency in BCC: Atoms per unit cell = 2
Given edge length = a, the radius r can be found using body diagonal = √3a = 4r
.
volume occupied =
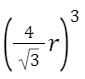
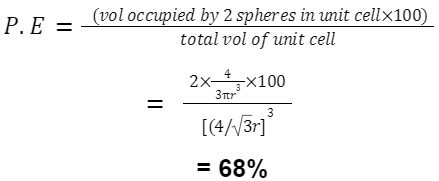
Simple Cubic
:
Atoms per unit cell:
For a cubic system with edge length a, a=2r, where r is the atomic radius.
volume occupied =
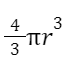
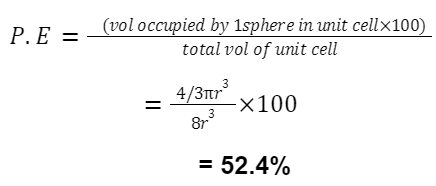
Also Check –
Monatomic Gases Formula
Calculations Involving Unit Cell Dimensions
Simple Cubic (SC):
Atoms per unit cell: 1 Edge length: a=2r, where r is the atomic radius.
Volume of the unit cell: a
3
=(2r)
3
= 8r
3
Body-Centered Cubic (BCC): Atoms per unit cell: 2 Relation between edge length and atomic radius:
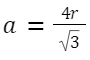
Volume of the unit cell:
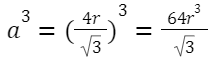
Face-Centered Cubic (FCC):
Atoms per unit cell: 4
Relation between edge length and atomic radius: a =2√2r
Volume of the unit cell:
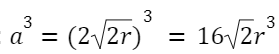
Also Check –
Lead (II) Chloride Formula
Calculations for Other Parameters
Density of the Crystal:
Density (d) = Mass of atoms in the unit cell /Volume of the unit cell
For simple cubic,
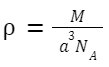
For BCC,
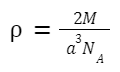
For FCC,
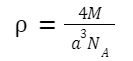
Tetragonal and Orthorhombic Systems:
For the tetragonal and orthorhombic systems, the edge lengths can vary. However, the relationships become less straightforward, and often specific data or additional information is needed to compute atomic radii or other parameters.
