
Surface Area of a Prism: The surface area of a three-dimensional prism depends on the configuration of its base. It is calculated as the sum of the areas of all the faces comprising the prism. Prisms, being polyhedrons, hold flat faces and no curved surfaces.
What is Surface Area of a Prism
The surface area of a prism represents the collective space taken up by its flat faces. Determining the surface area of a prism involves computing the total area encompassed by all the faces of that specific type of prism or summing the areas of all faces (or surfaces) within a three-dimensional space.
Surface Area of a Prism
The surface area of any prism is determined using a standard formula. This total surface area comprises the sum of the lateral surface area and the area of the two flat bases. Let's examine the formula for the surface area of a prism.
The lateral area belongs to the vertical faces of the prism when the bases are positioned facing upwards and downwards. Hence, the lateral surface area of a prism is calculated as the base perimeter multiplied by the height.
The total surface area of a Prism = Lateral surface area of the prism + area of the two bases = (2 × Base Area) + Lateral surface area or (2 × Base Area) + (Base perimeter × height).
Prisms come in various types, each with distinct bases, leading to different formulas for determining their surface areas. Refer to the table below to comprehend the relationship between the surface area and the various types of prisms.
Surface Area of a Prism |
||
| Shape | Base | Surface Area of Prism = (2 × Base Area) + (Base perimeter × height) |
| Triangular Prism | Triangular | Surface area of triangular prism = bh + (s1 + s2 + b)H |
| Square Prism | Square | Surface area of square prism = 2a2 + 4ah |
| Rectangular Prism | Rectangular | Surface area of rectangular prism = 2(lb + bh + lh) |
| Trapezoidal Prism | Trapezoidal | Surface area of trapezoidal prism = h (b + d) + l (a + b + c + d) |
| Pentagonal Prism | Pentagonal | Surface area of pentagonal prism = 5ab + 5bh |
| Hexagonal Prism | Hexagonal | Surface area of hexagonal prism = 6b(a + h) Surface area of regular hexagonal prism = 6ah + 3√3a |
| Octagonal Prism | Octagonal | Surface area of octagonal prism = 4a2 (1 + √2) + 8aH |
We will compute the surface area of the triangular prism depicted below, utilizing the base "b," the height of the prism "h," and the length "L."
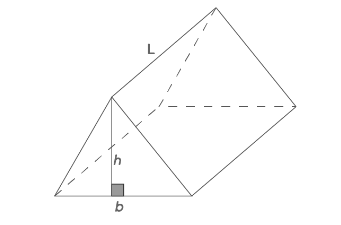
This prism features two triangular bases. Hence, applying the surface area formula for the prism, which is (2 × Base Area) + (Base perimeter × height), considering a triangular base with an area of A = ½ bh and a perimeter of the sum of its sides (a + b + c). Substituting the values into the formula gives us the surface area of a triangular prism as bh + (a + b + c)H = (2A + PH).
Calculating the Surface Area of a Prism
Here's a straightforward guide to finding the surface area of a prism:
Step 1: Note Down the provided dimensions of the prism.
Step 2: Insert these dimensions into the surface area formula for the prism, which is (2 × Base Area) + (Base perimeter × height).
Step 3: The calculated value represents the surface area of the prism, concluding with the unit for the surface area (typically in square units).
Surface Area of a Prism Solved Examples
Example: Determining the Surface Area of a Prism
Given a prism with a base area of 14 square units, a base perimeter of 18 units, and a height of 6 units.
Solution: the surface area is calculated using the formula:
Surface Area of Prism = (2 × Base Area) + (Base perimeter × height)
Given:
Base area = 12 square units
Base perimeter = 18 units
Height of the prism = 6 units
Substituting the values into the formula:
Surface Area of Prism = (2 × 14) + (18 × 6)
S = 136 square units
Hence, the surface area of the prism is 136 square units.
| Related Links | |
| Vertex Formula | Foil Formula |
| Function Notation Formula | Hexagonal Pyramid Formula |
Surface Area of a Prism FAQs
How is the surface area of a prism calculated?
What are the components of the surface area formula for a prism?
Can different types of prisms have unique surface area formulas?
What are some common shapes of prisms and their respective surface area formulas?










